来源:
一、概述
在上一篇文章中我们已经分析了机械臂位姿的描述方法,那么下面就可以正式开始对它进行运动学分析了。
虽然组成机械臂的物件不多,但是它的几何参数还是比较复杂的,各个连杆的长度、关节安装的位置以及传动方式等等,都影响着机械臂末端的位姿变化与关节旋转角度(关节变量)之间的关系。因此,我们首先需要在机械臂的每个连杆上固连一个连杆坐标系,然后,通过描述这些连杆坐标系之间的关系来将末端位姿与关节变量扯上关系,这个关系就是我们想要得到的运动学方程,是以递归的形式得到的。
在对机械臂展开运动学分析前,我们需要一步一步地抽丝剥茧,将实际存在的机械臂抽象为它的运动学模型,如下图所示。

1.1 连杆
机械臂是由一系列刚体通过关节连接而成的运动链,在建立运动学方程时,为了确定机械臂两个相邻关节轴的位置关系,我们将连杆视为刚体,并用空间中的直线来表示关节轴。
首先需要对机械臂的连杆进行编号,我们通常将固定基座定义为连杆0,第一个可动连杆为连杆1,以此类推,机械臂的末端连杆则定义为连杆n,如下图所示。

1.2 关节
两构件通过面接触而构成的运动副称为低副,下图为六种常用的低副关节。
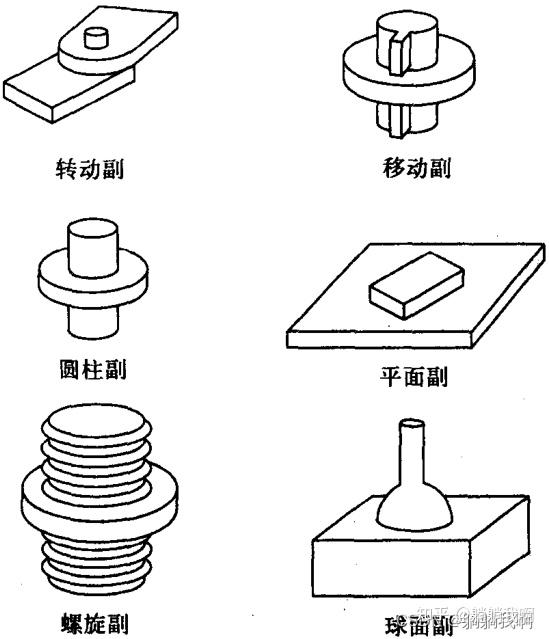
在设计机械臂时,我们通常都会优先选择自由度为一的关节。上图中,转动副与移动副的自由度都是一,分别对应着旋转关节与移动关节,二者常用的表示方法如下图所示。

如下图所示,SCARA机械臂的前三个关节为旋转关节,第四个关节为移动关节。

要注意的是:关节的类型决定了关节变量的类型。
二、Denavit-Hartenberg法

DH法是一种常用的定义连杆坐标系的规则,由J Denavit与RS Hartenberg于1956年提出。其具体规则为:

- 沿着关节i+1的方向选择轴z_i;
- 将原点O_i放置于轴z_i与轴z_i-1和轴z_i的公垂线的交点;
- 将O_i‘放置于公垂线与轴z_i-1的交点;
- 沿着轴z_i-1和z_i的公垂线选择轴x_i,方向由关节i指向关节i+1;
- 最后,选择y_i构成右手系。
当出现下面几种情况时,使用DH法给定的关节坐标系的定义不唯一:
- 对于坐标系0来说,只有轴z_0的方向是指定的,因此,O_0与x_0可以任意选择;
- 对于坐标系n来说(n为机械臂的自由度),由于关节n+1不存在,虽然x_n必须与轴z_n-1垂直,但z_n的定义不唯一。通常,若关节n是转动关节,z_n将按照z_n-1的方向设置;
- 当相邻的两个旋转轴平行时,二者公垂线不唯一;
- 当相邻的两个旋转轴相交时,x_i的方向任意;
- 当关节i为移动型时,z_i-1的方向是任意的。
当出现上述情况时,我们可以采用不明确性来简化过程,例如,相邻的坐标系的轴可定义为平行的。
当我们利用DH法对连杆坐标系完成定义后,会得到4个DH参数,决定了坐标系i关于坐标系i-1的位置和方向:
| 编辑 | Oi 与Oi’ 之间的距离 |
| 编辑 | Oi’ 在连杆坐标系i-1 中的z 坐标 |
| 编辑 | 轴zi 与轴zi-1 之间的夹角 |
| 编辑 | 轴xi 与轴xi-1 之间的夹角 |
这四个参数中,ai 与αi 始终为常数,由连杆之间的机械连接关系决定;剩下的两个参数di 与θi 是否可变由关节的类型决定:若为转动型关节,则θi 为变量;若为移动性关节,则di 为变量。
三、运动学建模
在机械臂的控制过程中我们共定义7个坐标系,前6个为连杆坐标系,且连杆坐标系0 与基坐标系重合,确定它们之间的相对关系可以得出机械臂的DH参数,并可进一步得出齐次变换矩阵;第7个为工具坐标系,是描述末端执行器在基坐标系中位姿的依据。根据机械臂的结构参数最终得出7个坐标系之间的相对位置如下图所示。

其中,坐标系0与基坐标系重合。
机械臂的关节均为转动型,关节变量为θi(1≤i≤6) ,当绕轴zi-1 逆时针旋转时θi 为正。根据上得出机械臂的6组DH参数,如下表所示。
| 连杆编号 | 编辑 | 编辑 | 编辑 | 编辑 | 关节变量范围 |
| 1 | 64.2 | -90 | 169.77 | θ1 | (-170,+170) |
| 2 | 305 | 0 | 0 | θ2 | (-132,0) |
| 3 | 0 | 90 | 0 | θ3 | (1,141) |
| 4 | 0 | -90 | -222.63 | θ4 | (-165,+ 165) |
| 5 | 0 | 90 | 0 | θ5 | (-105,+105) |
| 6 | 0 | 0 | -36.25 | θ6 | (-155,+155) |
DH参数及关节变量范围在构建运动学方程时具有重要作用。





评论0