来源:https://zhuanlan.zhihu.com/p/498346544
一、 冗余机械臂基本概念
1.冗余机械臂的定义
对于机械臂来说,冗余的概念是相对的,是针对具体的任务来定义的,对于一个平面的任务,常用的6轴(六自由度)机械臂也是冗余的。但是更多的情况下,我们采用针对所有任务的情况,因为三维空间能用六个自由度进行描述,我们通常将7轴(七自由度)机械臂称为冗余机械臂。
2.冗余机械臂的优势
我们可以利用冗余机械臂多余的自由度来实现实现本体避障、避奇异、 避关节限位、关节力矩优化、增加操作度等附加任务。同时,由于人的一只胳膊也是有七个自由度,从仿生学的角度,冗余机械臂也比较符合实际。
3.冗余机械臂的构型
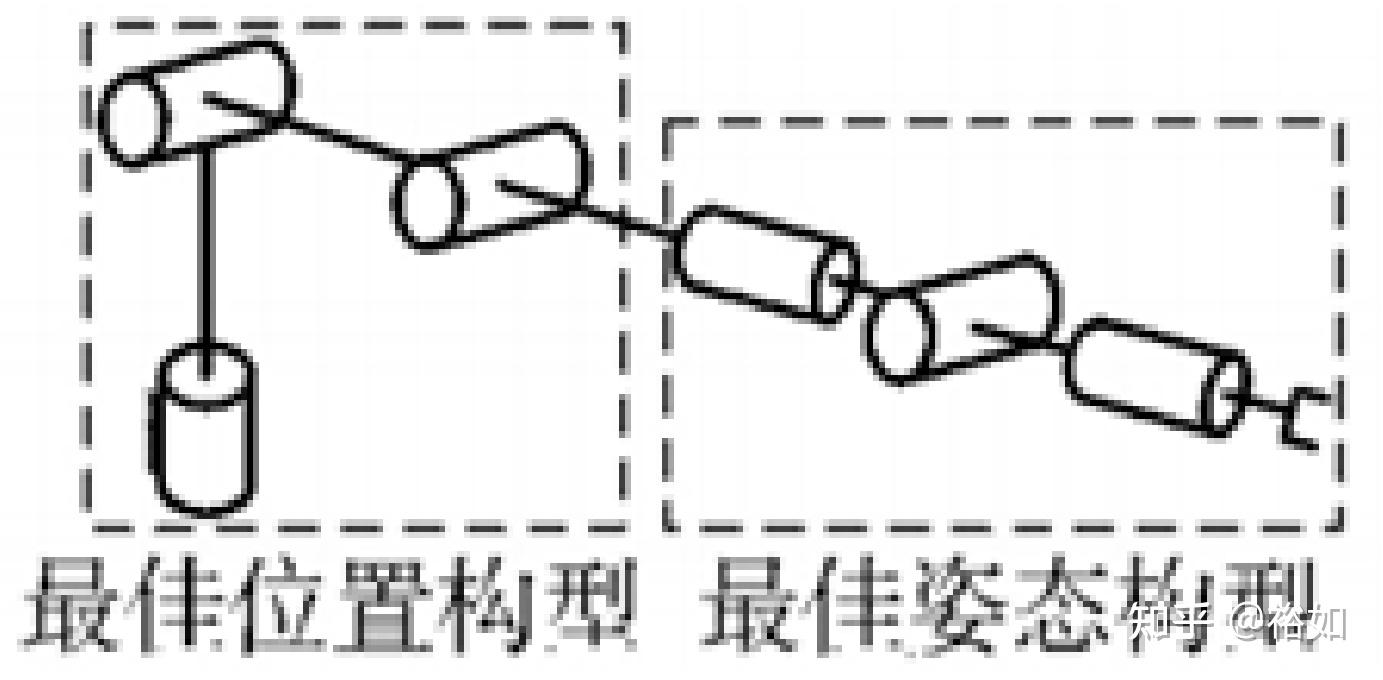
在六自由的最佳构型上,如上图所示,进行加一个轴的操作,可以做出很多种新七轴的构型。
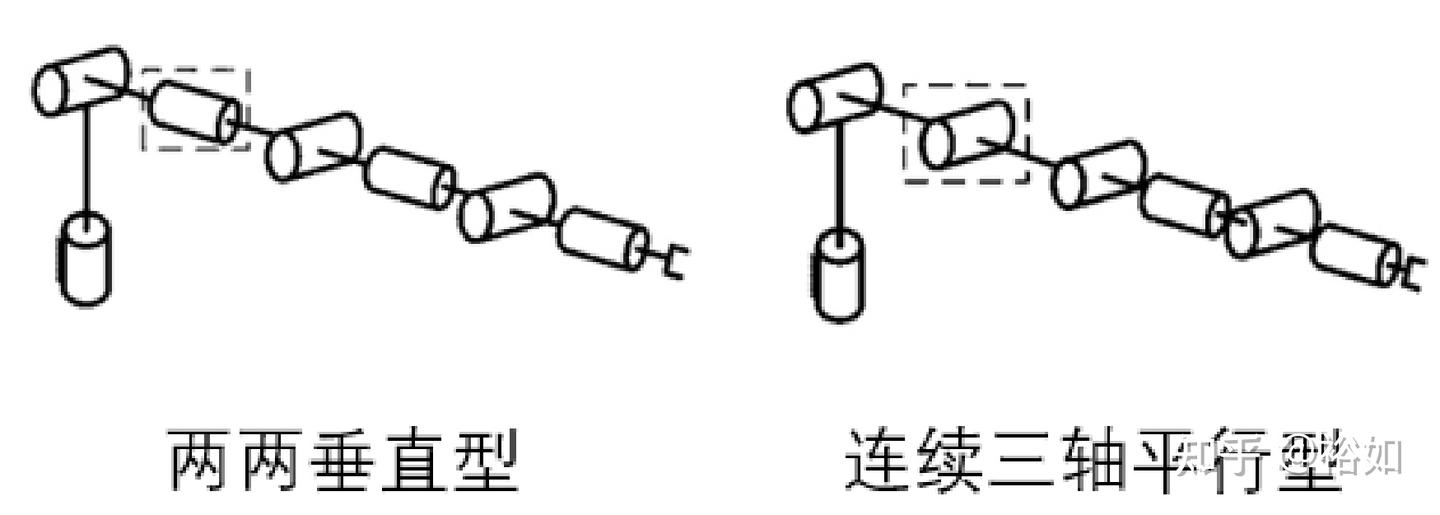
- 两两垂直型(SRS),它是在六自由度构型的二三关节之间加入一个横滚轴得到,形成每相邻两轴互相垂直的关系。
- 连续三轴平行型。它是在六自由度构型的二三关节之间加入一个俯仰轴得到的,会在第二三四关节形成连续三轴平行的关系。
机械臂的构型决定了逆解的方式,本文主要讨论上图第一种符合解析逆解条件的的SRS 构型机械臂。
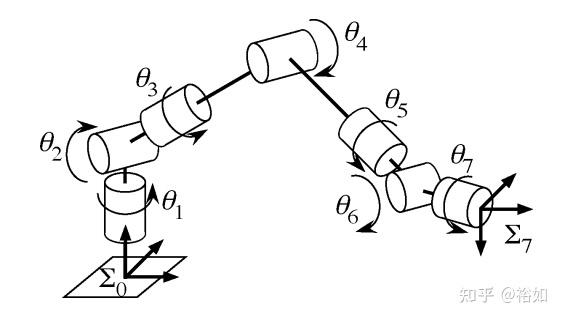
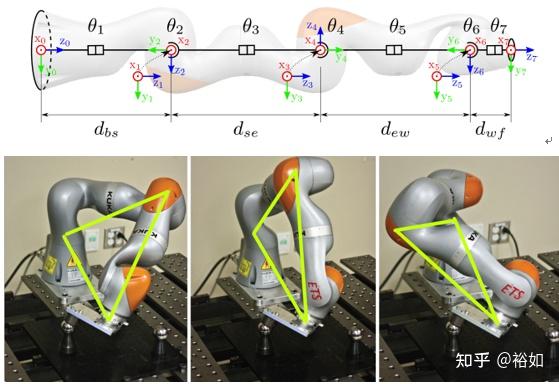
如下图所示,肩关节(1、2和3)可以看作是一个虚拟的球形关节,因为这些关节轴在一个点上相交。肘关节(3、4和5)、腕关节(5、6和7)也有相同的结构。此外,两个相邻的关节轴被垂直放置。
商业化的机械臂中KUKA IIWA采用了这样的构型。
二、冗余机械臂逆解方法
1.冗余机械臂逆解方法的分类
逆运动学解的相关知识点以及分类可以看这篇文章 裕如:机器人的运动学解——逆向运动学解。
冗余机器人运动学逆解的由于其冗余的特点,所以其运动学逆解有无穷多组解。
我们可将方法分为两大类:迭代法和解析法。本文主要围绕着解析法展开。
1)迭代法
逆运动学问题通常是通过线性化一个点周围的构型空间来解决的。即,首先利用由雅可比矩阵表示的线性化的一阶瞬时运动学关系,将逆解问题映射到速度域上,然后在线性化的速度域上寻找瞬时逆解。
对于冗余机械臂,雅可比矩阵有一个零空间,有效利用零空间使我们能够实现各种子任务,如提高可操作度、扭矩优化、避障和奇异回避。这些基于雅可比矩阵的方法可用于跟踪末端执行器的轨迹,该轨迹可以动态生成。
但是,并不适用于分析受关节极限约束的全局构型空间。为了处理关节极限约束下的全局可达区域,我们需要基于位置的解析解法。
2)解析法
需要采用一个待定参数来描述其冗余性,并基于该待定参数解出有限组有效解。通过增加操作空间数或者减少关节自由度数,最终达到操作空间数和关节自由度数相等的情况,从而避免了无穷解的情况。
常用的主要有关节角参数化和臂型角参数化。
关节角参数化:
减少关节待求数,是将其中一个关节变量作为给定参数来代表冗余性,而其他六个关节变量作为待定参数来进行求解,相当于变成了六自由度机械臂运动学逆解问题。
臂型角参数化:
通过增加操作空间数目来达到消除冗余的效果,是把冗余机械臂的冗余度也看作一个描述机械臂的自由度。而且,这个臂型角是可以结合实际应用场景来人为给定的。臂角是衡量机械臂整臂姿态的一个很好的参变量,且由于臂角函数是各个关节角度为自变量,其可以结合机械臂的T矩阵进行位置级别的逆向运动学求解,进而求得其解析解。
2.基于臂型角参数化解析逆运动学求解
2.1 正运动学参数描述
末端的位姿可以通过从基底坐标系观察到的末端坐标系的位置和方向来表示。每个向量/矩阵左侧的上标表示参考坐标系。首先通过DH法,详解见裕如:机器人坐标的描述——D-H参数,建立机械臂的DH参数表,如下图。
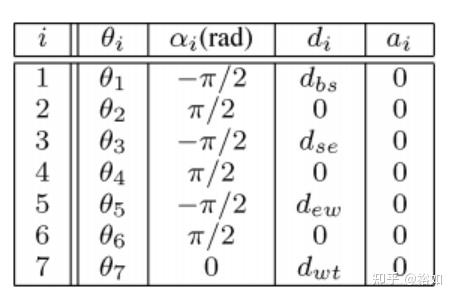
设 0�7∈ℜ3 和 0�7∈��(3) 分别为末端位置和方向。
传统的正向运动学分析提供了关节角度和末端姿态之间的运动学关系
(1)0�7=0���+0�3{3���+3�4(4���+4�77���)}0�7=0�33�44�7
其中 0���,3���,4���,7��� 为常量向量。
(2)0���=[00���]�3���=[0−���0]�4���=[00���]�7���=[00���]�
两坐标系的旋转矩阵为
(3)�−1��=[cos��−sin��cos��sin��sin��sin��cos��cos��−cos��sin��0sin��cos��]
参考平面处的姿态矩阵往往与关节1到3,和关节5到7的旋转矩阵有关。
2.2 臂型角参数与参考平面的确定
冗余机械臂在运动时,因为冗余的存在,当末端位姿确定时, 其关节仍运动的现象叫做机械臂的“自运动”,也被叫做雅可比矩阵零空间的自运动,在零空间(null space)自运动时并不对末端工具的位姿产生影响。
我们在这里用臂型角参数 � 描述这个冗余零空间自运动的参数。
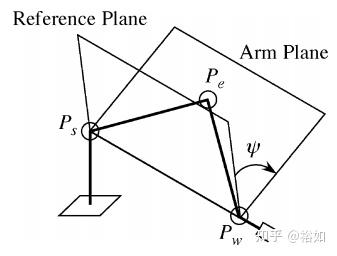
臂型角参数的定义为为目标平面和参考平面的夹角� 。通过臂角参数化七自由度冗余机械臂的自运动, 即若机械臂有自运动现象则其臂平面会相应转动,进而臂角也在改变。
我们首先需要确定一个参考平面。具体方法如下:固定机械臂的关节轴3(用θ3=0表示),当关节轴2和关节轴4平行时,在这种情况下,如果指定了末端执行器的姿态,则臂平面是唯一确定的,由虚拟非冗余机械手提供的臂平面总是可以用作参考平面,我们最终就通过此,以 �0 轴和向量 ��� 确定的参考平面。
2.3 引入罗德里格斯公式的原因
对于S-R-S构型的机械臂的自运动是一个围绕连接肩膀和手腕的轴的旋转。如图4所示,是绕着向量 ��的这个轴在旋转。
设 0���∈�3 是从肩膀指向手腕的向量。
(4)0���=0�7−0���−0�77���
(5)=0�3(3���+3�44���)
如果末端执行器的位置和方向是固定的,那么 0��� 的也是固定的,(4)式中的所有变量都是常数。
因此,对于固定末端执行器位姿的S-R-S机械臂的任何自运动都不会改变相对于基座手腕的位置,而从机械臂基座看的手腕的姿态会根据围绕肩-手腕轴的旋转角度而变化。
由角度� 的旋转引起的方向变化由罗德里格斯公式(Rodrigues’s Formula)得出:
(6)0��=�3+sin�[0���×]+(1−cos�)[0���×]2
其中, �3∈ℜ3×3 为单位矩阵, 0���∈ℜ3 为 0��� 的单位向量, [0���×] 表示向量 0��� 的反对称矩阵。
在已知某向量绕某轴转动一定角度后,根据 罗德里格斯旋转公式 通过向量和转动的角度值可以求得旋转后的向量在坐标系中的旋转矩阵。
由前面已知参考平面是绕向量 �� 进行旋转的,如果知道了参考平面的位姿,在指定一个臂型角之后,就可以求解出参考平面的位姿矩阵绕向量 ��转动臂型角大小后的位姿矩阵。
在求解肩部和腕部的关节角时,其的姿态矩阵与参考平面有关,我们需要利用罗德里格斯公式将对应的姿态矩阵在参考平面下进行描述,如下面的公式(7),这就是罗德里格斯公式的作用。
从基底坐标系中观察到的手腕方向被描述为
(7)0�4=0��0�4�
其中, 0�4� 为臂平面与参考平面重合时的手腕方向。
2.4 肘部关节角的计算
如果指定了末端的姿态,手腕位置是固定的,腕部 3 个关节的运动不改变腕部中心点(即点 W)的位置,肩部 3 个关节的运动不改变肩部中心点(即点 S)的位置。
肘关节角度与参考平面的位置无关,我们可以通过下面的余弦公式(7)唯一的计算出来。
(8)cos�4=‖0���‖2−���2−���22������
�4 有正负两种情况,正负号分别表示肘关节在上或者在下两种结构。
2.5 肩部关节角求解
由于肩关节的角度依赖于参考平面的角度,首先推导出 0�3� 的具体表达式。
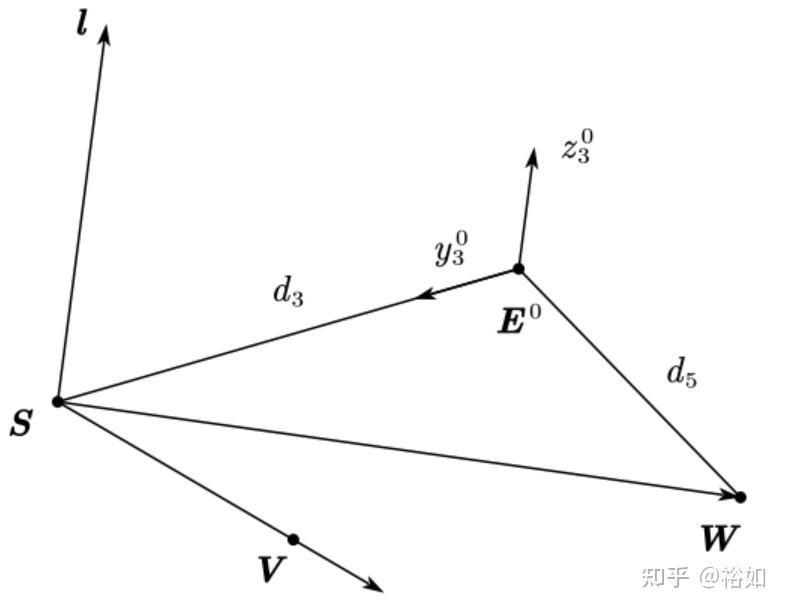
定义参考平面法向量为 �=��×�� ,单位向量表示为 。由图中可知,矢量 ��0 的方向向量可通过矢量��的方向向量绕法向量 � 旋转�角获得
��0=�3�(�,�)��‖��‖
由轴角公式
�(�,�)=Rot(��,�)=�+��×sin�+(��×)2(1−cos�)
其中
��×=[0−���������0−���−������0]
坐标轴 �03 的方向与矢量 ��0 的方向相反,所以可确定 0�03 在{0}坐标系下表示的矢量
0�03=−0��0‖0��0‖
0�30=−sgn(sin�4)⋅0��
根据右手定则可以求得 0�30
0�30=0�30×0�30
可以得到零臂型角下的肘部姿态:
(9)0�30=[0�30,0�30,0�30]
另一种求出 的方法:(待验证)
如前所述,通过将关节角3固定到0来确定参考关节角度。因此,由式(5)推导出,参考肩关节角必须满足该方程
由于肘关节角 由式(7)求出在其它臂型角的情况下, 0�3 的矩阵
(10)0�3=0��0�3�
(6)0��=�3+sin�[0���×]+(1−cos�)[0���×]2
将式(10)与式(6)相消得到下面的公式
(11)0�3=��sin�+��cos�+��
其中
��=[0���×]0�3���=−[0���×]20�3���=[0���0����]0�3�
又根据式(3),我们可以得到旋转矩阵 0�3 为
(12)0�3=[∗−cos�1sin�2∗∗−sin�1sin�2∗−sin�2cos�3−cos�2sin�2sin�3]
将式(11)与式(12)对应项带入,我们可以得到臂角与肩关节角之间的关系,从而求出关节肩部关节1,2,3的角度值
(13)tan�1=−��22sin�−��22cos�−��22−��12sin�−��12cos�−��12
(14)cos�2=−��32sin�−��32cos�−��32
(15)tan�3=��33sin�+��33cos�+��33−��31sin�−��31cos�−��31
2.6 腕部关节角求解
腕关节的求解是通过
(16)4�7=��sin�+��cos�+��
其中
(17)��=3�4����0�7���=3�4����0�7���=3�4����0�7�
关节角1-4的值均已求出,则 0�4为已知量, 然后通过给定的 0�7 ,可得到坐标系{4}到{7}的旋转变换矩阵。
(18)4�7=(0�4)�⋅0�7=[∗∗cos�5sin�6∗∗sin�5sin�6−sin�6cos�7sin�6sin�7cos�6]
将式(16)与式(18)对应项带入,我们可以得到腕角与肩关节角之间的关系,从而求出关节腕部关节5,6,7的角度值
(19)tan�5=��23sin�+��23cos�+��23��13sin�+��13cos�+��13
(20)cos�6=��33sin�+��33cos�+��33
(21)tan�7=��32sin�+��32cos�+��32−��31sin�−��31cos�−��31
至此,七轴机械臂的解析逆解就求解完成了,一般是八组逆解。后期再通过筛选求出最优的一组解。
三、逆解的一些任务拓展
参考文章 Robot-机器人零空间问题solution – 云+社区 – 腾讯云
四步重新认识冗余机器人的控制器设计 – 云+社区 – 腾讯云
基于臂角的逆向运动学,其是机械臂末端位置和姿态控制任务的扩充任务,进而可以填充机械臂的关节冗余度,使得机械臂在扩展任务(臂角+位置+姿态)特定的情况下,其关节空间有唯一解。需要指出的是,从物理意义上看,极端情况下,当机械臂快伸直时,臂角退化为一条直线,其无法有效表示机器人的构型,由此臂角是有一定范围的,否则容易出现奇异。
臂角也可以作为机器人避障碍的重要参数,机器人避障碍主要分为主动式避障碍和被动式避障碍;
- 在主动式避障碍的时候,臂角可以根据外部传感器(视觉、激光)来主动实现障碍回避。
- 在被动式障碍回避时,臂角调整根据关节力矩传感器的数值实现。
冗余机械臂的控制框架如下:
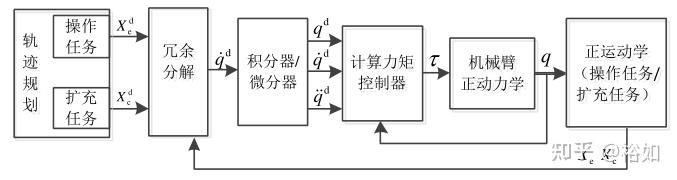
轨迹规划模块根据机械臂所需完成的任务进行相应的轨迹规划,例如对于冗余机械臂物体搬运任务,其主任务为将物体搬运至规定位置。
冗余机器人的位置控制核心是冗余分解模块。逆解的实际步骤包括:a设定关节极限,b计算雅可比矩阵,c奇异判断,d寻找最优解。利用运动学目标函数参数化冗余机械臂的自运动,是将笛卡尔空间轨迹直接通过雅克比矩阵转化为关节空间轨迹的逆运动模块,进一步通过阻尼最小平方法中参数的选择完成冗余机械臂的关节限位、避障规划等寻找最优解的任务。
以构型控制为例说明:选择笛卡尔主任务xe=f(q), ˙xe=Jf(q)˙q, 扩展任务,xc=g(q) , ˙xc=Jg(q)˙q,则定义x=[xe,xc]T ,˙x=J(q)˙q ,具体表示如下所示。
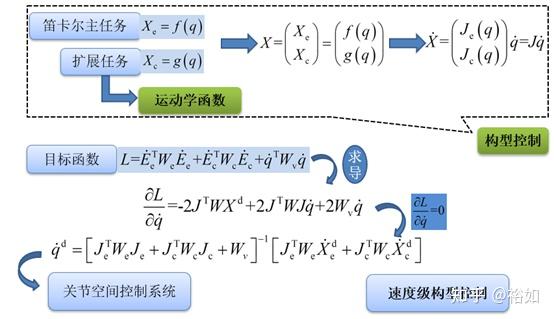
根据轨迹规划得到的运动学量不同,其可以分为跟踪目标位置的的位置控制、跟踪目标速度的位置控制或者为跟踪目标加速度的位置控制。本节采用基于跟踪目标速度的位置控制。对于基于速度级的冗余分解, 其生成的是关节角速度, 此时关节层控制器主要为了跟踪冗余分解生成的关节角速度。为了更好的跟踪期望轨迹,关节层控制器采用计算力矩控制。
搭建机械臂的全数值仿真系统
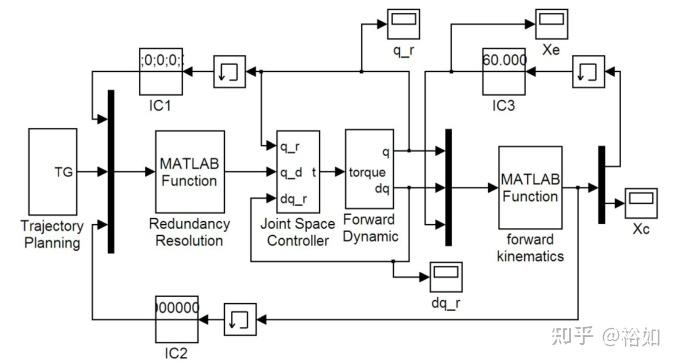
为了更精确的实现运动控制,该机械臂的运动控制系统为全闭环运动控制系统,其内闭环通过反馈关节角度进行关节空间位置修正,外闭环反馈笛卡尔轨迹进行笛卡尔空间位置修正,因而其位置控制精度较高。
参考文献:
[1] M. Shimizu, H. Kakuya, W. Yoon, K. Kitagaki and K. Kosuge, “Analytical Inverse Kinematic Computation for 7-DOF Redundant Manipulators With Joint Limits and Its Application to Redundancy Resolution,” in IEEE Transactions on Robotics, vol. 24, no. 5, pp. 1131-1142, Oct. 2008
[2] K. Kreutz-Delgado, M. Long, and H. Seraji, “Kinematic analysis of 7-DOF manipulators,” Int. J. Robot. Res., vol. 11, no. 5, pp. 469–481, 1992.





评论0