来源：https://zhuanlan.zhihu.com/p/1958983874689339600

机器人抓取与操作是具身智能领域最核心、最具挑战性的任务之一。它不仅仅是简单的“抓起来”，而是一个涵盖感知、规划、控制的复杂闭环系统。

一、核心挑战：为什么这么难？

在不确定的、动态的真实世界中实现可靠抓取，主要面临四大挑战：

1.感知不确定性

  • 物体多样性：形状、材质、纹理千变万化。
  • 遮挡：目标物体可能被其他物体部分或完全遮挡。
  • 光线变化：光照条件影响视觉传感器的精度。

2.物理交互复杂性

  • 动力学建模：抓取过程中的力/力矩控制、滑动、碰撞难以精确建模和预测。
  • 非刚性物体：处理衣物、电缆、食品等易变形物体是巨大挑战。

3.任务多样性

  • 从简单的拾取-放置，到复杂的工具使用（如用螺丝刀）、灵巧操作（如转动钥匙、叠衣服），对机器人的技能要求呈指数级增长。

4.Sim-to-Real（仿真到现实）鸿沟

  • 在仿真中训练的策略，由于模型不精确，在真实世界中的表现往往大打折扣。

如下图所示，即使简单的抓取日常物品，由于形状、重量、表面摩擦系数不同，导致最佳抓取方式等有非常大的差异。

二、关键技术模块解析

一个完整的抓取与操作系统通常包含以下模块：

1. 感知：看懂世界

  • 传感器：RGB-D相机（如Intel RealSense）、激光雷达（如Livox Mid-360）、触觉传感器。
  • 核心任务：
    • 物体识别与定位：目标在哪里？是什么？
    • 抓取位姿检测：直接回归出机械臂末端或夹爪的6D位姿。

2. 规划：决策如何抓

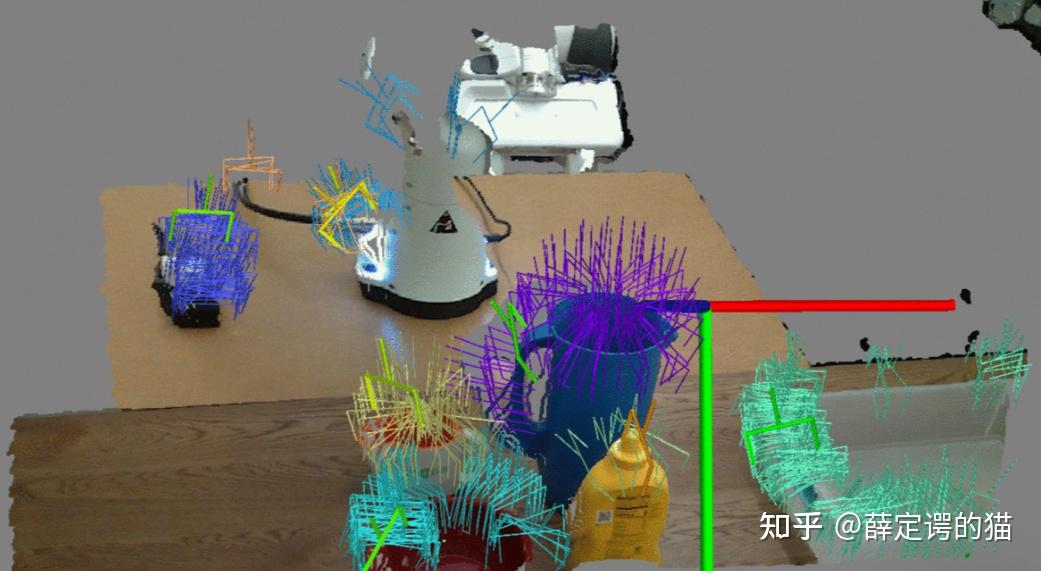
  • 抓取点检测：确定夹爪与物体的接触点。
  • 运动规划：规划一条无碰撞、平滑的轨迹，使机械臂从当前位置运动到抓取点。
  • 任务与运动规划：将高层任务（如“倒水”）分解为一系列meta action。
  • 传统规划方法

基于RRT算法为PiPER机械臂进行路径规划，是一个将经典路径规划算法应用于具体机器人平台的实践性课题。RRT算法核心思想：RRT通过快速扩展随机树来探索空间。它从一个起点开始，在空间中进行随机采样，然后将树向采样点的方向扩展一个固定步长，并通过碰撞检测确保路径安全。这个过程不断重复，直到树扩展到目标点附近。在ROS系统中可以通过MoveIt提供的API来设置规划场景（如添加障碍物）并请求路径规划，伪代码如下所示：

#include <moveit/move_group_interface/move_group_interface.h>

int main(int argc, char** argv)
{
  ros::init(argc, argv, "piper_rrt_planner");
  ros::NodeHandle node_handle;
  ros::AsyncSpinner spinner(1);
  spinner.start();

  static const std::string PLANNING_GROUP = "piper_arm";
  moveit::planning_interface::MoveGroupInterface move_group(PLANNING_GROUP);

  // 设置目标位姿 (例如，通过手势识别或其他方式得到的目标点)
  geometry_msgs::Pose target_pose;
  target_pose.position.x = 0.4;
  target_pose.position.y = 0.1;
  target_pose.position.z = 0.4;
  target_pose.orientation.w = 1.0;
  move_group.setPoseTarget(target_pose);

  // 规划并执行
  moveit::planning_interface::MoveGroupInterface::Plan my_plan;
  bool success = (move_group.plan(my_plan) == moveit::core::MoveItErrorCode::SUCCESS);
  if(success) {
    move_group.execute(my_plan);
  }
  return 0;
}
  • NN规划方法

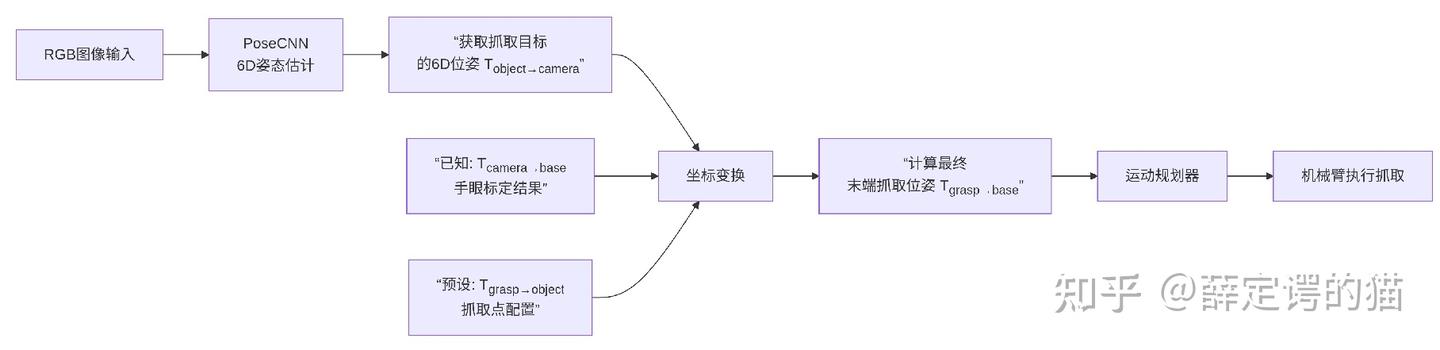
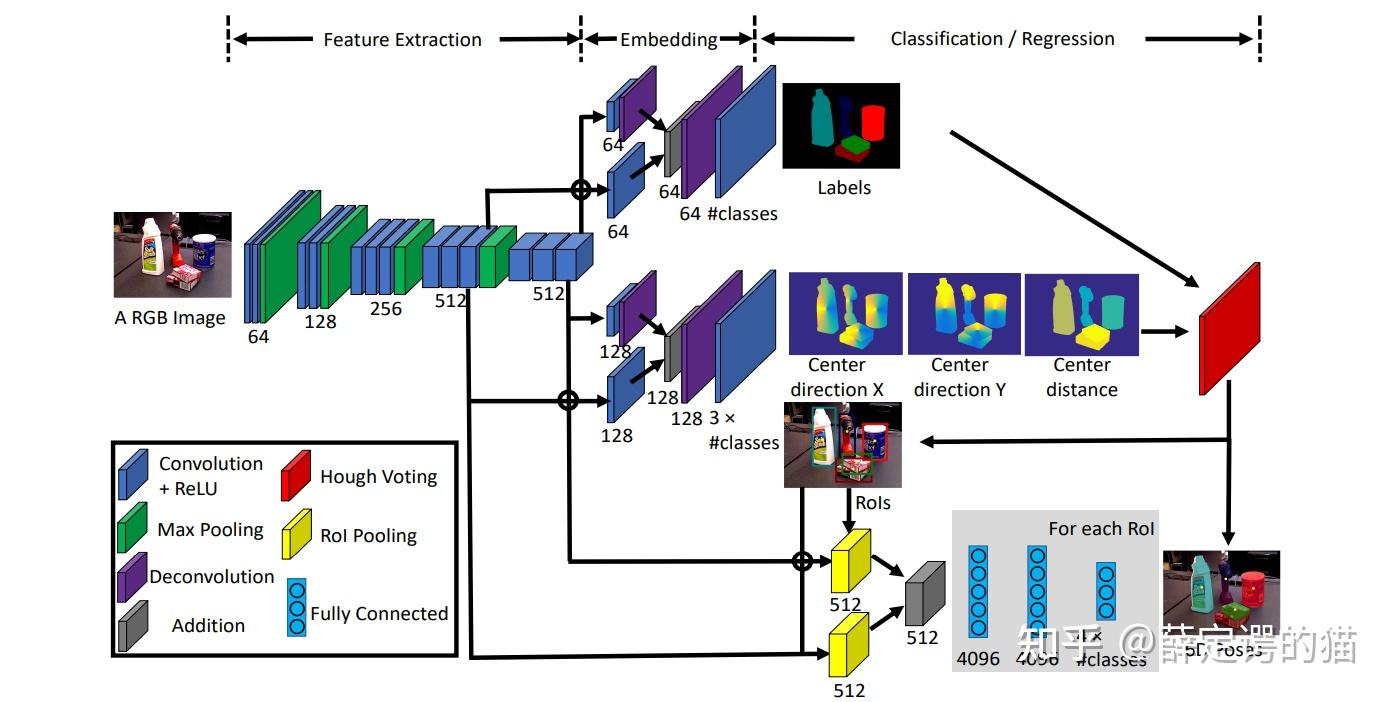
PoseCNN/GR-ConvNet/GraspNet是一个非常重要且经典的研究方向，提供了物体的6D姿态估计&抓取姿态，这为机器人实现精确、鲁棒的抓取提供了关键信息，然后再通过IK逆运动学解算可以得到机械臂各个关节的运动。

3. 控制：精准执行

  • 位置控制：控制机械臂到达指定位置。
  • 力控：在接触任务中至关重要，防止抓碎物体或损坏机器人。
    • 阻抗控制：让机器人表现得像是一个弹簧-阻尼系统。
    • 导纳控制：根据外力调整位置。
  • 抓取力控制：根据物体特性自适应调整夹爪力度。

力控制依赖力传感器来实时监测接触面上的力。传感器将检测到的力数据反馈给控制器，以便控制器根据设定的力目标来调整灵巧手的动作。在一些对外部扰动敏感的任务中，将位置控制和力控制结合起来，可以增强系统的稳定性。例如，在操作柔性物体时，加入力反馈可以帮助灵巧手在保持位置精度的同时避免施加过大压力。目前灵巧手还处于关节控制研究阶段，对于力控制还属于非常早期，不具备和人一样可以根据物体的受力特性进行抓取角度和力度调节。

三、前沿趋势与未来方向

当前，机器人抓取与操作正朝着更通用、更灵巧、更智能的方向发展。

1. 大模型赋能

大模型为抓取操作带来了语义理解和任务推理能力，是当前最火热的趋势。

  • VLA模型：如RT-2，能将自然语言指令（“把香蕉递给我”）直接映射为机器人动作，实现开放词汇的抓取。
  • LLM用于任务规划：让大语言模型（如GPT-4）充当“大脑”，将复杂指令分解为抓取操作序列。
    • 示例：指令“把桌子上的苹果和垃圾扔掉”，LLM可分解为：1. 找到并抓取苹果 -> 2. 移动到垃圾桶上方 -> 3. 释放苹果 -> 4. 找到并抓取垃圾 -> 5. 移动到垃圾桶上方 -> 6. 释放垃圾。

经典大模型可以参见《AI-Robot系列-VLA大模型》，虽然当下LLM/VLA概念炒得如火如荼，研究机构不断创新，但是实用性还是有限，个人觉得还是会先出现各种典型应用场景机器人，然后等机器人部署足够多可以收集更多数据后才会涌现出非常通用的VLA大模型。就像辅助驾驶一样，最开始也是简单L1/L2功能应用上车，等有足够的车辆采集返回数据后，才涌现出大量的端到端的算法，提升泛化能力和拟人能力，真实场景运行的机器人的数据是核心。

2. 仿真与Sim2Real

由于在真实机器人上收集数据成本高昂，在仿真中训练，再迁移到真实世界成为主流范式。

  • 高保真仿真器：NVIDIA Isaac Sim
  • 域随机化：在仿真中随机化纹理、光照、物理参数等，迫使策略学习更本质的特征，从而更好地适应真实世界。

目前已在四足机器人广泛使用，比如像奔跑、爬楼梯等无需和世界中的其他物体进行特殊任务交互的场景，但是在需要识别真实物体位姿并控制机械手操作等场景暂时还未做到很好的迁移性，不过已经可以生成细节逼真的场景，非常期待和真实物体交互的Sim2Real，或许可以真的大大减少对真实世界数据的依赖，加快具身智能的到来。

3. 灵巧手操作

从简单的二指夹爪发展到多指灵巧手，目标是实现像人手一样复杂的操作技能。

  • 挑战：高自由度（20+）带来的控制复杂度。
  • 方法：强化学习+模仿学习，在仿真中预训练。
  • 数据集：DexGraspNet等大规模灵巧抓取数据集推动了该领域发展。

4. 触觉感知

视觉告诉你“在哪抓”，触觉告诉你“怎么抓稳”。

  • 高分辨率触觉传感器（如DigiT）能提供丰富的接触力、滑动和纹理信息。
  • 应用：通过触觉反馈实时调整抓取力，防止物体滑落；识别物体材质。

四、逆向运动学

无论是基于传统方法还是NN方法，想要做到异构机器人通用是一个非常空难的事情，就好比辅助驾驶领域端到端，没有一个模型方案是直接输出控制结果（方向盘、油门、刹车），一般都会端到端输出驾驶轨迹，然后每个车型再根据实际的车辆控制特性进行底层控制，机器人更是如此，每个机器人的关节自由度形态差异非常大，通过端到端方法输出机械手末端的轨迹是一个比较可行的方案，那怎么分解到各个关节的运动控制呢，答案就是逆向运动学解算。

逆向运动学的两大核心方法：解析法和数值法。这两种方法代表了解决”从末端位姿求关节角度”这一经典问题的两种根本不同的哲学。

🧮 一、解析法

解析法，也称为闭式解法，是通过代数变换或几何关系直接推导出关节变量的数学表达式。

1. 核心思想

  • 利用机器人的几何结构和运动学方程，直接求解出关节角度的解析公式。
  • 对于每个目标位姿，将这些数值代入公式，即可直接计算出关节角度，无需迭代。

2. 三角几何学法详解

这是解析法的一种，特别适用于简单结构的机器人（如2自由度或3自由度的平面机械臂，或6自由度机器人的部分关节）。

  • 工作原理：
    将机器人的连杆结构视为一个几何三角形网络。通过已知的末端执行器位置 (x, y, z)，利用三角函数（如余弦定理、正弦定理） 和空间几何关系直接计算关节角度。
  • 经典示例：2R平面机械臂
    假设一个2自由度机械臂，两个连杆长度分别为 L1, L2。
    • 已知末端位置 (x, y)，求关节角度 (θ1, θ2)。
    • 求解过程：
  1. 计算到末端的直线距离： d = sqrt(x² + y²)
  2. 使用余弦定理求解 θ2：
    cos(θ2) = (x² + y² - L1² - L2²) / (2 * L1 * L2)
    θ2 = atan2(±sqrt(1 - cos²(θ2)), cos(θ2))（注意：这里通常有”肘部向上/向下”两种解）
  3. 使用正弦和余弦关系求解 θ1：
    θ1 = atan2(y, x) - atan2(L2 * sin(θ2), L1 + L2 * cos(θ2))

3. 优缺点

  • 优点：
    • 速度极快：计算是即时的，适用于高实时性控制。
    • 能获得所有可能解：可以系统地找出所有满足位姿的关节配置（如左/右臂、肘部上/下、腕部翻转等）。
    • 精确：不存在收敛误差，结果是数学上精确的。
  • 缺点：
    • 通用性差：严重依赖于机器人的具体构型。只有满足 Pieper准则（即机器人最后三个关节轴相交于一点）的6自由度机器人才有解析解。
    • 推导复杂：对于新的机器人模型，推导解析解需要深厚的数学和几何学知识。

🔢 二、数值法

数值法是一种迭代逼近的方法。它从一个初始猜测开始，通过一系列迭代计算，逐步缩小当前末端位姿与目标位姿之间的误差，直到满足精度要求。

1. 核心思想

  • 将逆向运动学问题转化为一个优化问题：寻找一组关节角度，使得末端执行器的当前位姿与目标位姿之间的误差最小。
  • 它不直接求解方程，而是通过迭代算法逐步逼近最优解。

2. 牛顿-拉夫森法详解

这是数值法中最经典和基础的一种。

  • 工作原理：
  1. 建立误差函数：定义末端位姿误差 e = f(θ) - x_d，其中 f(θ) 是正运动学函数，x_d 是目标位姿。
  2. 利用雅可比矩阵：雅可比矩阵 J 描述了关节速度与末端执行器速度之间的线性关系：ẋ = J(θ)θ̇。在迭代中，我们使用 Δx = J(θ)Δθ。
  3. 迭代求解：
  • Δx = x_d - f(θ_i) （计算当前误差）
  • Δθ = J⁻¹(θ_i) * Δx （计算关节角度的增量）
  • θ_{i+1} = θ_i + αΔθ （更新关节角度，α是步长因子，用于改善收敛性）

循环：重复步骤3，直到误差 ||Δx|| 小于预设阈值。关键点：

  • 雅可比矩阵的求逆：当机器人处于奇异位形时，J 是奇异的，无法求逆。此时通常使用伪逆J⁺ 或阻尼最小二乘法(JᵀJ + λI)⁻¹Jᵀ 来避免数值不稳定。

3. 优缺点

  • 优点：
    • 通用性强：适用于任何构型的机器人，包括冗余机械臂。
    • 易于实现：算法流程固定，对于任何机器人，只需实现其正运动学和雅可比矩阵计算即可。
    • 能处理约束：可以结合优化技术，在求解过程中加入关节限位、避障等约束。
  • 缺点：
    • 计算速度慢：需要多次迭代，计算量大于解析法。
    • 可能不收敛：依赖于初始值的选择，可能收敛到局部最优解或完全不收敛。
    • 只能得到一个解：每次运行通常只返回一个解，而不是全部可能解。
    • 存在奇异点问题：在奇异位形附近，数值行为不稳定。
赏 0

猜你喜欢

灵巧手常见的传动方案都有哪些？
学习

来源：https://www.zhihu.com/question/1960299903910650751/answer/196030378238...
1周前 33
机器人动力学库哪个更好？
学习

来源：https://www.zhihu.com/question/437857717/answer/1897953312235586570 ...
2周前 22
机器人灵巧手的关节怎么设计？
学习

来源：https://www.zhihu.com/question/27944838/answer/1953754270240335673 ...
3周前 37
马斯克说，人形机器人最难的不是大脑，而是灵巧手和量产。灵巧手为何那么难？
学习

来源：https://www.zhihu.com/question/1950897949698668255/answer/196256666940...
3周前 84
1350元入门具身智能-lerobot机械臂
学习

来源：https://zhuanlan.zhihu.com/p/1895609105902704289 前段时间一直在看具...
4周前 28
机械臂完成长程多步骤的组装任务
学习

来源：https://zhuanlan.zhihu.com/p/16403276747 FMB: a Functional Manipula...
4周前 34

评论0

取消

没有账号？注册  忘记密码？