机械臂是怎么运动的？（3）逆运动学、路径规划、轨迹规划、轨迹优化

来源：https://zhuanlan.zhihu.com/p/1897275522188293417

现在我们知道如何对操纵器进行建模，让我们回到实际的运动规划。系好安全带，深入了解逆运动学、路径规划和轨迹生成。在本节中，您将接触到成熟和最先进的算法，以及我个人对这些算法如何融入我们领域现有的运动规划工具包的见解。

1、逆运动学

我们在关节位置表达机器人手臂的目标是不自然的。我们通常更喜欢将机器人上的特定坐标系移动到目标位姿（位置和旋转）。例如，这可能是将机器人的手放在门把手上。这不仅适用于单一目标，也适用于需要遵循工具路径的任务，如焊接、擦拭桌子或倒杯子。在所有这些情况下，都需要逆运动学（IK）将任务空间中的笛卡尔目标转换为相应的关节位置。

在前面的部分中，我可能会吓到你认为IK是不可能的困难。虽然IK比FK更难，但有一部分问题可以通过分析来解决。如果你有能力做到这一点，你绝对应该这样做，因为它可以使结果保持一致，软件实现速度极快。这就是为什么几个工业臂具有恰好6个自由度，并且设计有球形腕关节机构，通过将IK解耦为使用3个腕关节求解旋转，使用另外3个求解位置，使数学更容易。虽然这个数学可以手工推导，但软件工具可以从机器人描述文件（如IKFast）自动生成分析IK代码。

在其他情况下，您可能需要依靠数值方法来求解IK。这并不总是坏事；虽然冗余机器人可能对给定的目标位姿有多个（甚至无限个）IK解决方案，但这种冗余可以帮助产生满足额外约束的解决方案，如避免碰撞或位置/方向边界。这就是为什么大多数协作机器人（cobot）手臂（如上图所示）都依赖于数值IK解算器。

根据我的经验，一种很少使用的简单数值方法是循环坐标下降法（CCD）。到目前为止，更常见的方法是逆雅可比矩阵或微分IK方法，我认为它在数学上更有原则，更具可扩展性。我们在这篇文章的前面介绍了几何雅可比矩阵，这里是它出现的一个地方。粗略地说，这种方法涉及循环中的以下计算：

• 计算当前位姿和所需位姿之间的位姿误差。（请注意，获取当前位姿需要正向运动学！）
• 如果误差在指定的公差范围内并满足任何其他约束，请返回解决方案。
• 使用逆雅可比矩阵*来获得朝向所需位姿的关节速度的一阶近似值。
• 朝那个速度方向迈出一步。

我们说将任务空间误差转换为关节速度需要反转雅可比矩阵，但我们确定在大多数情况下这是不可能的。因此，我们最终依赖于最小二乘回归中使用的Moore Penrose伪逆，或其阻尼最小二乘法（或Levenberg-Marquardt）来处理数值不稳定性。

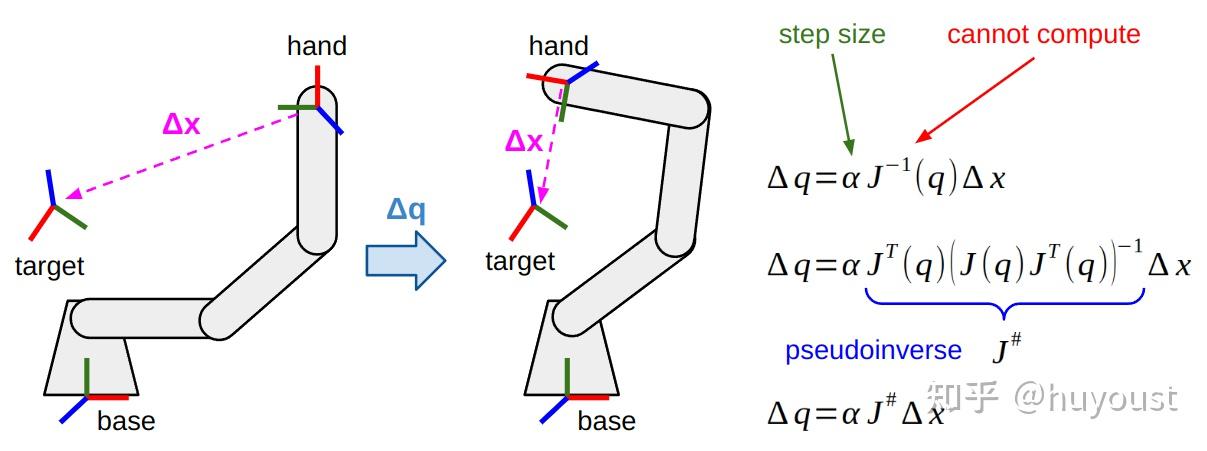
使用冗余操纵器，您可以使用这些基于雅可比矩阵的IK方法来求解主任务和一组辅助任务，只要它们不会干扰主任务。这可以通过“清零”次要任务中会干扰主要任务的所有组件来实现。从数学上讲，这是通过零空间投影完成的。你可以深入了解Samuel Buss论文中方程式（7）的数学原理，或者观看Leopoldo Armesto的这段精彩视频。

顺便说一句，这种方法有时被称为“任务堆栈”（SoT）；该领域的一位专家是Stéphane Caron，他不仅写了一篇关于IK的精彩博客文章，还实现了一个很酷的基于SoT的IK解算器Pink。Pink仓库中的示例展示了在使用人形机器人等高自由度系统时，堆叠任务可以走多远。另一个很好的例子是Fabrizio Flacco等人的零空间饱和（SNS）工作。

堆叠任务的一个例子是在避免碰撞的同时求解IK。如果你有一个冗余操纵器，也许你可以通过“肘部向上”或“肘部向下”配置来实现你的IK目标。然而，在这种情况下，“肘向上”解决方案可能会发生冲突。通过添加碰撞避免任务并将其投影到IK任务的空白空间，您可以将解决方案引导到“向下弯曲”解决方案。这也可以扩展到远离关节限制或朝向关节特定位置的约束，或保持任务空间中的位置或方向约束。

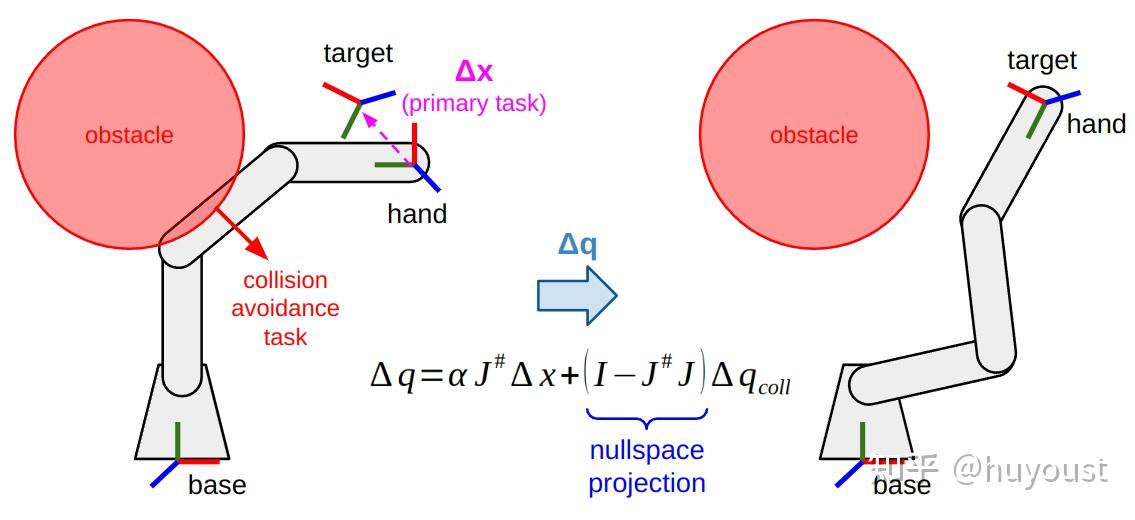
解决IK的另一种方法是非线性优化，许多最先进的IK解算器都应用了这种方法。一些例子包括：

• 零空间饱和（SNS）方法，该方法在基本算法中使用具有零空间投影的逆雅可比方法，但随后在其“Opt-SNS”变体中使用二次规划（QP）。我强烈建议查看Flacco等人2015年的论文，了解这种方法是如何演变的。
• Drake的IK解算器套件，都设置了各种各样的非线性优化程序，因为这是Drake的关键优势。
• TRAC-IK，它与非线性优化求解器并行运行一个常规的逆雅可比IK求解器（准确地说是KDL求解器）。然后，它返回它得到的第一个解决方案，或者在给定的时间预算内（取决于用户）的“最佳”解决方案。

事实上，Drake和TRAC-IK都依赖于非线性优化求解器包，如NLOpt和SNOPT，它们支持序列二次规划（SQP），在高度非线性的机械手运动学和约束条件下执行这些优化。 最后，值得一提的是，基于所提供的初始条件，数值方法容易受到局部最小值的影响。虽然全局优化技术已被应用于IK，但这些方法有其自身的缺点，尚未普及。例如，BioIK使用遗传算法，它可以找到全局最小值，但计算效率也非常低。

一种重量更轻、效果惊人的替代方案是在求解器中添加“随机重启”，希望尝试不同的初始条件会增加成功的可能性。我可以亲自为此担保；在最近的一个项目中，我正在对IK解算器进行基准测试。没有重试，我得到了令人不满意的50%的成功率；通过多达5次随机重启，这一比率跃升至99%。事实上，许多IK解算器都使用时间预算来实现这一点——换句话说，继续尝试，直到得到解决方案或经过一些最长时间。像NVIDIA的cuRobo这样的框架通过使用硬件加速（在这种情况下是GPU）来并行化这些随机尝试，将这一点提升到了一个新的水平。

2、基于搜索和抽样的规划

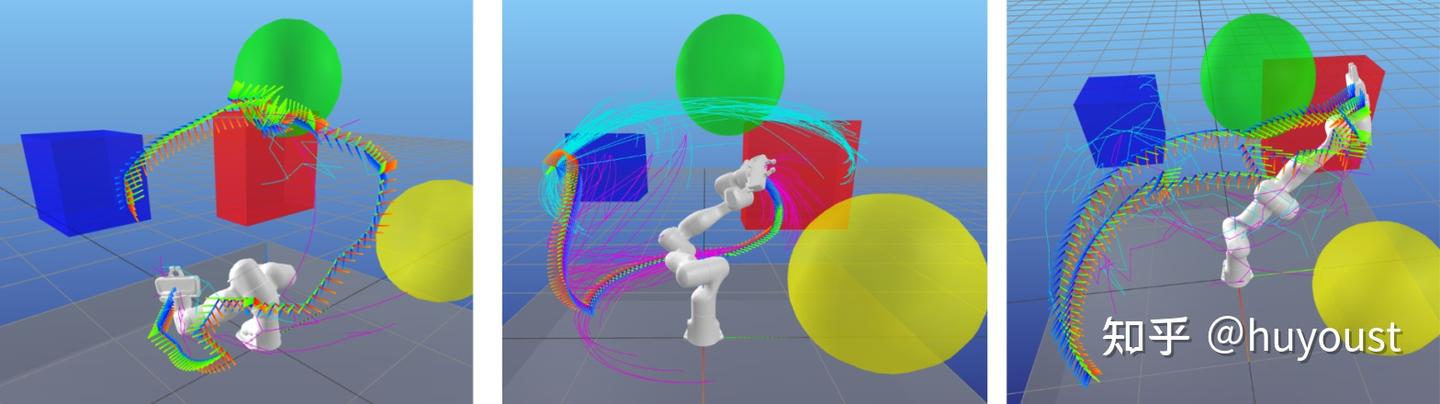
当使用能够向任何方向移动的2D移动机器人进行规划时，将世界离散化为网格并依靠您最喜欢的图形搜索算法来找到最佳路径相对容易。为了捕捉你的移动基地的一些复杂性，你可能会变得花哨，把你的机器人做成一个圆形、矩形，甚至多边形！当使用机器人操纵器进行规划时，这是类似的，除了我们现在在配置空间（即关节位置）而不是任务空间进行推理。像下面这样的图像，将现实世界的障碍物“扭曲”到机器人的配置空间中，通常用于介绍材料中，给人一种温暖的感觉，毕竟手臂并没有那么不同！您在右侧看到的路径位于配置空间中，然后转换回任务空间，根据机器人的几何形状，任务空间可能看起来完全不同。

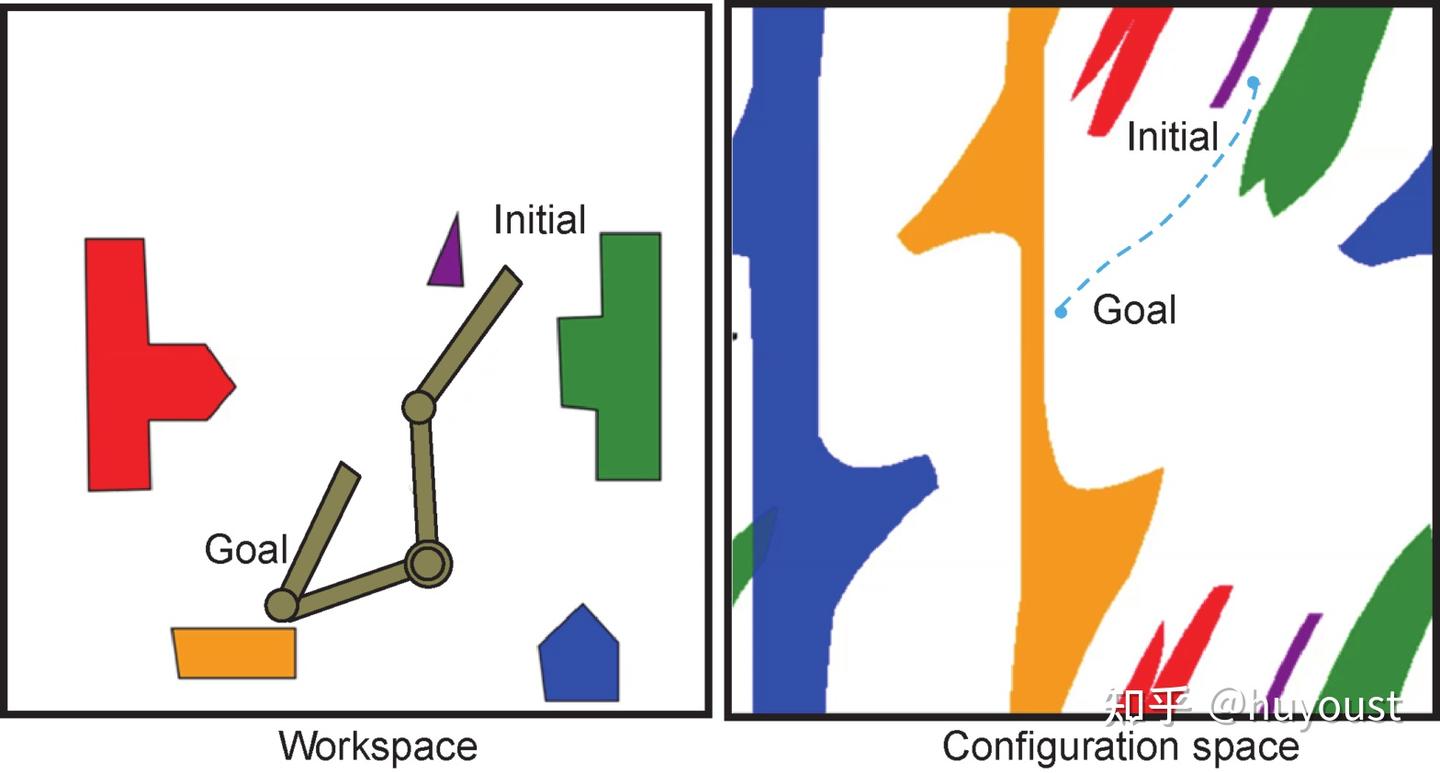
使用如上图所示的低维机器人手臂，您实际上可以使用广度优先搜索（BFS）、Dijkstra算法或A*（发音为A-star）等算法对配置空间进行离散化，并解决穷举搜索问题。

然而，对于高自由度机器人来说，这行不通。假设我们将每个自由度的关节位置划分为100个：我们的2自由度手臂将有一个多达10000个点的图形（如果我们有障碍物，则更少），这很容易搜索，而6自由度手臂最多有100^6个点

• 概率路线图（PRM）：这是一个多查询规划器，这意味着一旦你生成了一个随机采样点的图并将它们连接在一起，你就可以使用同一个图进行多次搜索。快速和可重用的运动规划需要大量的前期构建时间，这在静态环境中非常有用。
• 快速探索随机树（RRT）：这是一个单一的查询规划器，这意味着树（一种图）从一开始就“生长”到目标，然后被丢弃。顾名思义，RRT比构建整个PRM更快，但它们是一次性的。有时，RRT是双向的，这意味着两棵平行的树从起点和终点生长，它们在在中间的某个地方连接。

如果你想了解更多关于PRM和RRT的信息，一个很好的入门资源是Kris Hauser的《高维运动规划》一章。您还可以参考PRM和RRT的原始论文，了解一些不太遥远的历史。

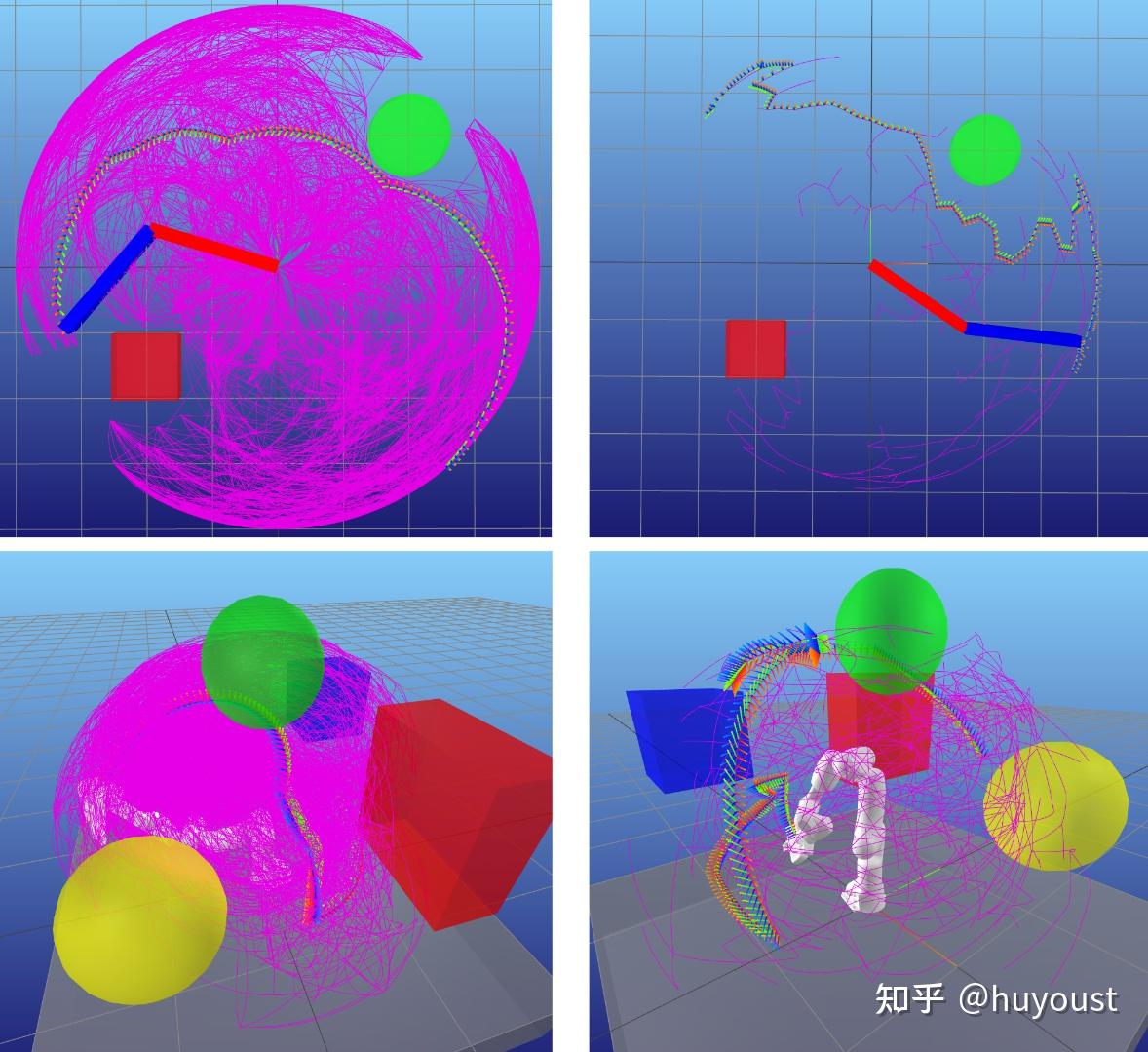
正如你所看到的，这些路径看起来……很奇怪。在机器人专家中，取笑基于抽样的规划者们的“RRT舞蹈”是一种常见的消遣。有一些方法可以缓解这种情况，但就像任何基于采样的方法一样，除非你有无限的样本，否则无法保证……所以，永远不会。一些常见的策略是：

• 算法变体：这些变体包括RRT*和PRM*（分别发音为RRT-star和PRM-star），它们试图在运行中重新布线图形，从而牺牲一些速度来提高路径质量。Sertac Karaman和Emilio Frazzoli在2011年的论文中介绍了这两种方法。如果你去维基百科上关于RRT的页面，并前往“变体和改进”部分，你会发现一个压倒性的额外调整列表。请放心阅读，风险自负。
• 捷径：尝试采用现有的“古怪”路径并沿其采样点……你猜对了……在这些点之间找到捷径。一些了解更多关于快捷方式的好资源包括Kris Hauser书中的这一部分，以及Valentin Hartmann的这篇博客文章。
• 优化：我将把细节保存在优化部分，但你可以使用非线性优化技术来优化来自基于采样的规划器的路径。

我们还应该谈谈碰撞。运动规划要求从起点到终点的整个路径无碰撞。操纵器等系统带来的另一个复杂性是碰撞检查也变得更加具有挑战性。例如，对于移动机器人，我们通常可以将机器人表示为圆形或简单的多边形（或其3D等效物）。如果机器人和障碍物的几何形状都是凸形的，则可以保证两个无碰撞配置之间的直线段也是无碰撞的。对于操纵器，验证路径段的一种方法是在配置空间中离散这些直线路径，并在每个样本上执行碰撞检查。这不仅在计算上很昂贵（特别是如果你的碰撞几何体是全网格），而且如果你的采样分辨率太粗糙，或者你在拐角处遇到障碍物，你的规划器可能会误将路径标记为无碰撞！在其他情况下，您可以计算沿直线移动的此类几何体的扫掠体积，并执行一次碰撞检查。

最后，值得强调的是，这些规划者的基本实现纯粹是运动学的。也就是说，它们将产生无碰撞的路径，但我们仍然需要弄清楚如何将这些路径转换为机器人可以执行的轨迹，包括尖角和蜿蜒的路径。有一大群运动学规划者，他们在机器人能做的运动学/动力学极限内对可行的运动进行采样，但在实践中，这些往往只适用于自主移动机器人、类车机器人或无人机等简单系统。事实上，像混合A*或动力学RRT这样的规划者在这些环境中得到了广泛的应用，但在更大的动作空间和高自由度的组合使其难以应用的操作中，你看不到它们的身影。

3、轨迹生成

一条路告诉你去哪里，但不告诉你什么时候去。传统上，轨迹生成是对一系列航路点指定的路径进行“计时”的过程。无论这是直线关节路径还是防撞RRT的多路点路径，都适用相同的原则。轨迹生成有多种方法，每种方法都有其独特的优缺点。

由于物理定律，我们遗憾地不能让一个真正的机器人以恒定速度直线移动，随意启动、停止和改变方向。我们当然可以命令执行器尝试遵循这些美化的阶跃响应，但这是一个经过验证的缩短执行器寿命的方法，而且可能不会获得太好的路径跟踪性能。

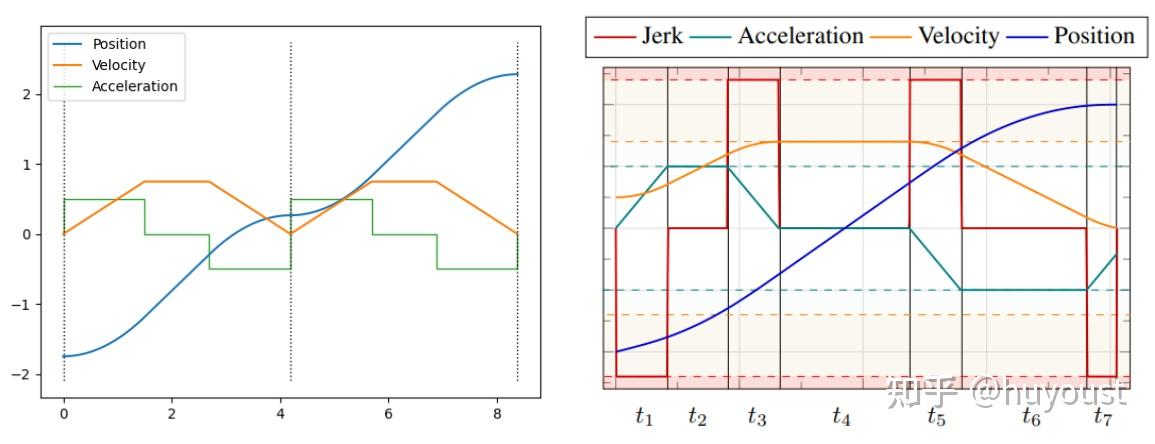
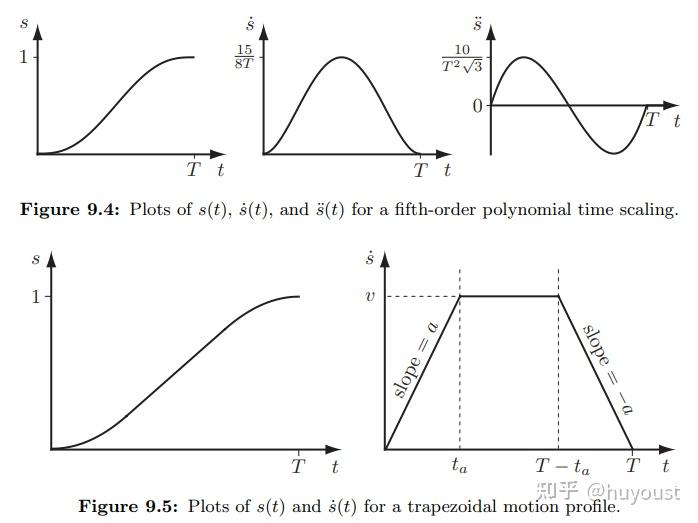
工业臂通常依赖于梯形速度剖面，也称为抛物线混合线性段（LSPB）。这些轨迹易于参数化，并保证遵守运动学限制，因为航路点永远不会超调；所有分段都以零速度开始和结束。但是，如果你看下图左侧的轮廓，你会发现加速度在路径段之间不连续地“跳跃”。我们可以通过将轨迹表示扩展为梯形加速度分布来解决这个问题，更常见的是s曲线（如右图所示）。Ruckig库是s曲线轨迹生成最著名的实现。

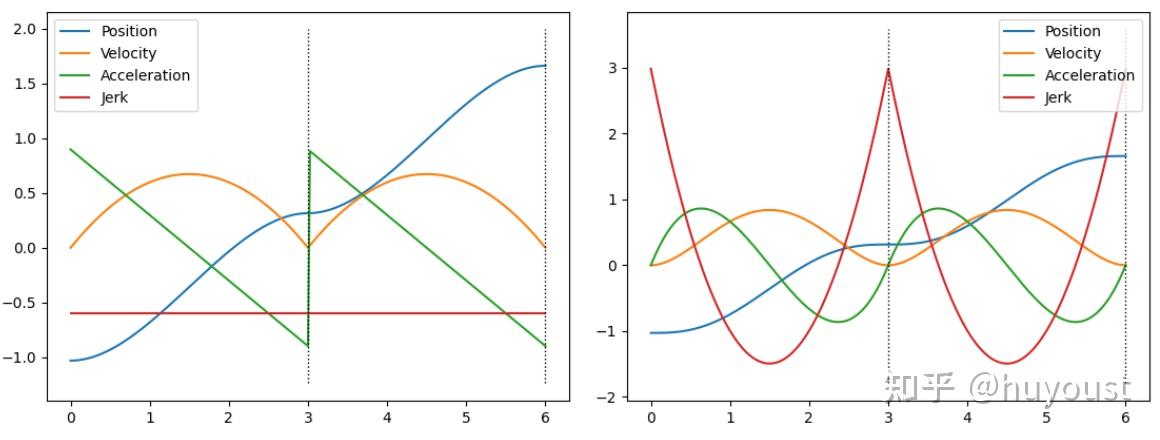
其他常见的轨迹生成方法涉及多项式。多项式具有显著的优势，因为它们易于拟合、可微，并且连续到它们的阶（或度）。如下图所示，多项式轨迹最常见的实现方式是三次（三阶）或五次（五阶）。你有时会听到“最小急动”和“最小快动”轨迹，它们是多项式轨迹的具体体现，可以最小化位置的导数。这段来自宾夕法尼亚大学在线课程的视频很好地解释了基础知识。

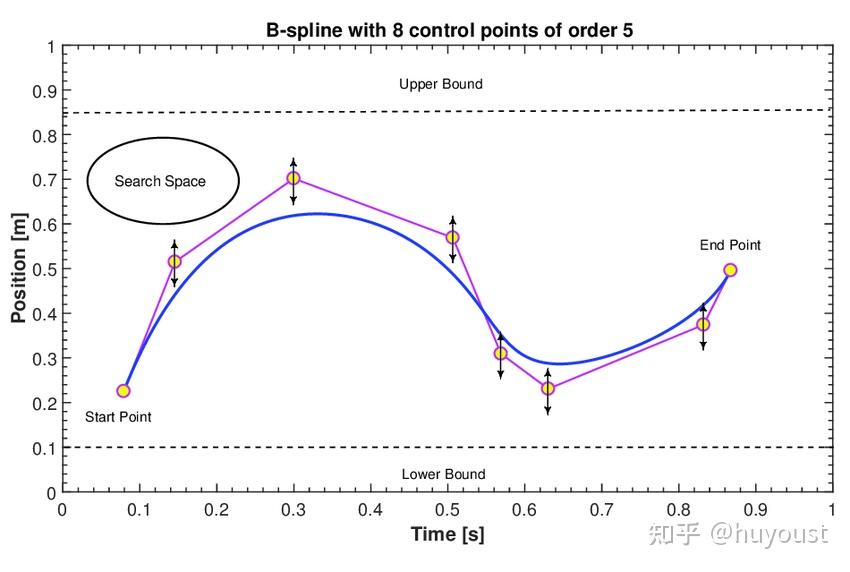
由于多项式轨迹与梯形速度轨迹没有相同的约束，即使边界条件都安全地在关节限制范围内，也不能保证中间点。存在其他基于多项式的表示来解决这个问题，例如B样条或贝塞尔曲线。样条线通常也能保证平滑的导数，但它们也由控制点定义，控制点保证所有中间点都在点的凸包内（见下图）。虽然这是以轨迹更保守为代价的，因为它们不能“超过”凸包，但这可能是一个很好的权衡，以确保安全。

其他流行的方法依赖于数值积分来计算满足速度和加速度限制的轨迹。最常见的是时间最优轨迹生成（TOTG），它试图在最大加速和减速段之间交替，同时保持在运动学极限内。这是一个很棒的TOTG解说视频。

一种相关的方法是基于可达性分析的时间最优路径参数化（TOPP-RA）。这在从最终速度计算可到达集合的向后通过轨迹段之间交替，然后是从可控集合中选取输入的向前通过，使得每个段都在下一个段的可到达集合中结束。TOPP-RA通过求解一组线性程序来生成类似的轨迹，而不是计算成本高昂的数值积分。

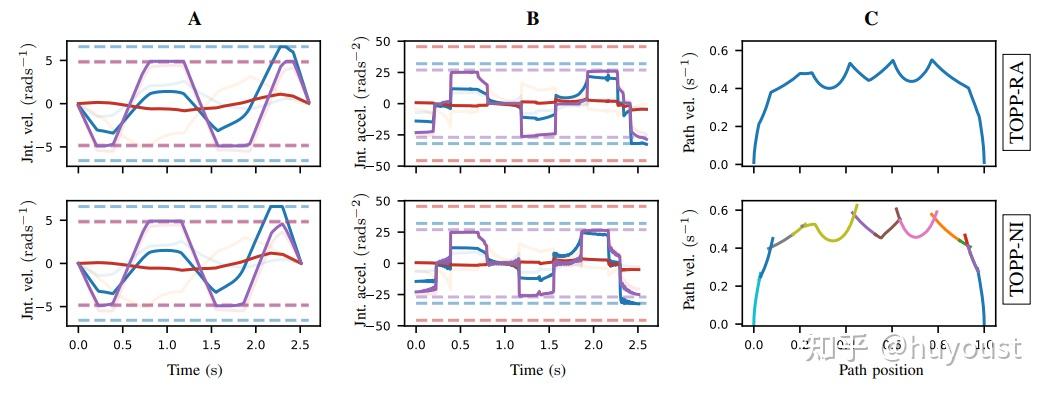
如需深入了解本节内容，请查阅《现代机器人》一书的第9章。然而，我们稍后将讨论基于优化的轨迹生成方法。不过，让我们先稍微绕道而行。

4、笛卡尔空间规划

我们花了一些时间哀叹机械手运动学和动力学是非线性的。这意味着配置空间中的直线在现实世界（或任务空间）中不是直线。因此，例如，如果你需要你的机器人在现实世界中遵循规定的刀具路径，就需要一种稍微不同的方法。

从数学上讲，我们在上一节中介绍的轨迹生成方法也可以表示为直线路径上的时间缩放。

虽然到目前为止我们看到的所有轨迹都在关节空间中，但没有什么能阻止我们在笛卡尔空间中做同样的事情。在笛卡尔轨迹中，有6个自由度（3个平移+3个旋转）。然而，由于旋转，“直线路径”的定义有点复杂。定义这样一个细分市场有两种选择。

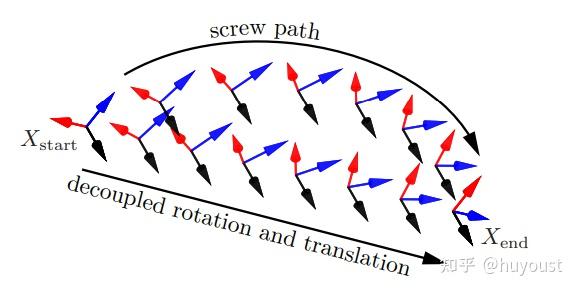
• Constant screw motion：这将旋转和平移结合起来，使从开始到结束都有持续的扭曲。你可以把这看作是围绕空间中的一个固定点沿着“弧线”移动。这种方法在打开或关闭门等任务中很好，在这些任务中，螺钉运动可以围绕现实世界中的实际铰链进行定义。
• Decoupled rotation and translation：这涉及平移和旋转自由度的单独线性插值。如下图所示，这使得翻译组件在任务空间中成为一条实际的直线。因此，这种方法适用于需要忠实地遵循任务空间中的路径的任务，包括绘图、涂漆或焊接。

笛卡尔插值通常是通过使用李代数来表示变换来完成的（您可以在本教程中了解更多信息）。旋转分量的另一种常见方法是球面线性插值（Slerp），这是我们在计算机图形学界的好朋友开发的一种插值四元数的方法。

综合起来，你可以采用直线笛卡尔路径，并对它们应用你最喜欢的时间缩放（梯形速度、多项式等）。与关节空间轨迹一样，您可以同样地提出将生成的轨迹保持在指定的笛卡尔空间速度、加速度和急动度限制内的定时。我最喜欢的笛卡尔轨迹资源是Alessandro de Luca的这些幻灯片，因为它们也谈到了在拐角处混合，以避免在中间航路点停车。

最后一件事仍然存在：将笛卡尔轨迹的每一步转换为控制器的实际关节角度。这意味着逆运动学！幸运的是，在这些情况下，IK问题可以逐步解决，因为一个轨迹点的解决方案对下一个点来说是一个很好的初始猜测。

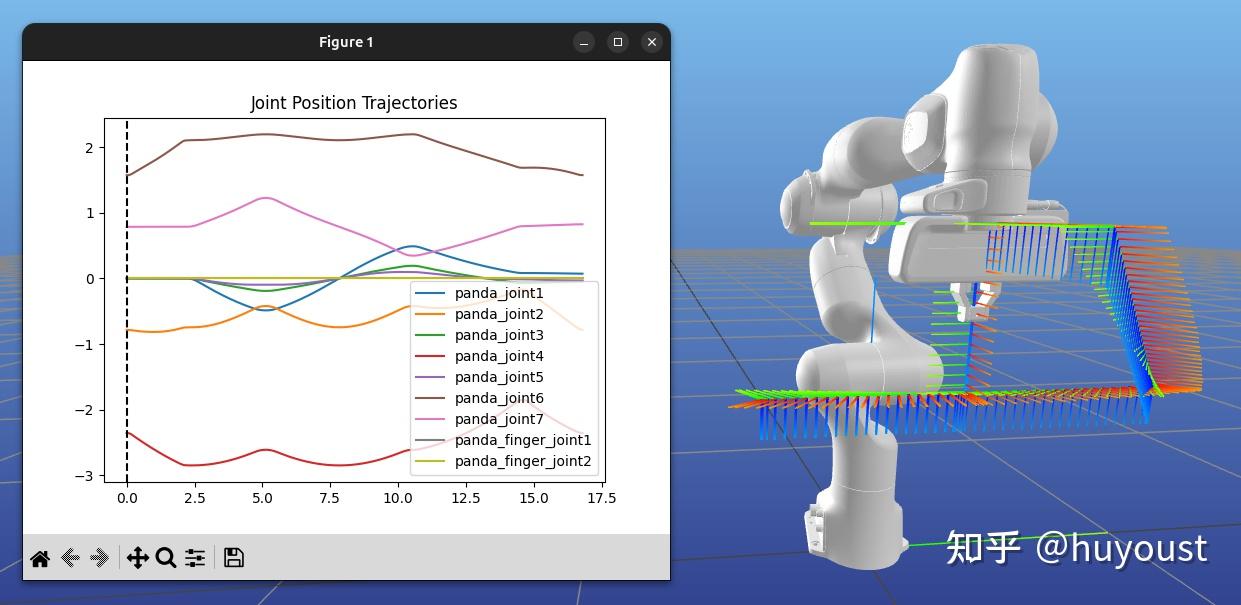
不过，还有一些事情需要考虑：

• 虽然可以生成笛卡尔轨迹以保持在笛卡尔运动学限制内，但这并不能说明IK步骤后关节限制的满足程度。因此，您可能需要进行另一轮验证（甚至重新命名）。在实践中，我们经常选择保守的笛卡尔极限，以最大限度地提高满足联合极限的机会。
• 在沿整个轨迹求解IK时，您仍然可能陷入局部最小值，无法生成完整的解决方案。冗余操纵器当然有助于缓解这种情况，但有时您可能需要依赖其他技术，例如尝试不同的IK解决方案，或放宽沿某些自由度对笛卡尔轨迹的精确遵守（例如，平移可能比方向更重要）。

在笛卡尔约束还需要与其他约束（如碰撞避免）竞争的环境中，上述这些预定义的直线路径可能还不够。例如，想象一下，在不碰撞的情况下，将一杯水举过墙壁。存在一些试图向自由空间运动规划器添加笛卡尔约束的方法。例如，Berenson等人2009年的这篇论文增强了RRT，使其能够将采样点投影到约束流形上，例如笛卡尔平移和方向限制上的边界体积。

5、轨迹优化

处理我们讨论过的许多运动规划问题的另一种方法是优化。通常，优化问题由一个最小化的成本函数和一组约束组成。对于大多数机器人应用，这些需要是非线性优化问题，因为机器人的运动学和/或动力学以及复杂的约束（如碰撞避免）通常是非线性函数。

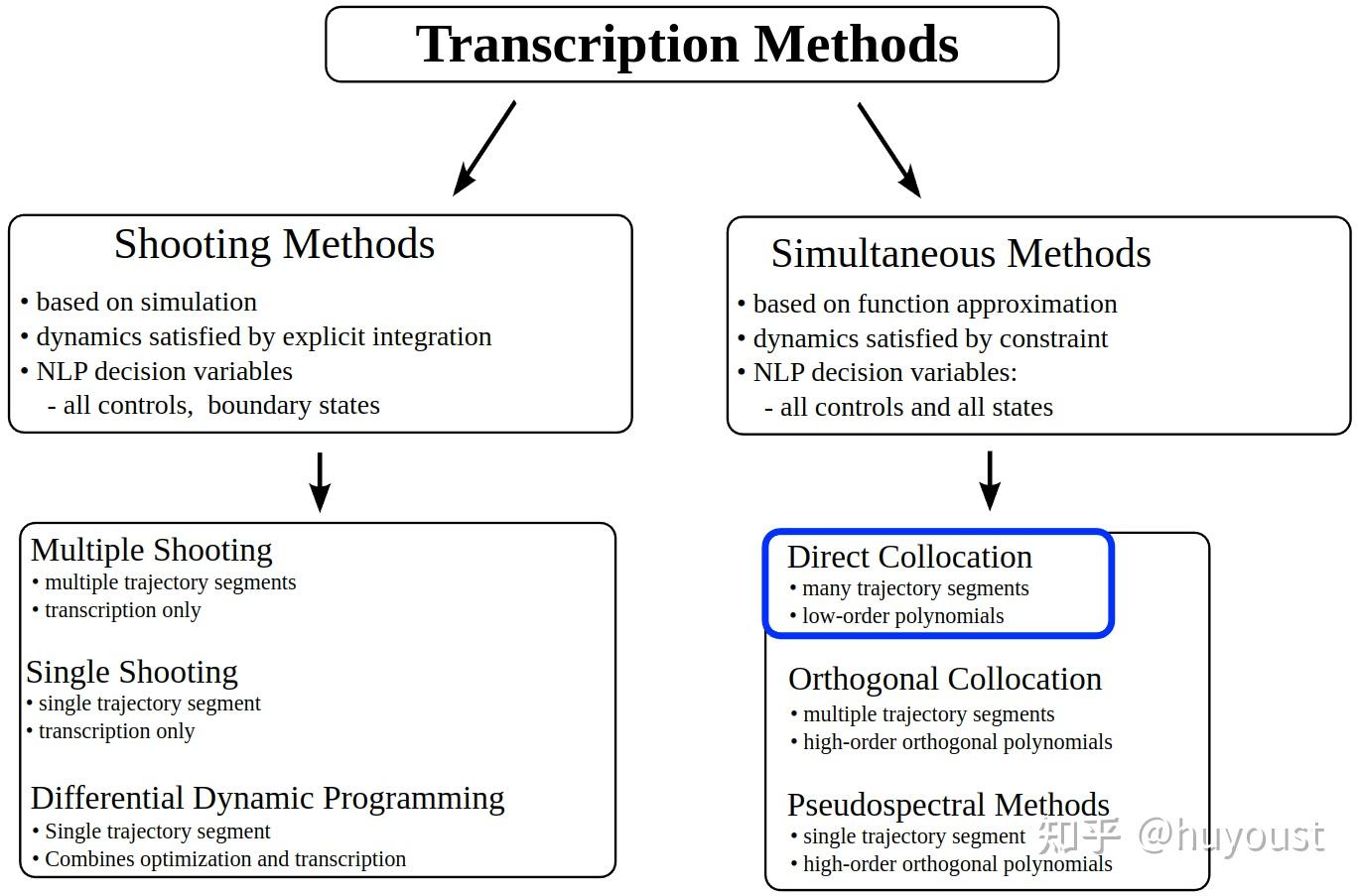
将轨迹转换为优化问题的任务称为转录（如，将轨迹转录为非线性程序）。您将遇到的两种主要方法是：

• Direct transcription：这涉及将轨迹离散化为时间样本。这些样本通过必须服从机器人的运动学和/或动力学而相互约束。虽然你可以通过这种方式直接优化关节（或笛卡尔）位置，但这种方法的一个常见子类是只优化控制输入（力/扭矩等），让机器人动力学决定位置如何随时间变化。这些被称为射击方法，指的是射击大炮并让动态随着时间的推移而展开。
• Direct collocation：正如你所想的那样，对长轨迹进行精细离散意味着你可能需要优化大量的关节（或笛卡尔）点。事实上，即使我们应用射击方法来减少变量的数量，这也可能效率低下。相反，搭配方法在轨迹上强加了一个数学结构；例如多项式段。这使我们能够在数量少得多的决策变量上解决优化问题，例如分段的边界条件或多项式系数本身。

在实践中，直接转录方法更常用于短期控制，而搭配方法则用于将完整路径转换为轨迹。

关于轨迹优化的最佳资源之一是Matthew Kelly的这套教程，他目前在波士顿动力公司研究Atlas人形机器人。Russ Tedrake的欠驱动机器人课程也有一个关于轨迹优化的精彩章节。

一些常见的基于转录的实现在机器人技术中取得了成功，包括：

1. Ratliff等人（2009）的运动规划协方差哈密顿优化（CHOMP）。使用梯度下降来优化轨迹中的点，同时满足碰撞避免等约束。
2. 运动规划的随机轨迹优化（STOMP）（Kalakrishnan等人，2011）和运动规划的增量轨迹优化（ITOMP）（Park等人，2012）。这些是无梯度方法，依赖于生成有噪声的轨迹——因此是随机的——在满足约束的同时进行类似的优化。
3. Schulman等人（2013）的TrajOpt框架使用序列二次规划（SQP）进行轨迹优化。在我看来，这让我们进入了我在撰写本文时所认为的“现代”方法。TrajOpt已被多个软件包采用，其中最著名的是Tesseract作为ROS Industrial计划的一部分。有关更多信息，请参阅这篇文章。

对于直接搭配的方法，德雷克可能是最著名的产品。Drake提供了DirectCollocation和KinematicTrajectionOptimization类，分别使用三次样条和B样条参数化执行直接配点。在Drake中，您可以向数学程序添加任意约束，这意味着您可以用自己的运动学/动力学限制、位置/方向限制、碰撞避免等约束来增强上述问题。

无论你选择哪种优化方法，一种简单有效的方法是使用最简单的“路径规划器”作为初始猜测。也就是说，假设一条直线路径有均匀间隔的路点，让优化器挤掉所有可能违反的约束。

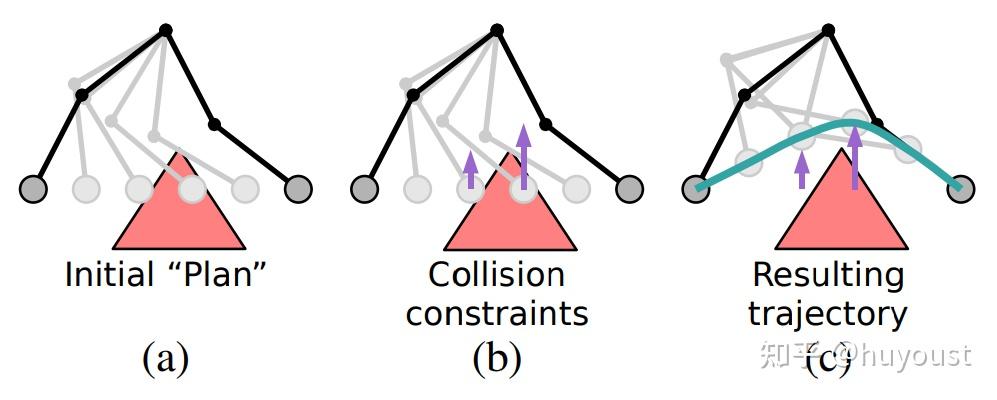
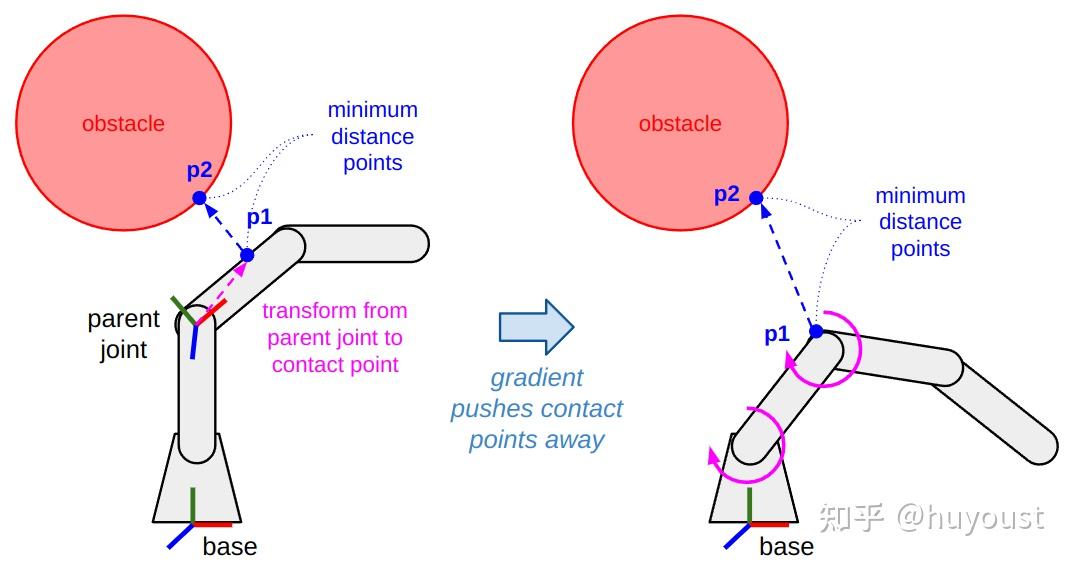
1. 在IK或轨迹优化中添加碰撞避免约束是我花了很长时间才弄清楚的事情。因此，我想在这里详细说明一下，以防你同样感到困惑。以下图为指导，总体思路是：
   
   找到一个表示碰撞（或接近碰撞）的向量。如果你有简单的形状，比如球体或胶囊，你可以通过分析找到它。否则，你可以依靠你最喜欢的碰撞检查库来给你一对分数。
2. 找到接触点的父关节。例如，在我们的图中，手臂上的接触点（p1）是第二个关节的父节点。也就是说，父关节和p1之间的变换是不依赖于任何关节位置的刚性变换。
3. 计算两个接触点处的雅可比矩阵。这是通过在父关节处变换雅可比矩阵，并在关节和接触点之间进行额外的刚性变换来实现的。这被称为接触雅可比矩阵。
4. 定义梯度。在我们的例子中，梯度将使用接触雅可比矩阵在与碰撞距离矢量相反的方向上移动前两个关节。如果p1和p2都恰好在机器人的运动部件上（所以这是一个自碰撞检查），你可以使用两个单独的接触雅可比矩阵将这两个点推离彼此！

有了这些信息，如果你想了解真正的数学细节，请查看TrajOpt论文的第四节（Schulman等人，2013）和Chiu等人，2016年的论文的第三节。

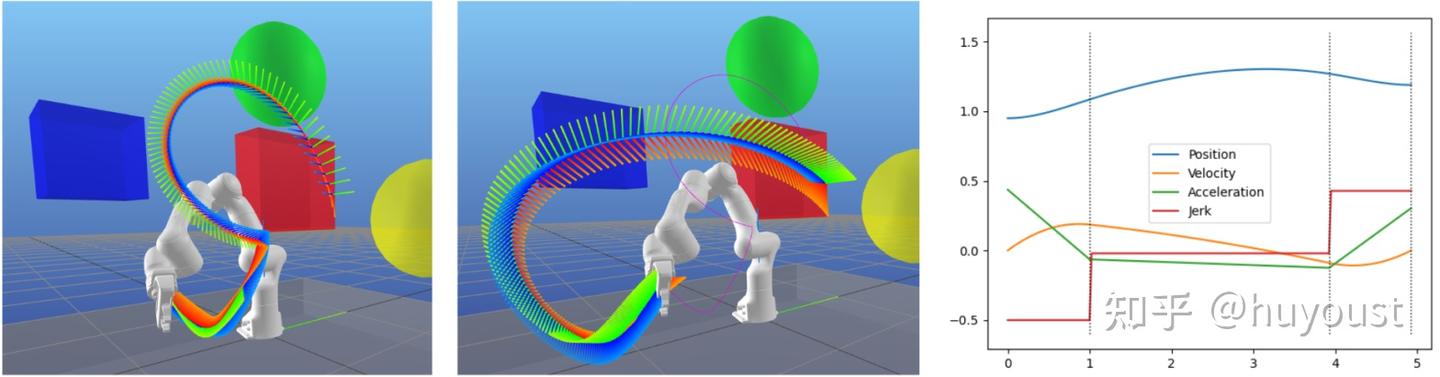
不幸的是，非线性优化对初始条件也非常敏感。虽然直线路径作为初始种子可能是有效的，但它会在充满障碍的复杂环境中崩溃。一种常见的补救措施是使用真正的路径规划器。例如，您可以使用RRT生成次优路径，然后通过优化对其进行改进。

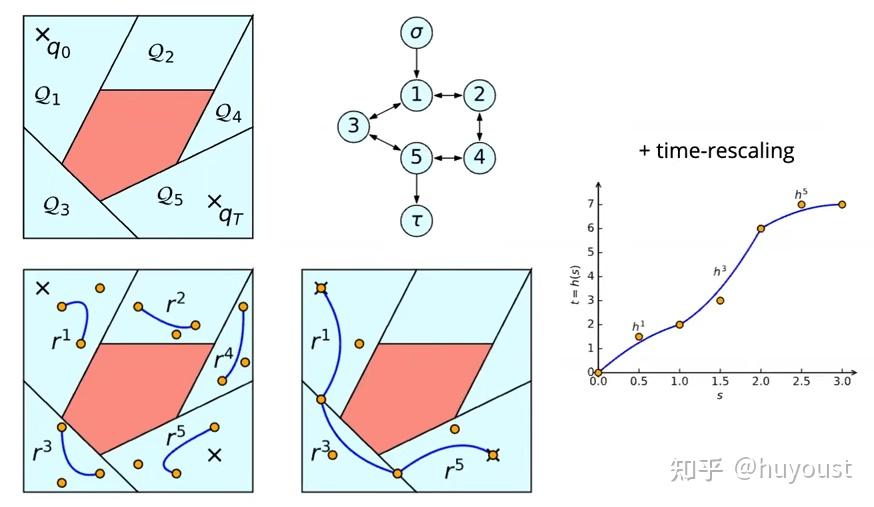
其他最先进的方法试图将搜索和优化结合起来。其中最有前景的是Russ Tedrake团队于2021年首次推出的凸集图（GCS）。GCS首先执行（计算上昂贵的）预处理步骤，将环境分解为凸分量。然后，它应用图搜索来找到从起点到目标组件的凸集图的路径。在每个组件中，您可以执行优化以获得物理上一致的轨迹。由于图分量是凸的，并且它们选择了B样条作为直接配点方法，因此可以保证每个轨迹段都保持在凸集内！酷，对吧