来源:https://zhuanlan.zhihu.com/p/15964694881
0、前言
初学机器人,运动学建模是前期必须熟练掌握的基础,运动学分析说到底其实就是空间几何坐标的变换,因为这里面用的是刚体假设,不考虑实际连杆的受力与变形。本文的内容主要来自教科书,只不过做了一点整理,力求逻辑连贯,方便理解。同时以UR3e机械臂为例进行辅助说明。
该系列文章分为三篇:上篇介绍DH参数法,中篇介绍POE参数法,下篇介绍《仿人机器人》一书中的参数法(不知道具体叫啥方法)。
文中提到的教科书的电子版可以参考另一个文章:
huyoust:机器人领域相关经典教材30 赞同 · 2 评论 文章
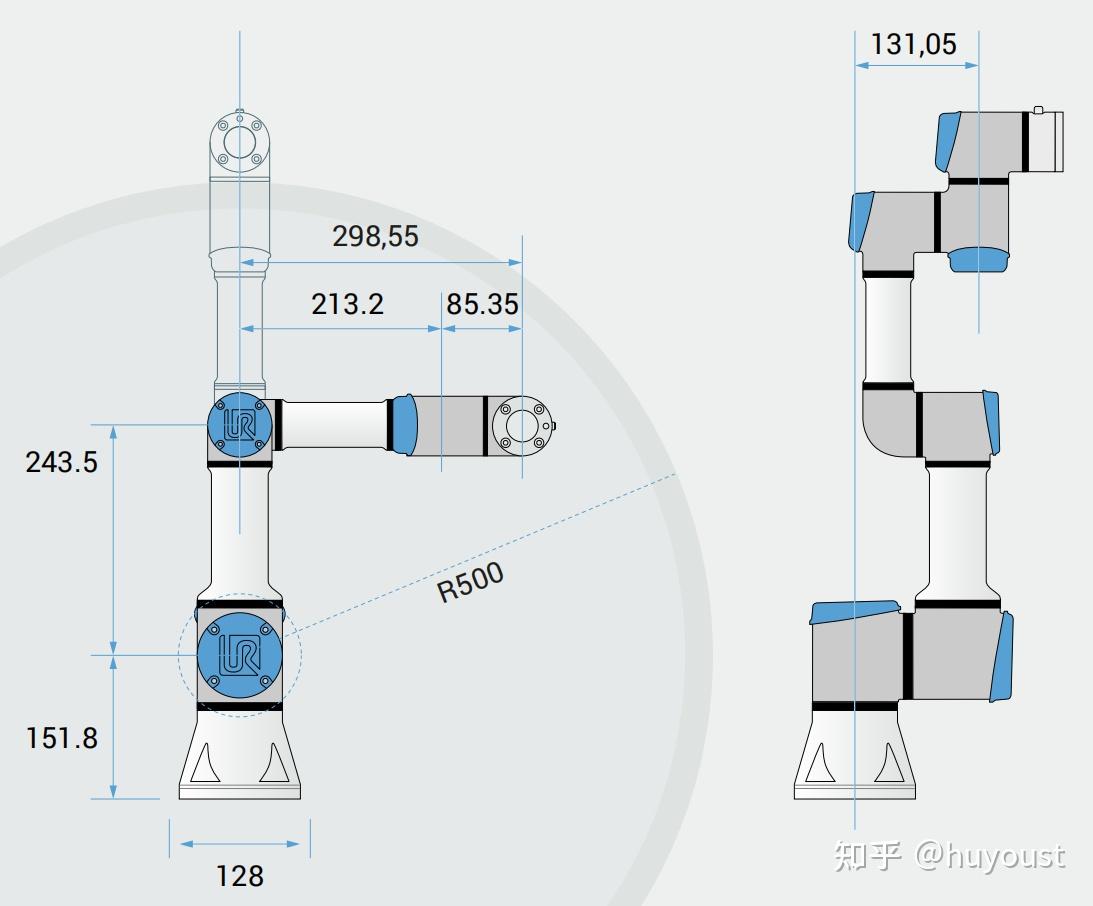
此处还是以UR3e机械臂作为例子介绍,关于UR3e机械臂的相关资料可以参考官网,其主要尺寸如下:
1、DH参数法相关的坐标变换基础
1.1、相对位姿与齐次矩阵
连续变换的叠加是理解各种运动学建模方法的基础,也是机器人运动学建模的底层逻辑,无论是DH参数法,还是矢量积法,底层的逻辑都是连续变换的叠加。在此之前,先了解一下齐次矩阵。齐次矩阵其实是为了数学描述上统一的方便,根据矩阵运算的规则,将旋转与平移放在一起用矩阵描述。

如上图所示,考虑两个坐标系 {�} 与 {�} ,同一个点/向量P在坐标系 {�} 与 {�}下的描述分别为 �� 与 �� 。它们之间的关系可以描述为:��=�����+������其中 ������ 为坐标系 {�} 的原点在坐标系 {�} 中的位置, ��� 为坐标系 {�} 相对于坐标系 {�} 的姿态。上式中既有矩阵乘法又有向量加法,对于追求简洁的数学来说,不够美观。为了让上式看起来就跟原点相同的不同坐标系之间的变换公式 ��=����� 一样简洁,将上式改写为[��1]=[���������0001][��1]这样将 [���������0001] 定义为一个新的矩阵 ��� ,那么 ��=�����+������ 就可以写为:��=�����这样的矩阵 � 叫齐次变换矩阵(这种矩阵 � 的集合通常叫做 ��(3) 群)。根据几何解释, ��� 既可以理解为同一个点在不同坐标系下变换的算子,也可以理解为这两个坐标系之间的相对位姿,还可以理解为描述了一个相对某个世界坐标系的坐标系的姿态。
1.2、多个坐标系之间的位姿传递
假设有 �+1 个坐标系,编号分别 {0} 到 {�} ,相邻编号的坐标系之间的变换矩阵(或者说相对位姿)为 ��−1� 。根据前面的介绍,同一个点在坐标系 {�} 下的位置为 �� ,那么自然有:0�=10�21�⋯��−1���以及:0�=�0���所以两边对比一下就有:�0�=10�21�⋯��−1�这就是连续变换的链式法则,也即位姿之间的传递,这个公式看起来简单,却是理解机器人运动学相关计算的基础。有了这几个公式基础,就可以分析机械臂的运动学了。机械臂正运动学问题解决的是计算末端工具相对于机械臂基座的位姿。
1.3、绕固定坐标系与运动坐标系的左乘与右乘
相关内容可以参考另一篇:
huyoust:机器人理论基础:相似变换与连续旋转的左乘/右乘91 赞同 · 11 评论 文章
这里补充几点关于术语的解释
左乘:也叫前乘,对应pre-multiply、pre-multiplication;
右乘:也叫后乘,对应post-multiply、post-multiplication;
�� : � is post-multiplied by � ; � is pre-multiplied by � ;
�� : � is post-multiplied by � ; � is pre-multiplied by � ;
2、DH参数法简介
DH参数法最早是Jacques Denavit与Richard Hartenberg在1955年提出的,常被认为是标准DH参数法(SDH)或者经典DH参数法。SDH参数法因坐标系位置定义的原因(坐标系 {�} 的原点位于关节 �+1 的延长线上),存在一定的缺陷,其后Craig在标准DH参数法的基础上,将坐标系 {�} 的原点放到关节 � 的延长线上,称为改进DH参数法(MDH);后来Hayati在DH参数标定时,又在Craig-MDH参数法的基础上,针对相邻两轴平行或者近似平行的情况下DH参数受平行度误差影响非常大的问题,又进一步提出改进,增加了一个参数 � (SDH与Craig-MDH都是4个参数)。
无论是SDH参数法还是Craig-MDH参数法,都是使用4个参数来表达相邻关节坐标系之间的相对位姿,因此他们都在建坐标系的时候,隐含了强制的空间约束。
- 坐标系原点为关节延长线的交点;
- � 轴沿着关节的轴线方向;
- � 轴为相邻关节轴线的交点(如果两轴延长线相交)或者公垂线(如果两轴延长线不相交);
2.1、SDH参数法
Jacques Denavit与Richard Hartenberg在1955年提出的DH参数法通常被认为是标准DH参数法(Standard-DH)
Denavit, Jacques, and Richard S. Hartenberg. “A kinematic notation for lower-pair mechanisms based on matrices.” (1955): 215-221.
SDH参数法用4个参数描述相邻的关节坐标系之间的关系,如下图所示。值得注意的是,SDH参数法中,坐标系 {�} 的原点位于关节 �+1 的延长线上。
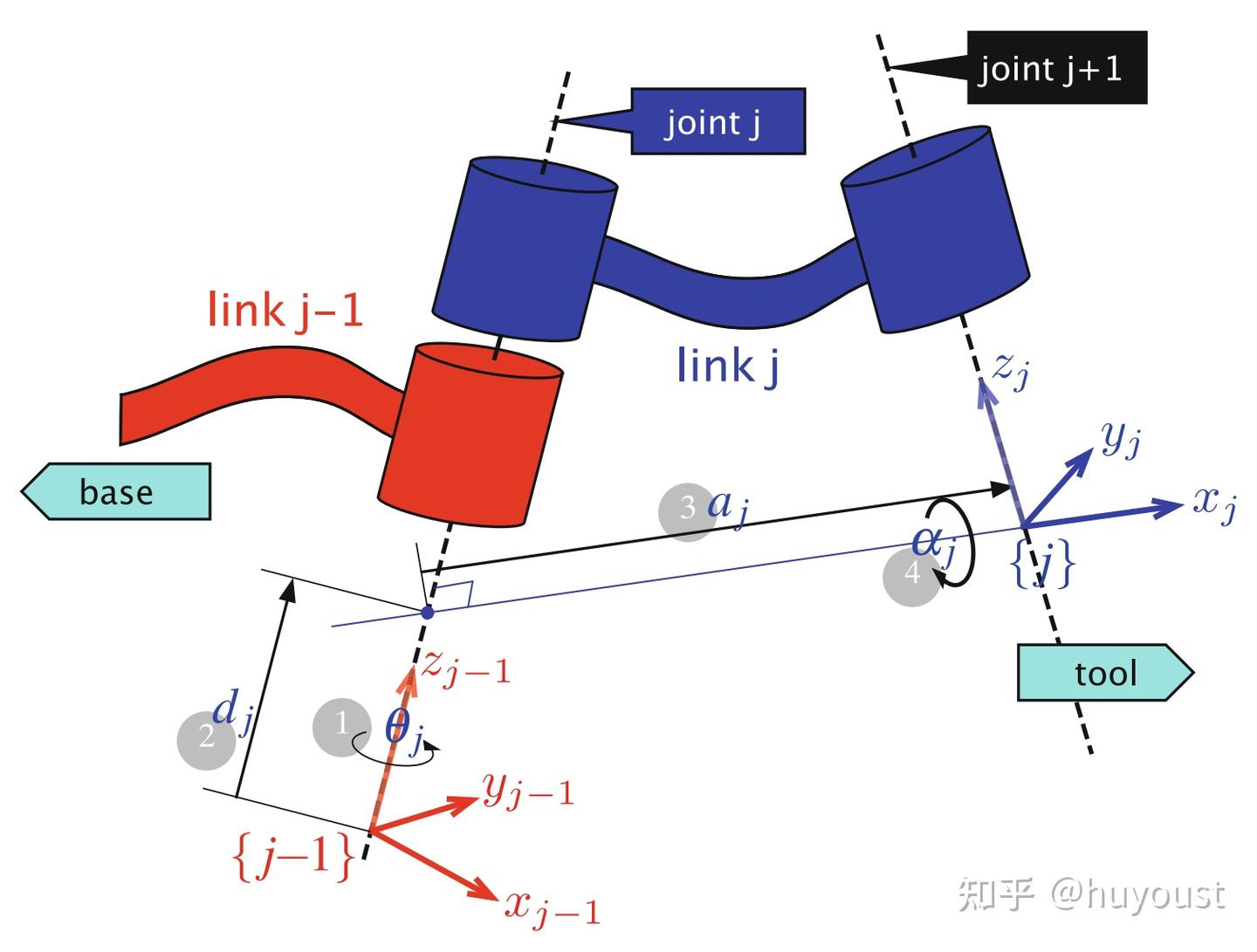
如上图所示,在SDH参数法中,坐标系 {�−1} 经过变换 (1→2)→(3→4) 的顺序(实际上1,2顺序无所谓,3,4顺序也无所谓)得到坐标系 {�} ,注意每一步变换都是相对当前的坐标系(运动的坐标系),应该用右乘:��−1�=��(��)��(��)��(��)��(��)=������(��,��)������(��,��)其中 ��,��,��,�� 分别表示绕 �,� 轴旋转与沿着 �,� 轴平移的齐次( ��(3) )算子。Screw表示平移与旋转的组合变换。
2.2、Craig-MDH参数法
Craig在《机器人导论》一书中提出的DH参数法通常被称为改进DH参数法(Modified-DH)。虽然现在说起MDH参数法通常都是指Craig的MDH参数法,实际上在Craig的MDH参数法基础上还有改进方法,因为为了明确,以Craig-MDH参数法指代Craig在《机器人导论》一书中提出的改进DH参数法。
SDH参数法中,坐标系 {�} 的原点位于关节 �+1 的延长线上(也即连杆 � 的远端),这种建坐标系的方法在处理闭链结构的时候会有歧义,会导致基座上出现两个坐标系。Craig-MDH参数法的主要改进是将坐标系 {�} 的原点放到关节 � 的延长线上(也即连杆 � 的近端)
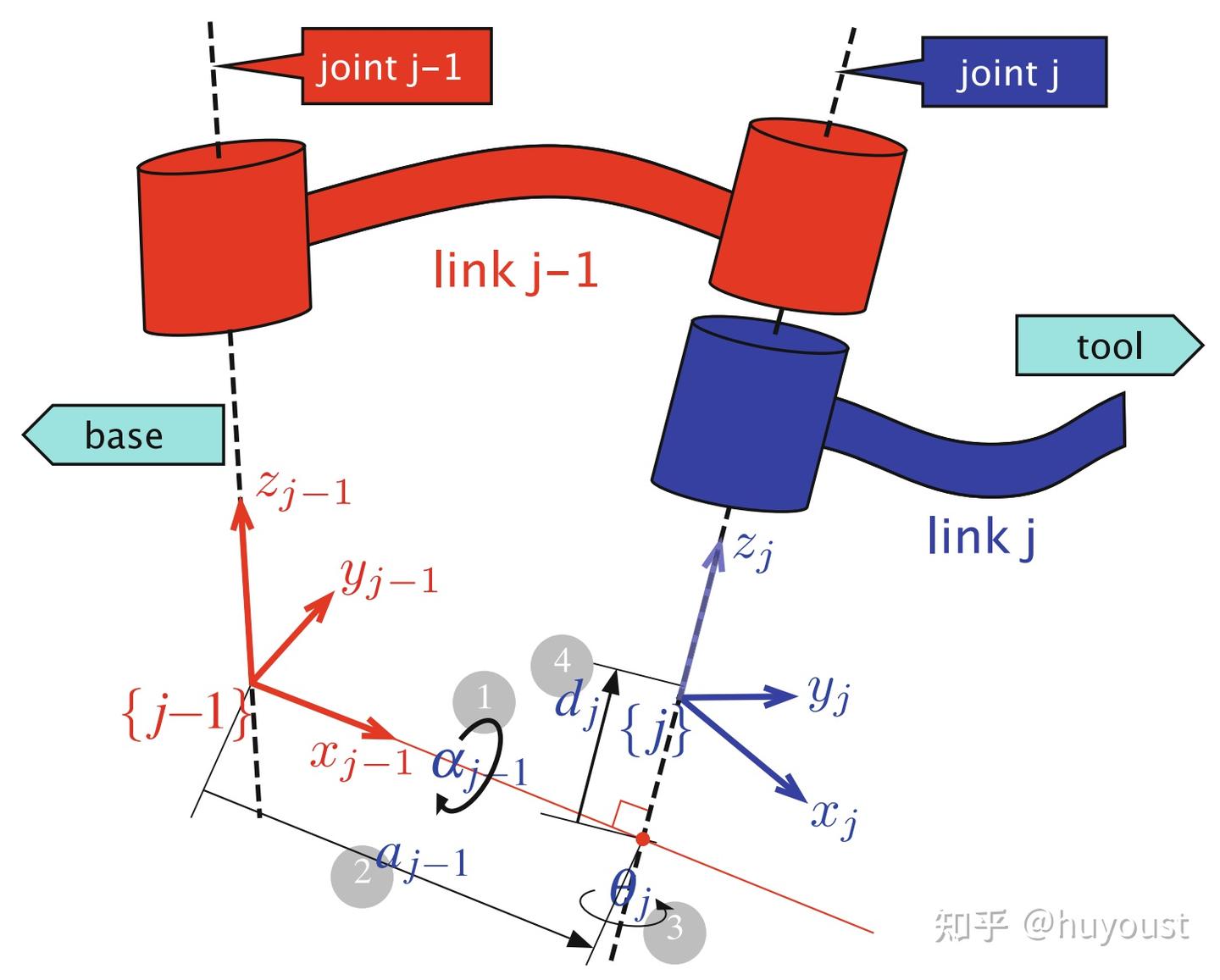
如上图所示,在Craig-MDH参数法中,坐标系 {�−1} 经过变换 (1→2)→(3→4) 的顺序(实际上1,2顺序无所谓,3,4顺序也无所谓)得到坐标系 {�} ,注意每一步变换都是相对当前的坐标系(运动的坐标系),应该用右乘:��−1�=��(��−1)��(��−1)��(��)��(��)=������(��−1,��−1)������(��,��)其中 ��,��,��,�� 分别表示绕 �,� 轴旋转与沿着 �,� 轴平移的齐次( ��(3) )算子。Screw表示平移与旋转的组合变换。在Craig-MDH参数法中比较别扭的一点是参数的下标不统一。
2.3、Hayati-MDH参数法
Hayati-MDH参数法是在Craig-MDH参数法的基础上的改进,用于处理相邻两轴平行或者近似平行时的情况,其主要用处是机器人的几何参数(DH参数)校准/标定。关于这点,感兴趣的可以直接去看原始的论文。
Hayati, Samad, Kam Tso, and Gerald Roston. “Robot geometry calibration.”Proceedings. 1988 IEEE International Conference on Robotics and Automation. IEEE, 1988.
根据Craig-MDH参数法,坐标系的原点需位于相邻关节延长线的交点。如果相邻的两个关节轴平行或者近似平行(对于实际的机械臂,由于加工误差的存在,对于理论设计上平行的相邻关节轴,实际上也可能存在一个微小的夹角),那么两轴之间夹角的微小变化就会导致交点位置的巨大变化,这样得到的DH参数就会很病态,无法反应真实的连杆参数。为了解决这个问题,Hayati等人在处理DH参数校准时,基于Craig-MDH参数法,提出了解决相邻两轴平行或者近似平行时的一种处理办法,即增加一个绕 ��−1 轴的转动角度的额外参数 ��−1,通过 ��−1 的过度,让原本不平行的轴变为平行,然后同样用Craig-MDH参数的方法进行分析,如下图所示:
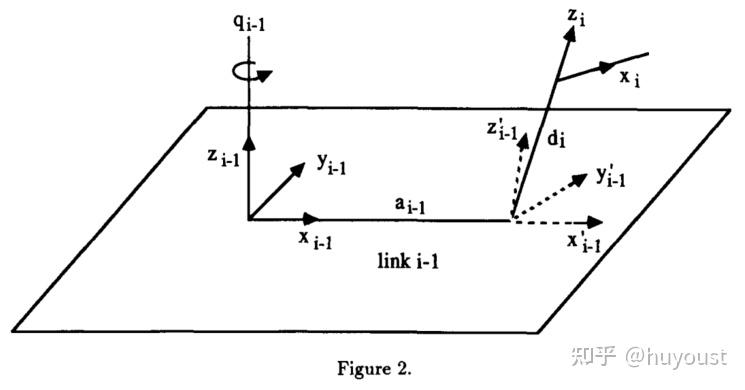
此时,坐标系 {�−1} 到坐标系 {�} 的变换为:��−1�=��(��−1)��(��−1)��(��−1)��(��)��(��)
3、Craig-MDH参数法
此处以Craig的《机器人学导论》一书中介绍的最常用的MDH参数法为例,详细介绍建系步骤与参数提取方法。其它两种方法感兴趣的可以自己整理。
3.1、参数介绍
Craig-MDH参数法用四个参数来描述相邻坐标系的关系,需要注意的是下图中参数的下标:
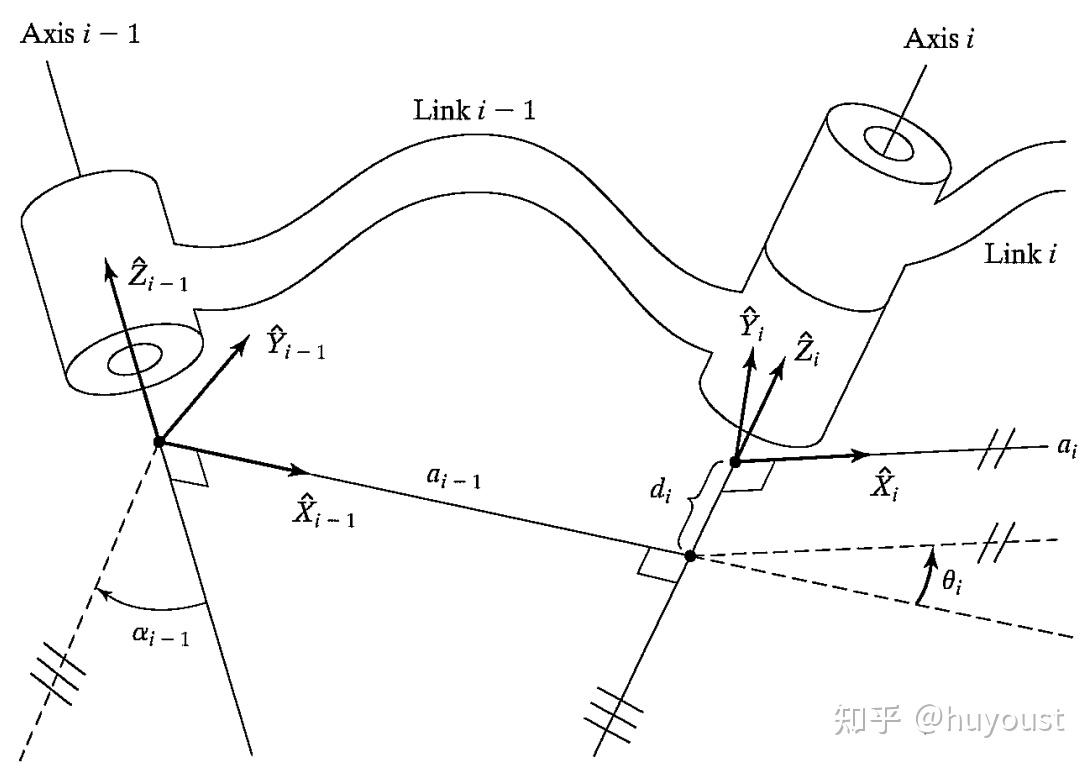
3.2、确定建坐标系的姿态
很多教材中基本都忽略这一步,实际上对于初学者来说,确定建坐标系时的机械臂的姿态也是很重要的。通常我们都是将机械臂的各个关节角设置为零位,以此姿态开始建坐标系分析。实际有些机械臂在零位的时候,并不方便画图建坐标系,例如UR3e的零位为:
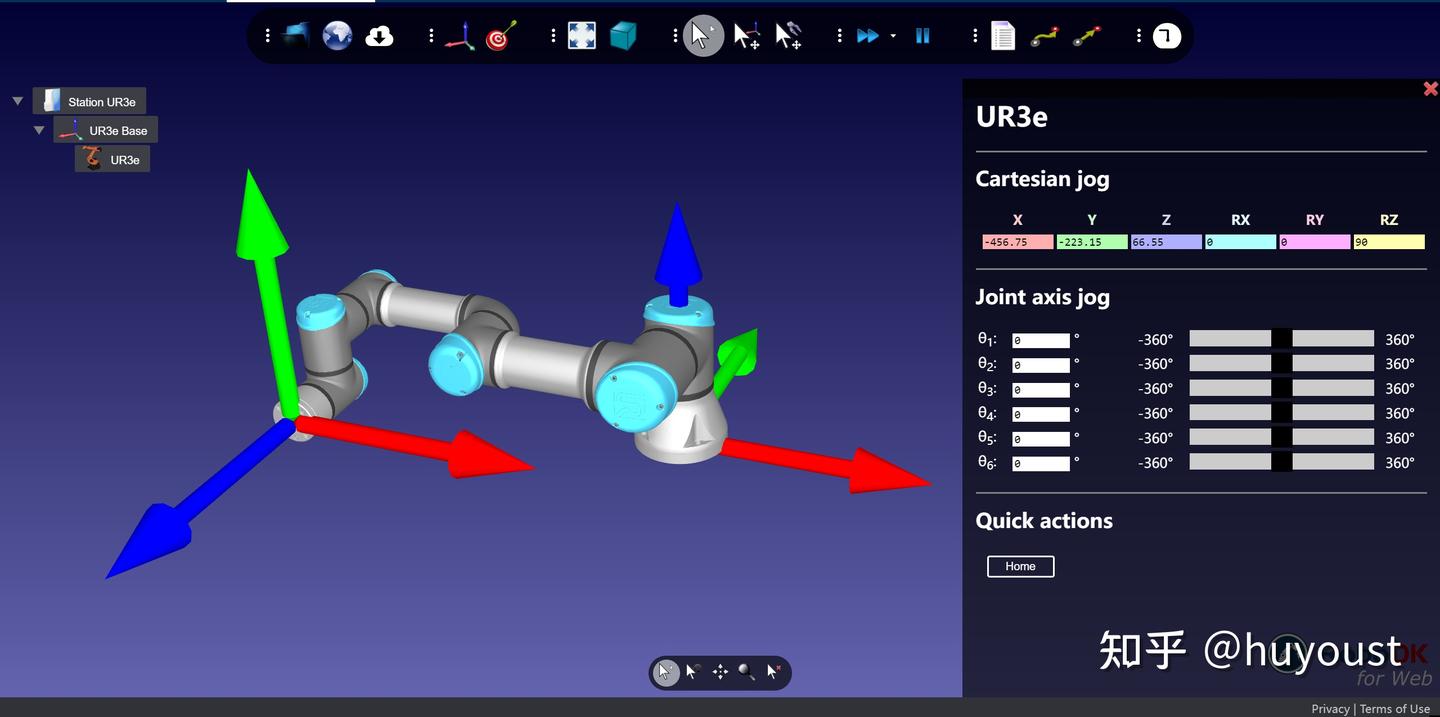
在这个姿势建坐标系,可能并不好看,假如想在它立着,或者默认的HOME姿势下建坐标系

无论选择哪种姿态建坐标系其实都是没关系的,只需在最后实际控制的时候,加上一个关节角的偏置就行。建坐标系的姿势不影响最终的运动学结果,但是确影响DH参数。
3.3、建坐标系
Craig-MDH参数法有严格的建系标准,不能随意设置坐标系的原点以及 ��� 轴,需严格按照规定来建,这也是MDH参数法包括SDH参数法总为人所诟病的原因之一。实际上对于初学者,很难准确分析出任给的一个机械臂的DH参数,哪怕是熟练掌握的人,也常常需要对照参考书一步步分析。当然,再怎么复杂,对于一个机械臂建坐标系,分析DH参数也只需要最开始的一次。
(1)确定建坐标系的姿态
这里选择这种位姿建坐标系
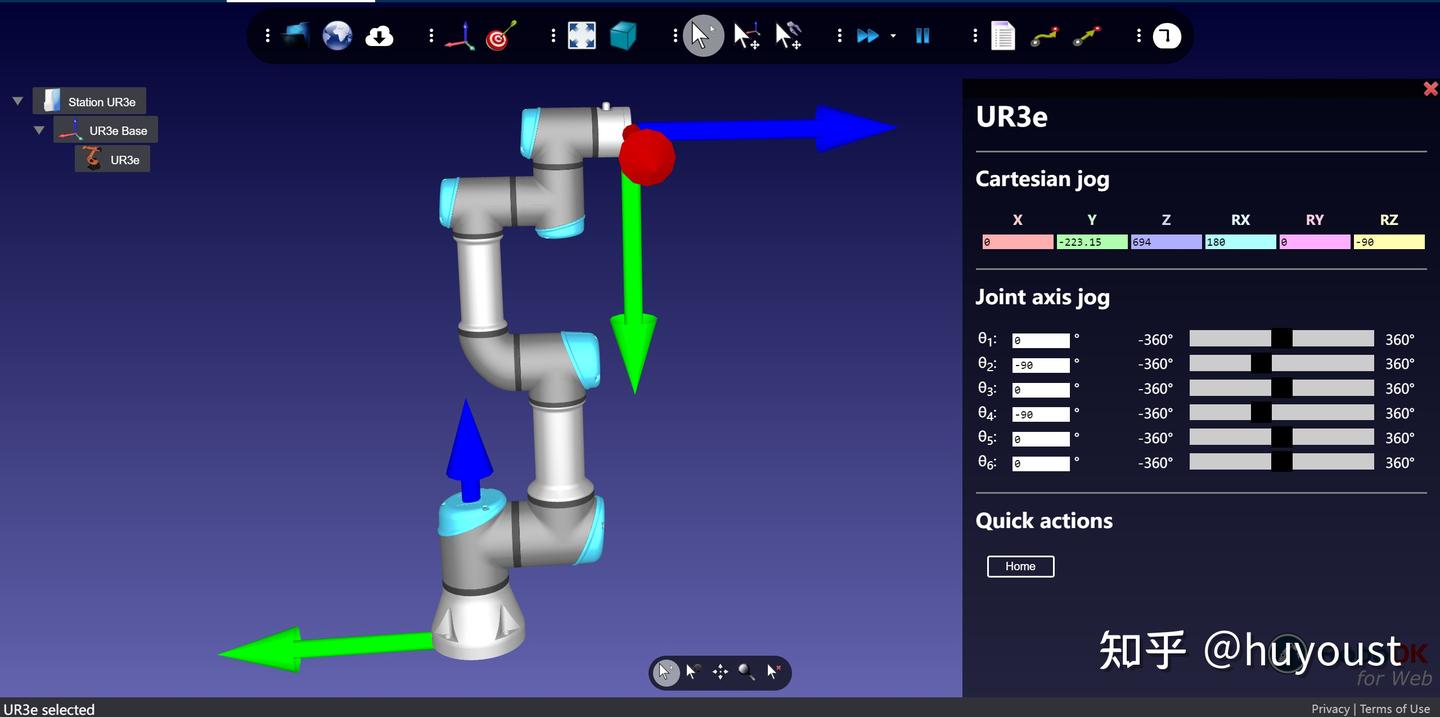
(2)Craig-MDH参数法建系步骤
- 强制要求:找出各关节轴的轴线,并沿着各关节轴的轴线画延长线;
- 强制要求:画出相邻两轴(轴 � 与轴 �+1 )的公垂线(两轴异面或平行)或者交点(两轴相交),以轴 � 与轴 �+1 的交点或者公垂线与关节轴 � 的交点作为坐标系 {�} 的原点;(此处如果轴 � 与轴 �+1 平行,公垂线有无数条,通常选择过前一个坐标系原点的那条公垂线,但是非强制规定)
- 强制要求:规定 �� 沿着关节轴 � 的轴线方向(此处 �� 的朝向没有强制规定,有两种选择)
- 强制要求:规定 �� 沿着公垂线指向,如果轴 � 与轴 �+1 相交,规定�� 垂直于轴 � 与轴 �+1 所在平面(此处�� 的方向没有强制规定,有两种选择)
- 强制要求:按照右手定则确定��
- 非强制要求:当第一个关节变量(即转动关节的角度或者平动关机的位移)为0时,规定坐标系 {0} 与 {1} 重合(此处非MDH方法的强制规定,而是约定俗成),坐标系 {�} 不做规定。
按照上面的步骤就可以逐步确定坐标系:
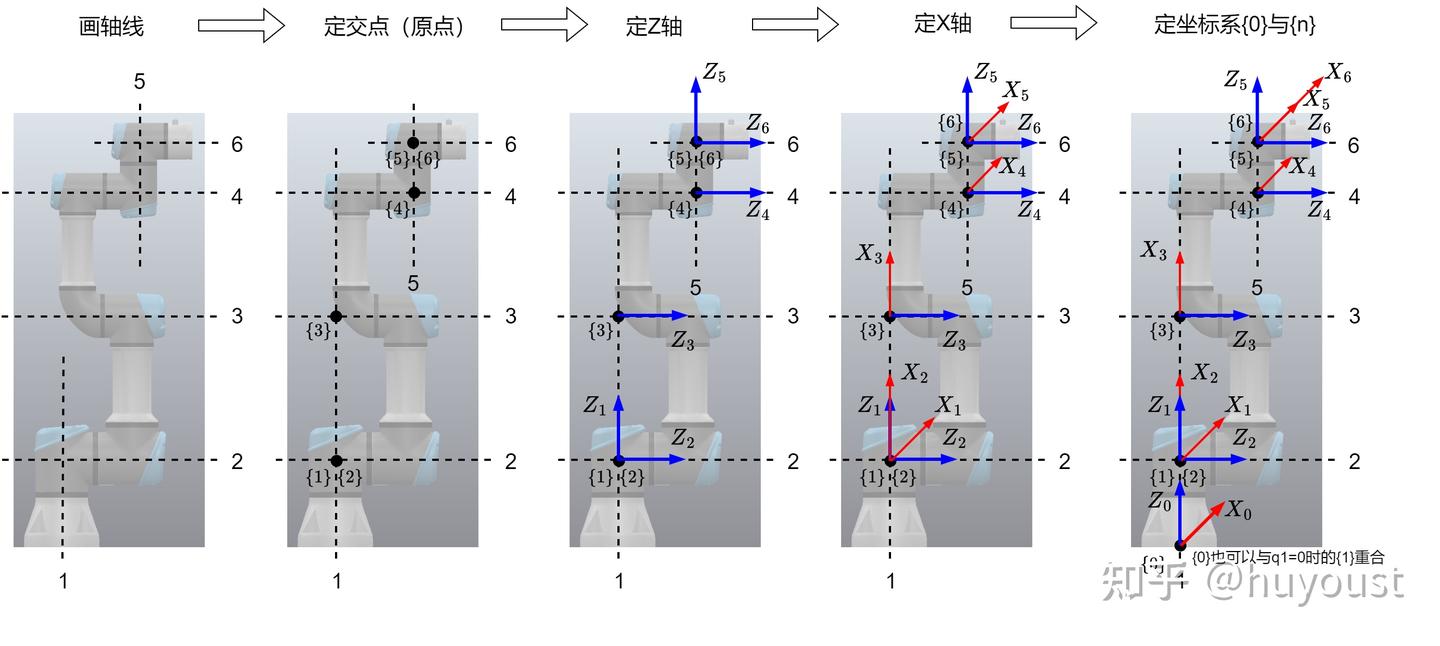
这里实际上也隐藏了一个细节,那就是选择用于建坐标系的姿态,通常都是选择机械臂的关节角为零位时建立坐标系,但是这个不是强制要求的。如果建立坐标系时机械臂的关节不在零位,那么实际分析时给关节变量减去/加上偏置量即可。
而且MDH参数法建坐标系并非唯一,相应的MDH参数表也并非唯一
3.4、提取MDH参数表
Craig-MDH参数法中,四个参数的定义如下:
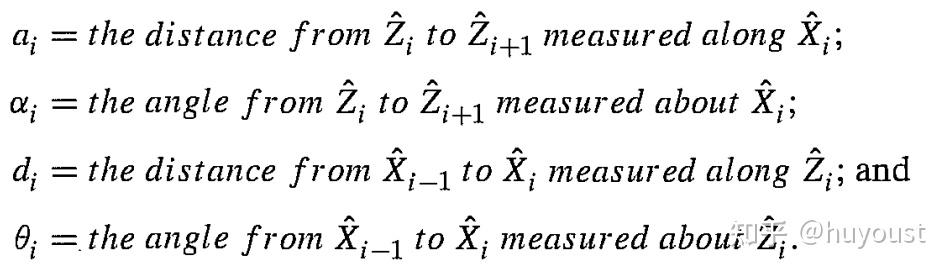
根据MDH参数的定义,与上图坐标系对应的MDH参数表如下,需要注意的是MDH参数表中, �,� 的下标为 �−1 ,而 �,� 的下标为 � 。
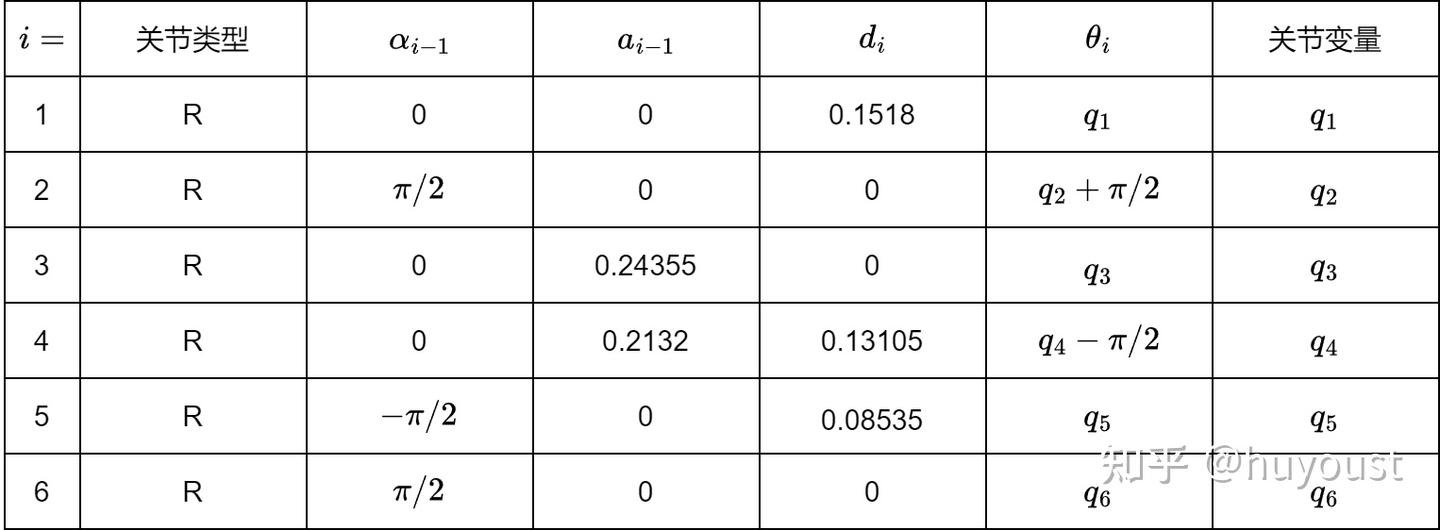
根据坐标系分析的��,�� 只是当前姿态下的值,也叫偏置值,需要根据对应的关节类型加上关节变量值。对于转动关节 ��:=��+�� ,对于移动关节 ��:=��+�� 。
3.5、转移矩阵通式
由于前面的建立坐标系的约束条件以及相应的DH参数的约定对任意两个相邻的坐标系都是一样的,因此如果按照Craig-MDH参数法进行建系与参数提取,坐标系 {�−1} 与坐标系 {�} 之间就存在通式。按照连续变换的链式法则以及Craig-MDH参数法中各参数的含义,可以得到转移矩阵的通式为:��−1�(��)=��(��−1)��(��−1)��(��)��(��)其中 ��,��,��,�� 分别表示绕 �,� 轴旋转与沿着 �,� 轴平移的算子。
3.6、根据链式法则计算正运动学
写出 ��−1� 后,就可以根据连续变换的链式法则计算末端连杆坐标系相对于基坐标系的位姿:�0�(�1,�2,⋯,��)=10�(�1)21�(�2)⋯��−1�(��)
3.7、编程验证
用Peter-Corker的机器人工具箱看一下MDH参数是否正确,也可以对比一下SDH参数法的结果。关于Peter-Corker的机器人工具箱的使用可以参考系列教程:
huyoust:Peter Corke机器人工具箱简明教程:(1)下载与安装
huyoust:Peter Corke机器人工具箱简明教程:(2)Matlab中的函数优先级
huyoust:Peter Corke机器人工具箱简明教程:(3)串联机械臂的建模与可视化(以UR3e机械臂为例)
huyoust:Peter Corke机器人工具箱简明教程:(4)串联机械臂的运动学分析(以UR3e机械臂为例)
huyoust:Peter Corke机器人工具箱简明教程:(5)串联机械臂的轨迹规划之基础概念
huyoust:Peter Corke机器人工具箱简明教程:(6)串联机械臂的轨迹规划
huyoust:Peter Corke机器人工具箱简明教程:(7)雅可比矩阵
L1 = 0.15185;
L2 = 0.24335;
L3 = 0.13105;
L4 = 0.2132;
L5 = 0.08535;
L(1) = Revolute('d', L1, 'a', 0, 'alpha', 0, 'offset', 0);
L(2) = Revolute('d', 0, 'a', 0, 'alpha', pi/2, 'offset', pi/2);
L(3) = Revolute('d', 0, 'a', L2, 'alpha', 0, 'offset', 0);
L(4) = Revolute('d', L3, 'a', L4, 'alpha', 0, 'offset', -pi/2);
L(5) = Revolute('d', L5, 'a', 0, 'alpha', -pi/2, 'offset', 0);
L(6) = Revolute('d', 0, 'a', 0, 'alpha', pi/2, 'offset', 0);
L(1).mdh = 1;
L(2).mdh = 1;
L(3).mdh = 1;
L(4).mdh = 1;
L(5).mdh = 1;
L(6).mdh = 1;
ur3e = SerialLink(L, 'name', 'UR3e')
关节示教模式下看一下可以看到是没问题的,与建系时的姿势以及坐标系都是符合的:
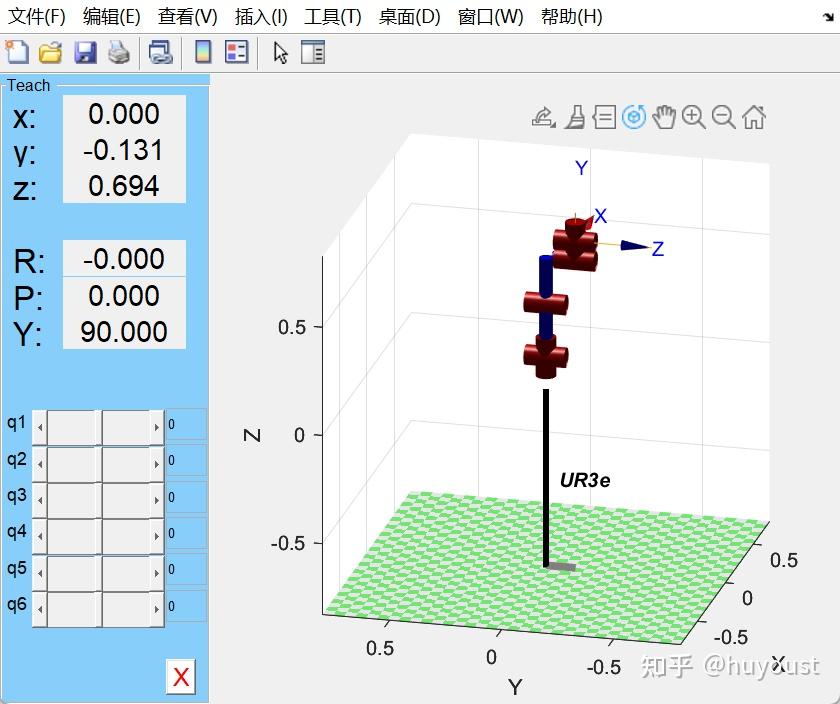





评论0