来源:https://zhuanlan.zhihu.com/p/624359553
通过前面的章节我们已经完成了对六自由度机械臂的运动学以及轨迹规划研究,但在过程中并没有考虑到力对机械臂的作用,也并没有考虑机械臂各关节以及末端执行器的运行速度,所以控制精度并不高。
在后续的几个章节中,我们开始研究机械臂的微分运动学及其静力学,并在最后,阐明建立在速度和力可操纵性椭球(manipulability ellipsoid)定义基础之上的运动静力学二元性的概念。
我们研究微分运动学的目的便是找到关节速度与末端执行器的角、线速度之间的映射关系,而几何雅可比矩阵(Geometric Jacobianmatrix)便是用于描述这种映射关系的矩阵。
一、概述及回顾
根据前面的章节我们不难得出n自由度机械臂的正运动学方程为:
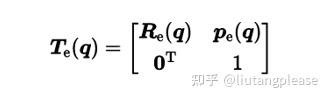
其中,q是1×n的关节变量向量。
微分运动学的目的,是寻找关节速度与末端执行器线速度和角速度之间的关系,也就是将末端执行器的线、角速度表示为一个关节速度的函数。
首先说明变量含义:

我们将末端执行器的线、角速度与关节变量之间的线性关系表示为:
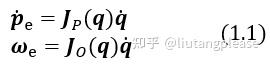
紧凑形式可表示为:
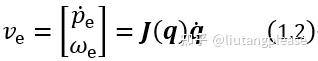
式1.2即为机械臂的微分运动学方程,其中的6×n矩阵J即为机械臂的几何雅可比矩阵:
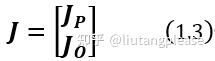
二、旋转矩阵求导
式(1.1)的机械手正运动学方程以位置向量和旋转矩阵关于关节变量的函数的形式描述了末端执行器的位姿。
为了表征末端执行器的线速度和角速度,首先需要考虑旋转矩阵关于时间的导数。
考虑时变的旋转矩阵 R=R(t)。鉴于R的正交性,有下述关系(1.4)
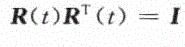
将上式对时间求导,得到以下特性(1.5)
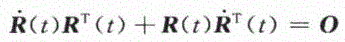
令(1.6)
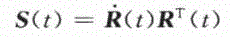
由于(1.7)

故S为(3x 3)反对称矩阵。
进而,我们可以通过在式1.6两侧同时右乘R(t)得到
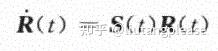
这使得R(t)对时间的导数可以表示为R(t)自身的函数
上式通过反对称算子S,将旋转矩阵R(t)与其导数联系起来,具有深刻的物理意义。





评论0