来源:https://zhuanlan.zhihu.com/p/390510359
本文参考了The Constructs 平台的课程,如有侵权,请联系我删除
The Construct: A Platform to Learn ROS-based Advanced Robotics Onlinewww.theconstructsim.com/
正文
当我们谈到机械臂的运动学的时候,我们自然的会想到机械臂在空间中做各种运动,但是什么是机械臂运动学?
运动学通常描述的是点的运动,刚体或者物体的运动,以及一个刚体系统的运动,并且这些运动的描述都不考虑造成这个运动的力和力矩
一个机器人的动力学结构通常由一个个的links来描述,这些links也就是之前提到的刚体
Joint用来连接两个相邻的links,并且对它们的相对运动做一个约束
这个结构被称为Kinematic Chain
某一个时刻的机器人的位姿可以用以下的两种方式来描述:
- 一个包含每个运动关节(joint)的列表,通常是相对于零位的角度或者平移的距离
- 对机械臂的每个刚体在世界坐标系中的描述,比如:用一个矩阵来描述机械臂的1,2,3轴相对于世界坐标的位姿
其中第一个方式提到的运动关节的角度列表被称为机器人的配置(Configuration of robot)
机械臂所处的世界称为工作空间(Workspace)
在更深入ROS机械臂运动学之前,需要明确几个定义
参考系(Frame of reference)
在Gazebo的仿真环境中,我们需要定义机械臂的参考坐标,一个三维的xyz坐标系
比如在下面的机械臂,把base_link作为参考系
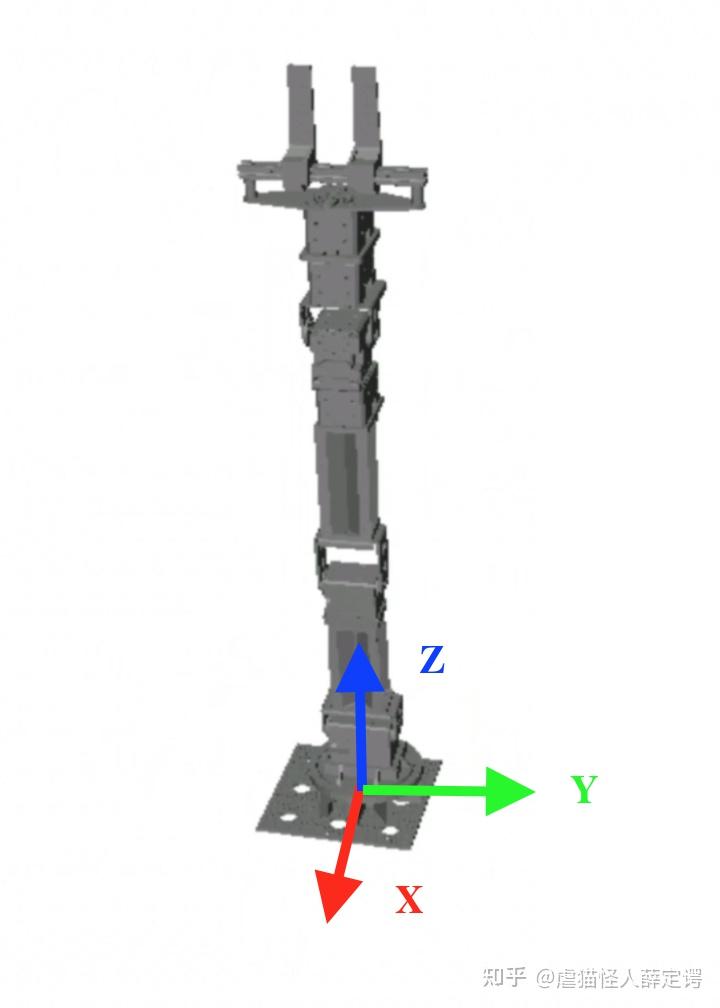
位置的描述
点P相对于随机的一个原点O的位置可以由笛卡尔坐标系的xyz坐标表示
用下面的代码可以在Gazebo中生成一个可乐罐
import math, rospy
from utilities import set_model_state, get_model_state, \
spawn_coke_can
from geometry_msgs.msg import Pose, Point, Quaternion
if get_model_state('coke_can').success == False:
spawn_coke_can('coke_can', Pose(position=Point(0,1,0.22)))
可以看到spawn_coke_can这个函数需要输入两个参数
第一个是物体的唯一名称
第二个是物体出现的位置坐标,这个坐标被封装在Pose类中,可以看到可乐罐被放在距离机械臂Y方向1米的地方
P = [0,1,0.22]注意这里Z方向0.22是因为可乐罐本身的重心在Z方向的0.22处
可以用下面的代码查看可乐罐的当前位置信息
model_state = get_model_state('coke_can')
print (model_state.pose.position)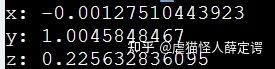
不过由于Gazebo物理引擎添加了环境噪声,所以XYZ的值和设置的值由些许不同
如果把Z的值设置的大于0.22,比如设置为1,由于Gazebo环境重力的影响,可乐罐会掉落在地面
new_pose = Pose(position=Point(1,0,1))
set_model_state('coke_can', new_pose)
旋转的描述
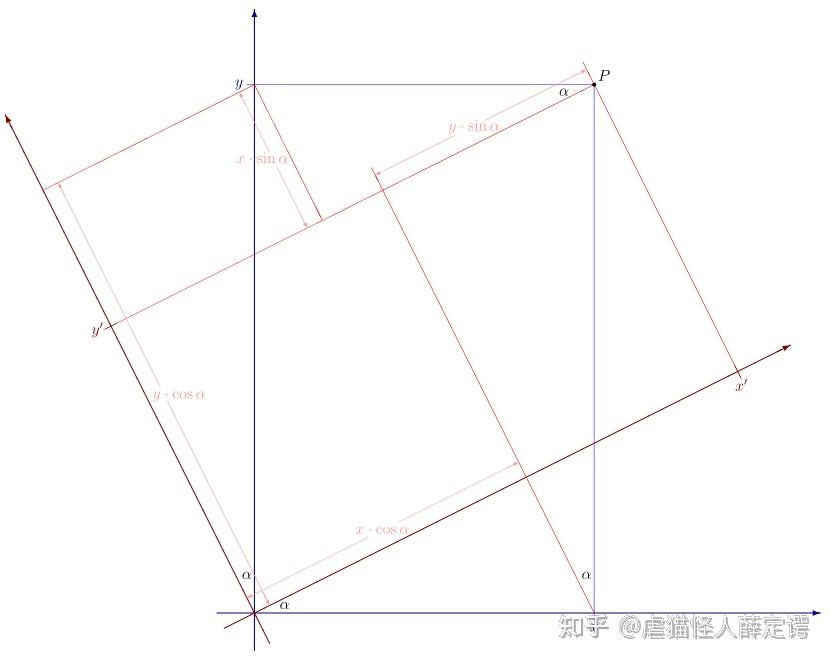
两个刚体相对的位置和旋转关系可以用两个刚体上的坐标系关系表示
在2维的情况下,两个参考系的旋转角为 ,那么这两个坐标系的相对关系如下

使用下面的代码可以让之前的可乐罐绕机械臂旋转
import math, rospy
from utilities import set_model_state, get_model_state
from geometry_msgs.msg import Pose, Point, Quaternion
x, y, z = 1, 0, 0.22
for angle in range(0,360,10):
theta = math.radians(angle)
xp = x * math.cos(theta) - y * math.sin(theta)
yp = x * math.sin(theta) + y * math.cos(theta)
set_model_state('coke_can', Pose(position=Point(xp,yp,z)))
rospy.sleep(0.1)
平面的旋转相当于绕Z轴旋转,旋转矩阵如下

绕X和Y轴的旋转矩阵如下
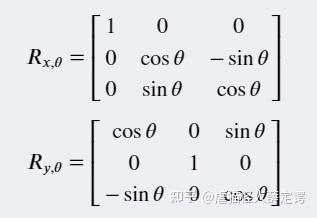
在ROS中,旋转的表述并不是用旋转矩阵来表示,而是用四元数(Quaternions)
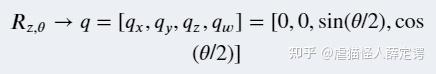
在ROS中,TF提供了计算四元数的函数
tf.transformations.quaternion_about_axis(angle, axis)angle是旋转角度的弧度,axis是一个3D的向量
import math, rospy
from utilities import set_model_state, get_model_state, \
pause_physics, unpause_physics
from geometry_msgs.msg import Pose, Point, Quaternion
from tf.transformations import quaternion_about_axis
pause_physics()
position = Point(x=0.5, y=0, z=0.5)
for angle in range(0,360,10):
theta = math.radians(angle)
q = quaternion_about_axis(theta, (0,0,1))
orientation = Quaternion(*q)
set_model_state('coke_can', Pose(position, orientation))
rospy.sleep(0.1)用上面的代码可以让可乐罐绕z轴旋转

绕X和Y轴旋转的四元数如下

旋转参数化
欧拉角

欧拉角由α, β, γ组成
原始坐标系为蓝色,各个轴为小写的xyz
旋转坐标系为红丝,各个轴为大写的XYZ
旋转关系可以由下面三个角度确定
- Rotate about the z-axis by the angle α
- Rotate about the current x-axis by the angle β
- Rotate about the current z-axis by the angle
RPY角
旋转可以由Roll,Pitch,Yaw三个角度确定
RPY三个角度的定义和上面提到的欧拉角类似,不同点在于,RPY角度是相对于三个不同轴的x-y-z旋转,而欧拉角的第一轴和第三轴可以是相同的轴比如z-x-z
变换矩阵
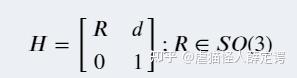
变换矩阵会把旋转和平移矩阵结合起来,变换矩阵能够很大程度的加速计算机的计算
然而在ROS中,由于四元数替代了旋转矩阵,ROS会用另外一种数据结构Pose

Links&Joints
Links为刚体,用Joints来连接
Joint可以被分为三类
- Revolute: the attached links rotate about a common axis.
- Prismatic: the attached links translate about a common axis.
- Spherical: the attached links rotate about a point.
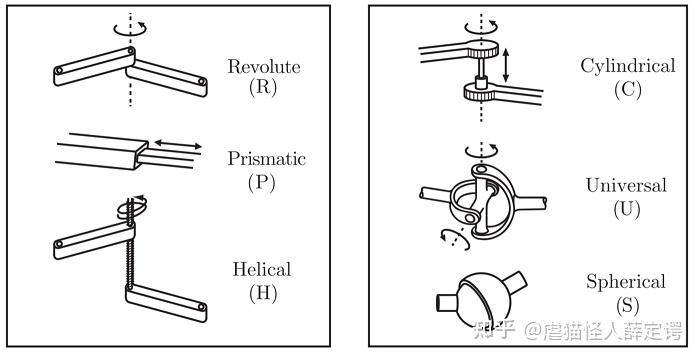
机械臂结构

这个机械臂的坐标系可以定义为
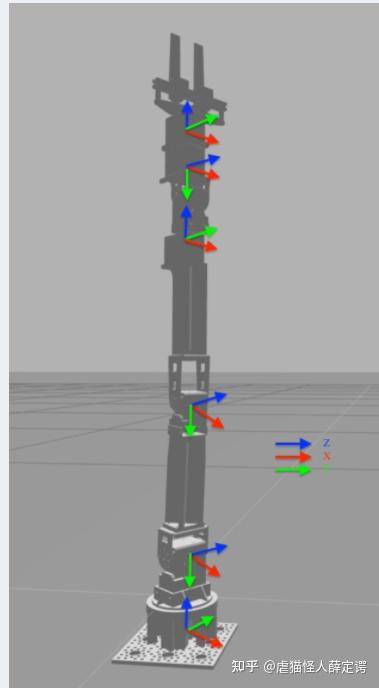







Joint limits
大多数的关节都会有上限下限

URDF
ROS中定义了一种URDF(Universal Robot Description Format)文件类型,用来描述机械臂
定义各个关节的质量,关节范围,几何形状等等,语法为XML语法
<robot name="my_robot">
<link name="base_link">
...
</link>
<link name="link_1">
...
</link>
<link name="link_2">
...
</link>
<joint name="joint_1" type="revolute">
...
<parent link="base_link"/>
<child link="link_1"/>
</joint>
<joint name="joint_2" type="revolute">
...
<parent link="link_1"/>
<child link="link_2"/>
</joint>
</robot>在link元素里面,包含了三个子元素
<link name="link_1">
<visual>
<origin xyz="0 0 0" rpy="0 1.5708 0" />
<geometry>
<cylinder length="1" radius="0.1"/>
</geometry>
<material name="grey">
<color rgba="0.6 0.6 .6 1"/>
</material>
</visual>
<collision>
<origin xyz="0 0 0" rpy="0 1.5708 0" />
<geometry>
<cylinder length="1.0" radius="0.1"/>
</geometry>
</collision>
<inertial>
<mass value="2.0"/>
<inertia ixx="0.2" ixy="0.0" ixz="0.0" iyy="0.6" iyz="0.0" izz="0.6"/>
</inertial>
</link>Visual标签用来记录可视化的参数,位置,颜色,形状等
Collision标签用来记录碰撞矩阵,用来做物理仿真
Inertia标签用来记录旋转的惯量
Joint元素用来定义Link之间的连接
<joint name="joint_2" type="revolute">
<origin xyz="1 0 0" rpy="0 0 0"/>
<axis xyz="0 1 0"/>
<parent link="link_1" />
<child link="link_2" />
</joint>RVIZ
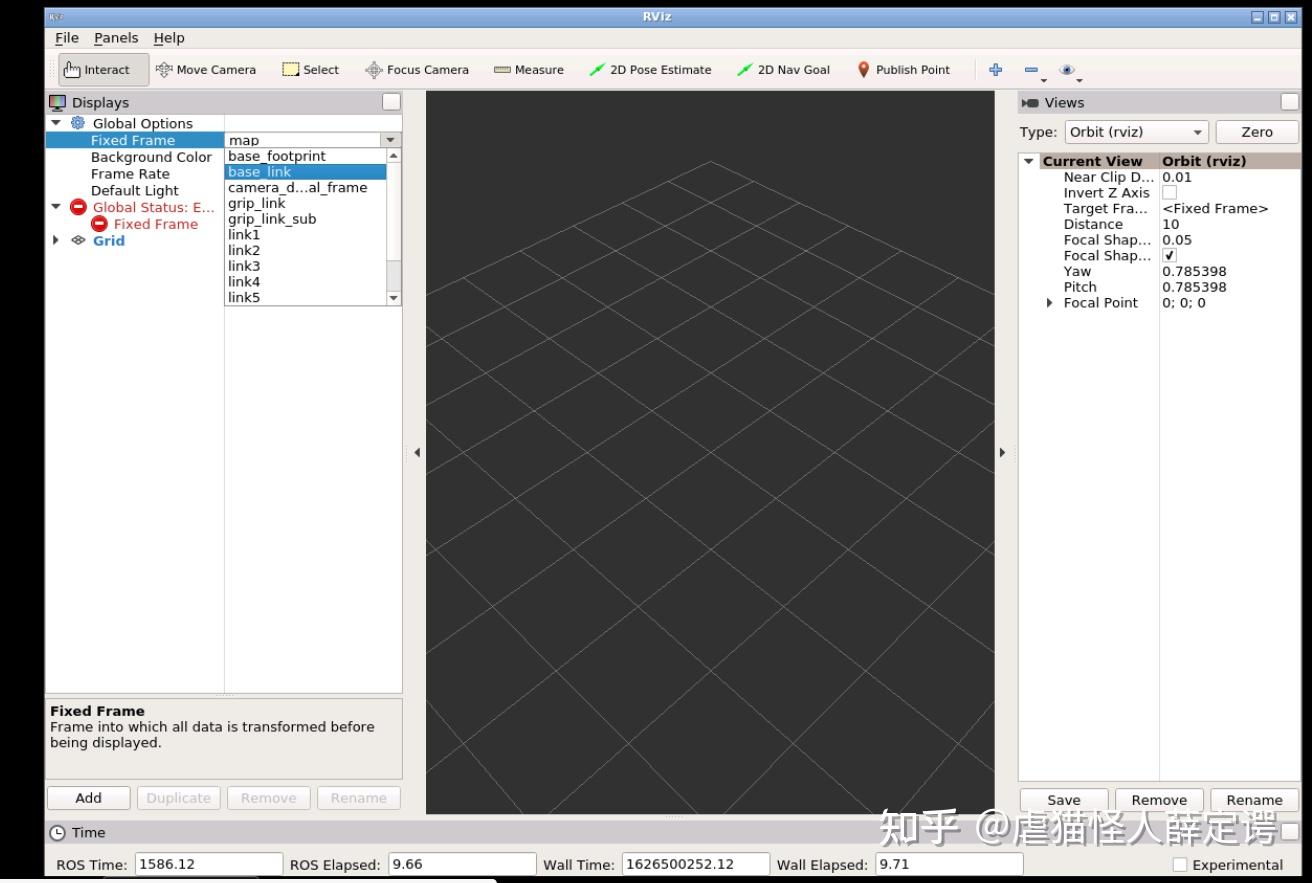
使用URDF描述好一个机器人之后,可以用Rviz工具进行可视化
把Fixed frame设置为Base_link
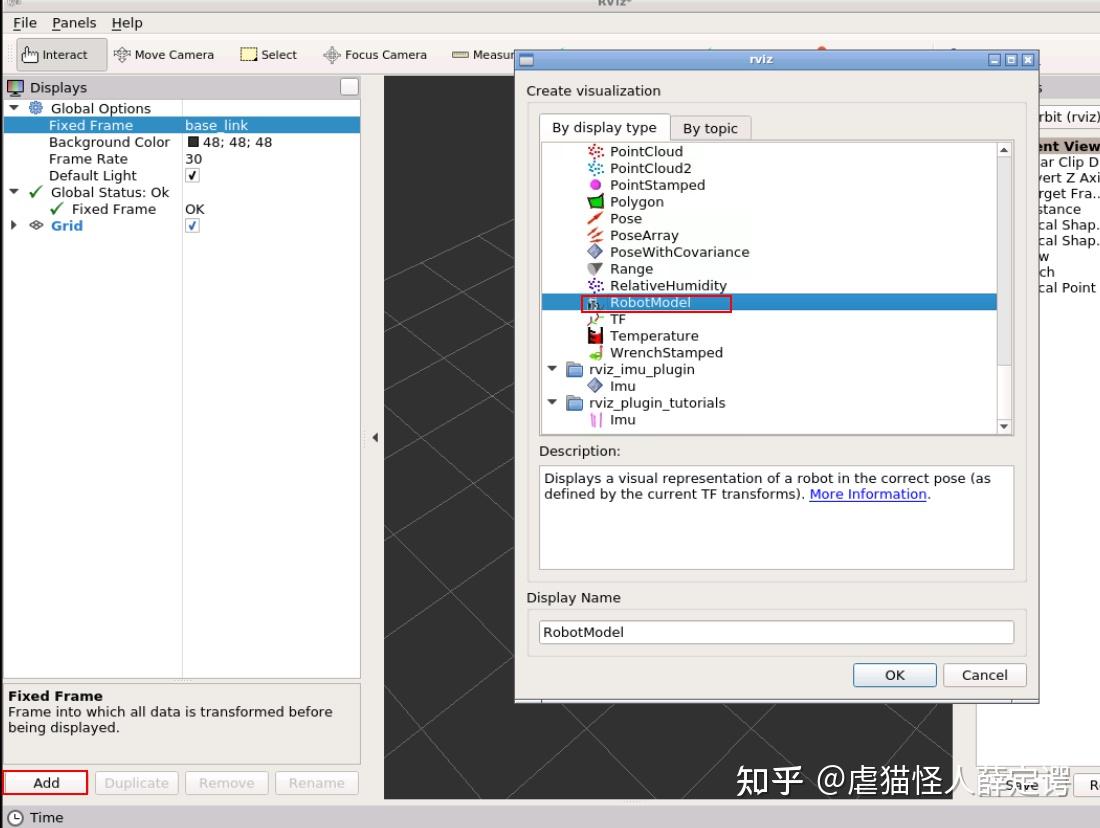
添加一个robotmodel
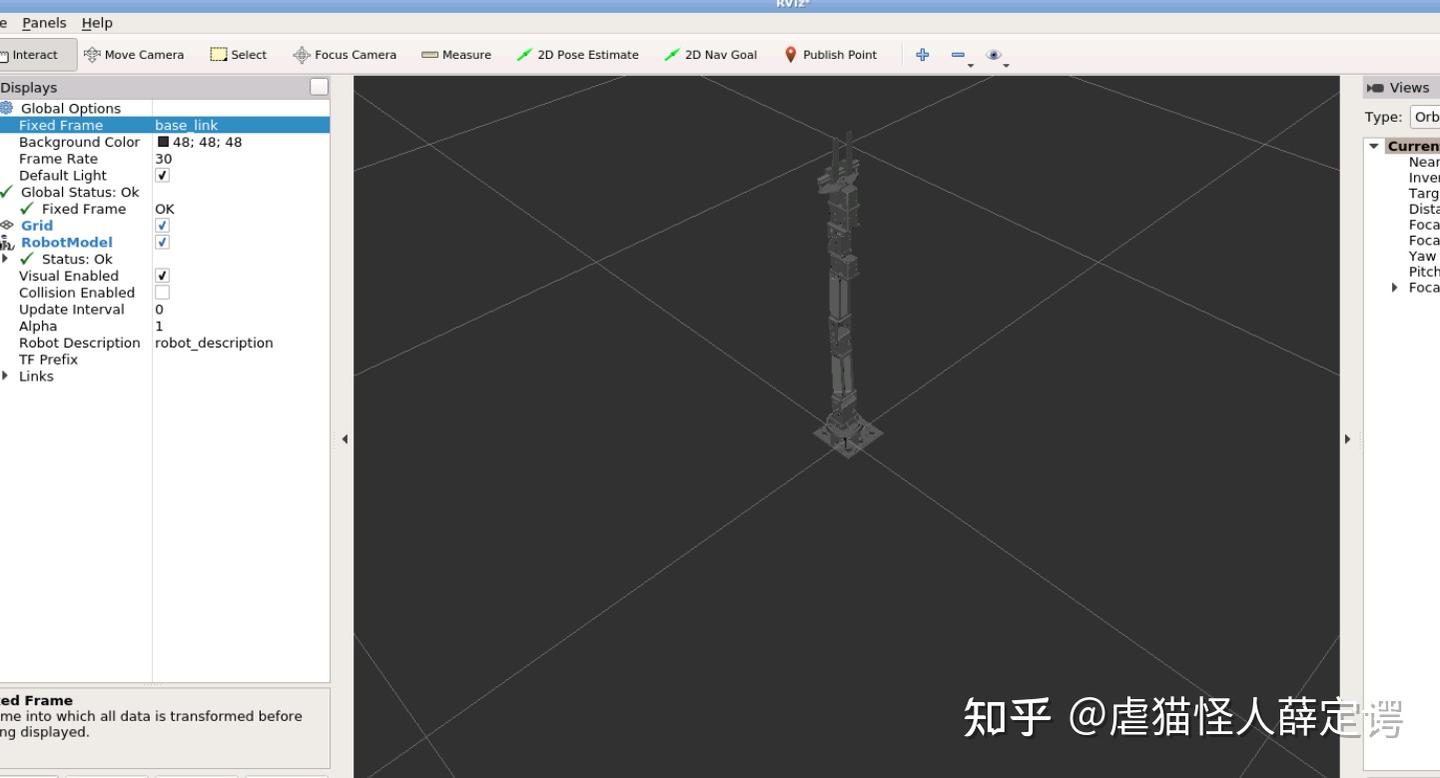





评论0