来源:https://zhuanlan.zhihu.com/p/691136933
协作机械臂系列包括协作机械臂的发展概述、构型、结构、运动学、运动规划、视觉、多机协同、ROS操作系统、场景应用、工程实践共十节内容,本篇为第一节:协作机械臂的发展概述。
1 协作机械臂定义
1.1 机器人概念
机器人这一概念源自1920年捷克作家的《Rossum’s Universal Robots》剧本,剧本中构想的机器人是一种具有类人特性的异种生命体,这被视为现代机器人的想法起源。
1962年,美国阿贡国家能源实验室为了解决核污染机械操作问题,研制出遥控操作机械手处理放射性物质。同一时期,德沃尔制造“工业机械臂”用于汽车产线上的装配工作。这种“工业机械臂”的萌生掀开了机器人发展的序幕。然而,在资本市场的加持下,机器人的概念开始泛化,只要具备有目的的行为机器,都可以称之为机器人。
我认为机器人的标准定义应当至少包含这三个条件:
· 具有脑、手、腿功能:靠手实现操作,靠腿实现移动,靠脑实现控制;
· 具有多传感系统:用于识别外界环境和自身状态;
· 具有交互能力:与人或生物的自主交互、与周边环境、设施的自主交互。
而像常说的工业机器人,严格来说应该称为工业机械臂。概念的界定似乎显得无足轻重,但清晰的概念界定往往能够引导技术发展方向。因此下文市面上常称为协作机器人的技术或产品,我统一使用“协作机械臂”称呼,算是一点技术人员的执著吧。
1.2 协作机械臂的概念
协作机械臂的概念是1996年由美国西北大学两位教授Michael Peshkin和 Edward Colgate首次提出[1],他们在通用汽车装配现场,发现在驾驶中要将重达 22 磅的加热和冷却设备放入仪表板的开口中,很快就疲惫了且容易损伤腰背,便提出希望有一种机器,目的不是取代工人,而是帮助他更有效地完成工作,降低被解雇、受伤的风险,这种装置也被通用称为智能协助装置(Intelligent acid device,IAD)。1997年,“Cobot”这一概念正式以专利[2]的形式发表,协作机械臂概念诞生。

协作机械臂(collaborative robot,简称Cobot或者Co-robot)衍生于传统工业机械臂,是以“消除安全围栏”、“关节一体化”、“拖动编程示教”为核心特点的互补型机械臂,其借助传感器和算法实现力感知功能,加以轻量化、降低运动速度、限制电机功率的方式来确保人机协作的安全性,但也同时带来了速度低、刚度低、负载低、精度低等缺点,相比而言,工业机械臂更适合工作效率、可靠性更高的场合,协作机械臂更适合人机安全、可编程性要求高的场合。
1.3 人机协作概念
“协作”的概念不是指协作机械臂与人之间的协作,因为现在的机械臂无法独立完成任务,必须安装适当的末端工具,增加必要的外部辅助设施以构成机械臂工作站才能正常工作,因此“协作”的概念指的是机械臂系统与人之间的协作。机械臂系统的概念包括机械臂、末端执行器/工具、用于支持机械臂完成任务的其他传感器、设备、机械设施等。
ISO 10566中[3]将人机协作的安全性分为四个方面:
(a)监控级(Safety-rated monitored stop):监控到人进入协作区域——机器停止工作——监控到人离开协作区域——机器恢复工作
(b)拖动级(Hand guiding):人拿起拖动控制装置——机器停止工作——人拖动机器工作——人释放拖动控制装置——机器恢复自动工作
(c)保距级(Speed and separation monitoring):人与机器同时在协作区域工作,但人与机器之间保持最小距离,当超过规定的最小距离时,机器触发保护功能,停止工作;
(d)限能级(Power and force limiting):对机械臂输出的功率和力进行限制。
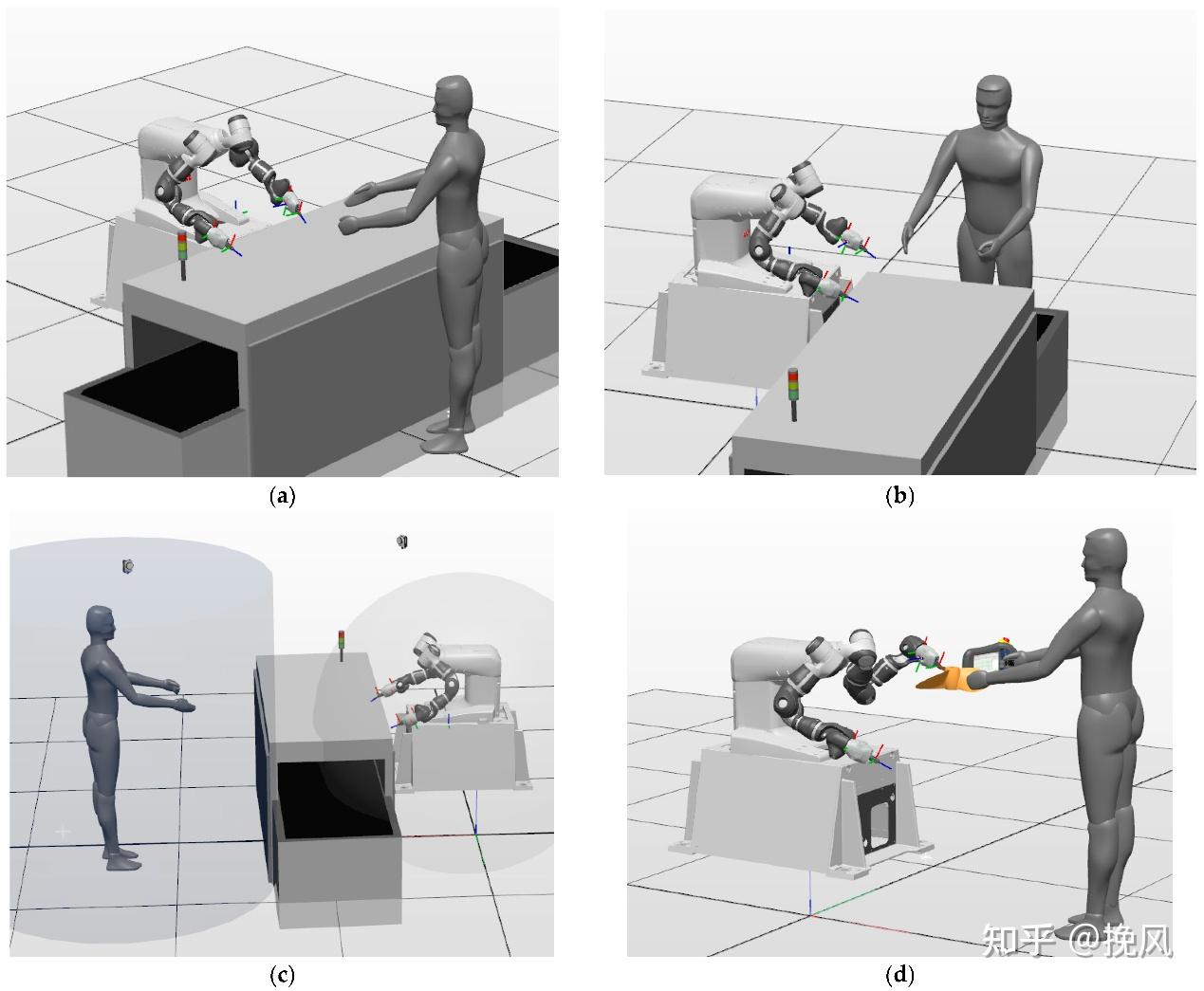
当前协作机械臂本体的主流方案即上述人机协作的(d)项,从根源上避免伤害事件的发生。
2 协作机械臂的发展史
2005年,欧盟第六框架计划资助的中小型企业(SME robot)项目开始实施,旨在通过机械臂技术增强中小型企业劳动力水平,在该背景下,Universal Robots在丹麦大学创办成立,并于2008年生产出世界上第一款从产品设计伊始就以协作机械臂要求进行开发的协作产品UR5,消除了对安全围栏的需求;2015年Universal Robots推出世界上首台桌面协作机械臂UR3。
2008年,为了帮助美国本土的SMEs提高生产效率,Heartland Robotics(2012年更名为Rethink Robotics)公司成立,并于2011年推出双臂机械臂Baxter,于2014年推出协作机械臂Baxter;2015年Rethink推出第二款单臂协作机械臂Sawyer,比较擅长处理高精度工业任务。
因此,无论是UR还是Rethink,协作机械臂最初诞生的服务对象是中小企业。并自2012年后,四大家族为首的传统工业机械臂企业开始了协作机械臂市场的角逐,KUKA于2013年推出7轴轻型灵敏机械臂LBR iiwa,ABB于2014年发布双臂YuMi和单臂Roberta(2015年收购Gometec),FANUC于2014年推出CR-35iA,Yaskawa于2015年推出Motoman-HC10.
相比国外协作机械臂,国内起步较晚,诞生发展迅速。2014年,在上海分别诞生中科新松、节卡两家公司; 2015年,在北京分别成立遨博、珞石两家公司;2016年,达明公司在台湾成立(内建视觉、智能工厂管理软件以及应用解决方案),艾力特在苏州成立(底层操作系统、硬件软件、工艺包与顶端算力、模组关节技术等自主研发);2017年,大族机械臂在深圳成立,拥有电机、伺服器、运动控制经验;2018年,长广溪在无锡成立,主推车规级高速协作机械臂,是国内唯一一家符合IATF16949:2016国际汽车质量管理标准的公司。
当前国内外协作机械臂厂商及产品汇总如表1
| 厂商名称 | 属地 | 主要产品 | 单臂 | 双臂 |
|---|---|---|---|---|
| Universal Robots | 丹麦 | 双:UR3e、UR5e、UR10e、UR16eUR20、UR30 | √ | √ |
| Rethink Robotics | 美国 | Baxter、Sawyer | √ | √ |
| ABB | 瑞士 | YuMi、Roberta、CRB | √ | √ |
| KUKA | 德国 | LBR iiwa、iisy | √ | |
| Fanuc | 日本 | CR-35iA、CR-4iA、CR-7iA | √ | |
| Yaskawa | 日本 | Motoman-HC10、MotoMINI | √ | |
| Bosch | 德国 | APAS | √ | |
| Franka Emika | 德国 | Franka Emika | √ | |
| 遨博智能 | 北京 | AUBO-i5 | √ | |
| 节卡 | 上海 | JAKA Zu、All-in-one、Pro、C、Mini | √ | |
| 中科新松 | 上海 | GCR30、SCR | √ | |
| 珞石 | 山东 | SR、CR、ER | √ | |
| 大族 | 深圳 | Elfin | √ | |
| 长广溪 | 无锡 | C系列、G系列、X系列 | √ | |
| 达明 | 台湾 | TM5 | √ | |
| 越疆 | 深圳 | DOBOT M1、Nova、CR | √ | |
| 思灵 | 中德 | Diana 7、Thor | √ |
参考文献
[1] “Mechanical Advantage – Two Northwestern University engineers are developing cobots — machines that, unlike robots, cooperate with workers without displacing them”. Chicago Tribune. December 11, 1996.
[2] “Cobots” US Patent 5,952,796, filed 1997
[3] ISO-TS 15066-2016 Robots and robotic devices — Collaborative robots
[4] Taesi C, Aggogeri F, Pellegrini N. COBOT Applications—Recent Advances and Challenges. Robotics. 2023; 12(3):79. https://doi.org/10.3390/robotics12030079
[5]陶波,赵兴炜. 协作机器人[M] 清华大学出版社.2023.12
协作机械臂系列包括协作机械臂的发展概述、构型、结构、运动学、运动规划、视觉、多机协同、ROS操作系统、场景应用、工程实践共十节内容,本篇为第二节:协作机械臂的结构构型。
在市面产品整理时发现,当前市面上协作机械臂有6轴、7轴和欠自由度的,也有双臂和单臂的,还有固定作业和搭载移动底盘的。整体看来,构型变化较多,差异较大。以下分析若存在错误的地方,烦请评论区指点一二。
1 自由度
对于工业机械臂来说,构型相对简单统一,考虑到刚体的3个沿轴平动和3个绕轴转动,机械臂通常由前三个关节确定位置,后三个关节确定姿态,从而实现机械臂末端能够到达工作空间的每一个位置并做出需要的姿态,部分应用场合只需要平面运动或者有限运动,则在6自由度的基础上简化为欠自由度关节驱动以降低成本。
现有协作机械臂相比工业不同的是7自由度的冗余构型。原则上,末端具有6个自由度的关节机械臂再给定的空间可以完成任意位置和任意方向的工作,但实际上由于各关节运动到特殊位置所产生的奇异情况和工作空间内障碍物的存在,机械臂在某些情况下会失去一个或几个自由度,妨碍工作进行,因此提出用冗余自由度避开奇异位置和障碍物,但这也带来难以控制、精度下降等问题。
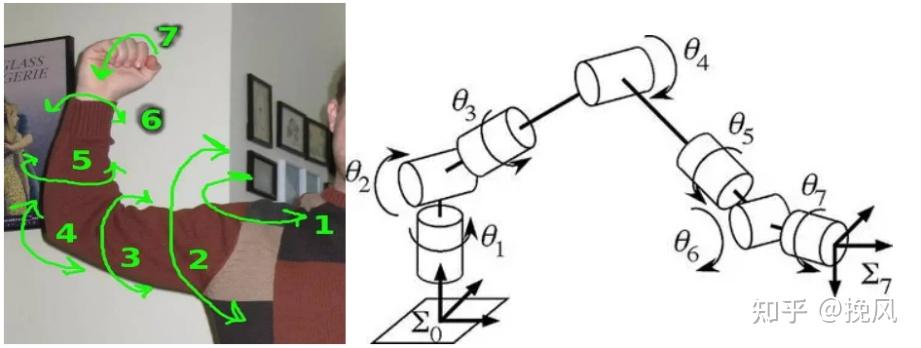
关于7自由度的构型,除了“臂角”增加的设计之外,还源自生物学参考——人的手臂(从肩关节到腕关节)有7个自由度。但是之所以工业机械臂最早的时候未采用7轴,可能主要是因为七轴的运动学解析解的技术问题,其次是成本、市场应用的需要等工程方面的考虑。当然目前求解问题已有解决,最常见的构型是采用前三轴相交于一点,构成第一个球关节,后三轴相交于一点,构成第二个球关节,称为S-R-S结构[1],这种构造比较容易得到运动学求解。
2构型
一般而言,协作机械臂通过关节驱动连杆结构将关节空间映射到笛卡尔空间坐标系,而协作机械臂的构型决定了其空间映射关系。构型设计是机械臂设计的基础和关键,为了方便描述构型设计,下述给出了关节间位置关系及位置关系的编码命名。
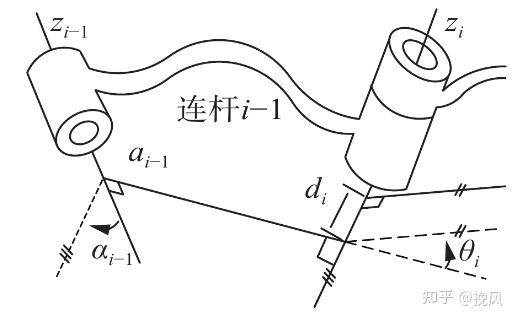
目前市面上常见的协作机械臂均采用转动关节R,连杆中两端关节的位置关系如图2所示[2],其中zi−1、zi 表示相邻关节的轴线, ai−1 表示相邻轴线间的公垂线长度,di表示连杆偏置,θi表示关节的转角, αi−1表示连杆的扭角。
根据图1所示的两关节之间的位置关系,可以借鉴Gogu[3]使用的运动副种类及空间连接位姿的二进制数据表示法。由于D-H参数中4个变量,其中的关节转角θ不影响连杆本体构型参数,故简化使用3位2进制表示相邻关节的位置关系,其中:
第1位表示连杆的扭角αi−1,平行为0,垂直为1;
第2位表示轴线间公垂线长度ai−1,无公垂线为0,有公垂线则为1;
第3位表示连杆偏置di,存在偏置则为1,无偏置则为0。
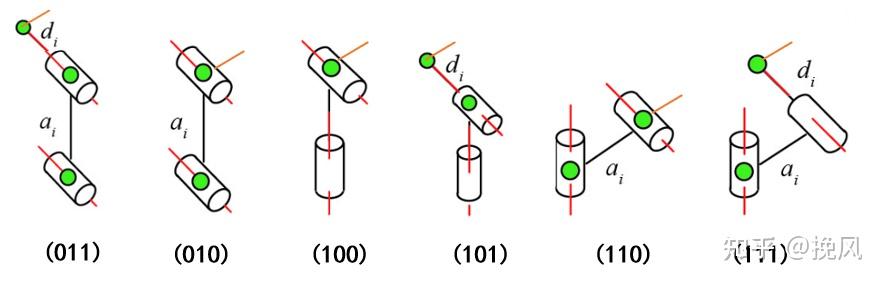
正常来说,该编码可以产生2³=8种组合型式,但结合实际制造情况,应有6种位置关系,如图3所示。其中,011是指关节轴线相互平行,公垂线为平行轴线间的距离,连杆存在偏置;010是指关节轴线相互平行,公垂线为平行轴线间的距离,连杆不存在偏置;100是指关节轴线相互垂直,且轴线相交于一点,无公垂线也无连杆偏置;110是指关节轴线相互垂直,无公垂线,但关节之间存在偏置;101是指关节轴线相互垂直,有公垂线但无偏置;111是指关节轴线相互垂直,有公垂线且有偏置。
当前协作机械臂的关节关系可以看成是上述6种编码的组合关系。以UR机械臂的UR3系列的机械臂为例分析,如图4所示,关节1-2的编码关系是101;关节2-3的编码关系是011,关节3-4的编码关系是011,关节4-5的编码关系是101,关节5-6的编码关系是100。其他类型的协作机械臂可依据此分析。
在决定最佳构型时,采用不同的方法得到的配置不同,归彤等人[5] 将6或7自由度关节分为两部分,靠近基座的前3-4个关节决定末端位置,将腕上的后3个关节决定末端姿态,提出使用位置空间、奇异空间、回避障碍和回避奇异的性能评价机构构型。田勇等人[4]则将偏置对关节运动范围的影响分为S型偏置和Y型偏置,以全局性能指标、工作空间体积指标和灵活工作空间指标为性能评价标准,对比分析说明偏置的存在使构型的全局性能和工作空间体积性能降低,但对灵活工作空间性能有提高作用。还有另一种按照是否满足Paper准则来确认构型(Paper法则的定义是:对于一台6轴机械臂,其逆运动学具有封闭形式解的一个必要条件是3个腕关节的轴相交于一点)。
在构型综合设计过程中考虑的设计要求越多,优化得到的机械臂整体性能就越优越,根据潘新安[6]等人提出的优化构型设计中,需要根据构型对关节角度的限制范围、去除冗余的拓扑结构(不包括设计所需的冗余)、末端可达位姿、零位要求(零位保持直立状态减少重力影响)、运动学逆解或算法的计算程度等综合考虑。
3 现有产品的构型分析
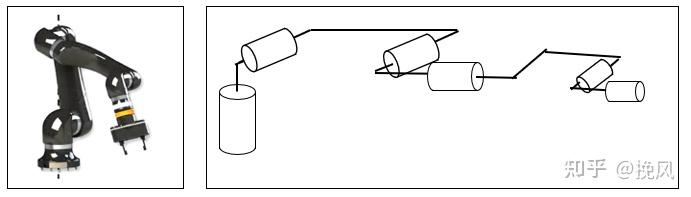
ABB于2015年收购协作机械臂公司Gomtec发布单臂Roberta,该机械臂的结构构型如图5所示,关节1-2编码为101,关节2-3编码为011,关节3-4编码为101,关节4-5编码为101,关节5-6编码为101.该构型为典型的工业机械臂的传统构型。
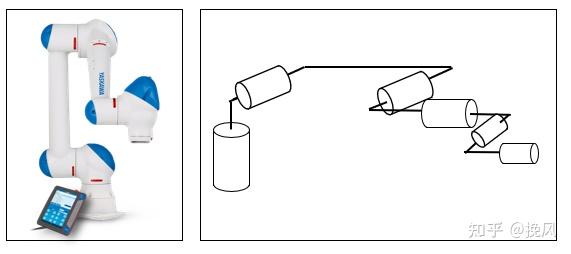
Yaskawa于2015年推出的Motoman-HC10,其构型相比Roberta而言,各关节构型的编码是一致的,但是,可以看到关节4、关节5、关节6的偏置方位不同,Roberta的后三个关节是交于一点的,而HC10的后三个关节则4-5相交,5-6相交,末端轴线偏置在另一侧。
这里需要引入整机构型的分析。对比UR3、Roberta、HC10的三个构型,这是当前六自由度比较常见的三种构型,其主要区别在于后三个关节,比如四轴与关节3平行还是垂直,关节4、5、6是否相交于一点等。三种不同构型分别对关节角度的限制范围、末端可达空间、零位要求(零位保持直立状态减少重力影响)、运动学逆解或算法的计算程度的影响程度不同。
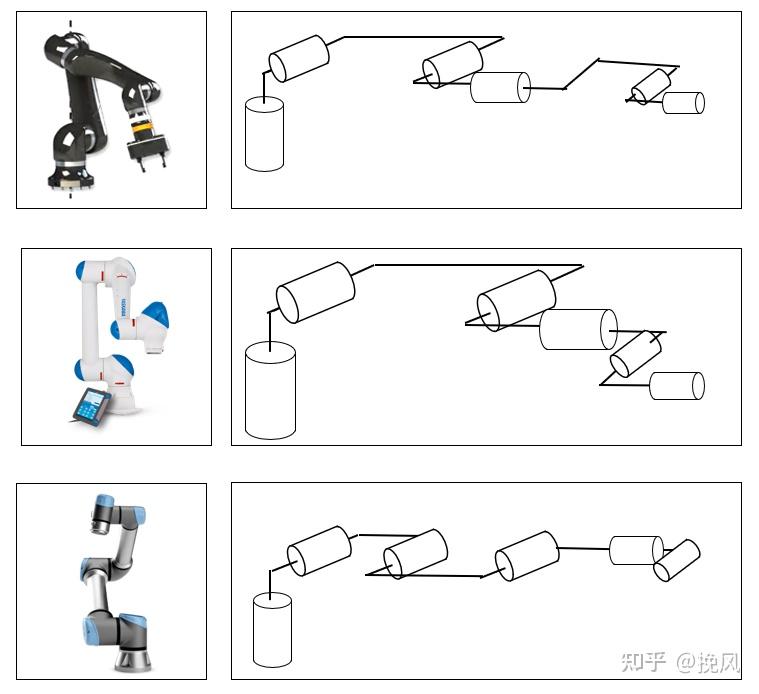
对于七自由度来说,KUKA的iiwa机构构型如图8所示,关节之间全部由100编码的位置关系相互连接,其余构型则在此基础上多了一些偏置。
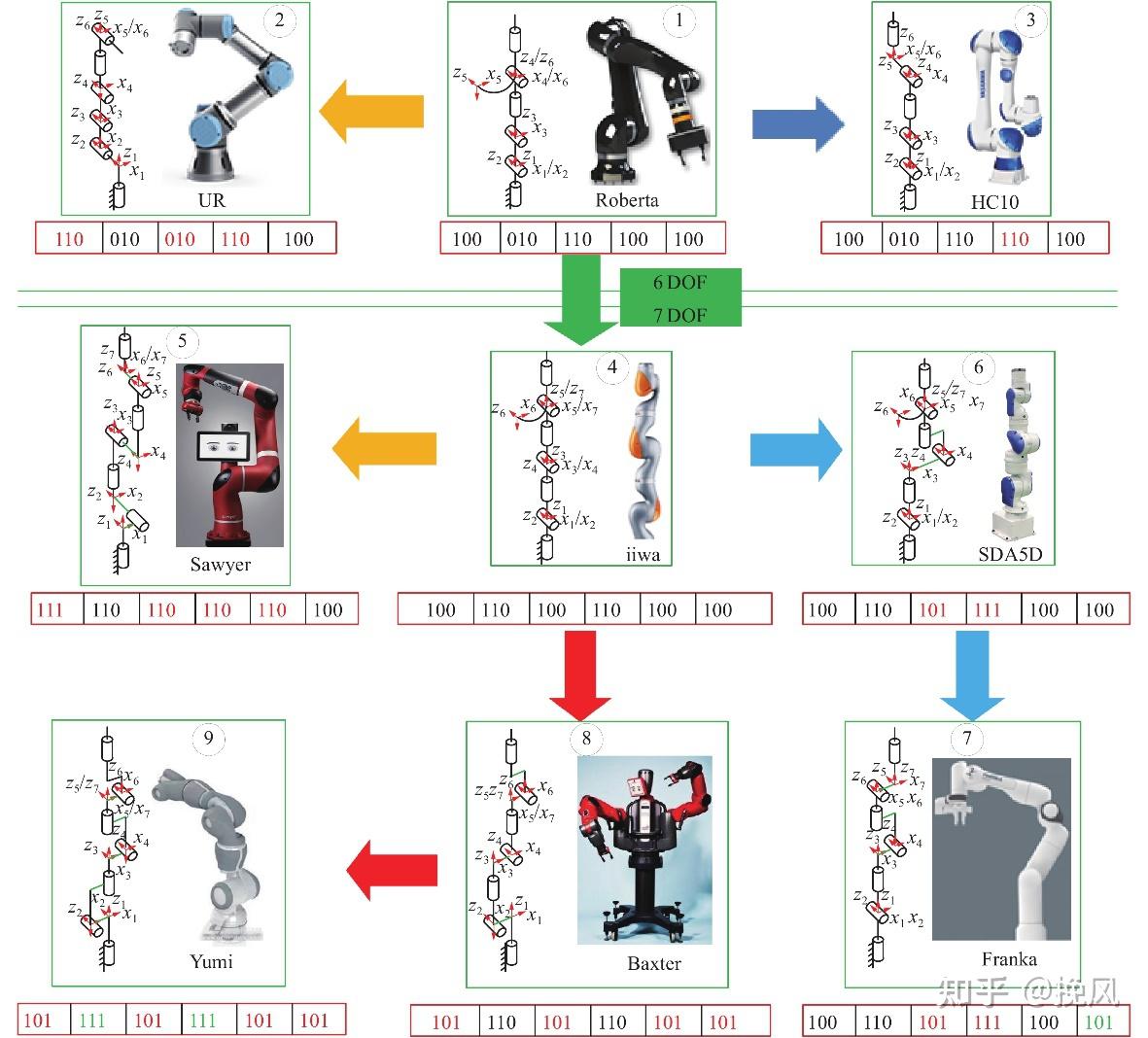
以上仅提出了一些当前的常见构型和构型评价方面,但是至于每种构型的优劣好坏,在这里留个尾巴,让我们放到运动学一节细说。
参考文献
[1] HOLLERBACH J M. Optimum kinematic design for a seven degree of freedom manipulator[C]//Proceedings of the Robotics Research: The Second International Symposium. Cambridge, USA, 1985: 215–222
[2] John Craig. 机器人学导论(原书第4版).
[3] GOGU G. Structural synthesis of fully-isotropic parallel robots with Schönflies motions via theory of linear transformations and evolutionary morphology[J]. European journal of mechanics-A/solids,2007,26(2):242-269. DOI:10.1016/j.euromechsol. 2006.06.001
[4] 田勇, 王洪光, 潘新安, 等. 协作机器人的构型分析研究[J]. 智能系统学报, 2019, 14(2): 217-223. DOI: 10.11992/tis.201806044
[5] 归彤, 原培章. 7自由度机器人的图谱问题[J]. 机器人, 1991, 13(4): 27-30.
[6] 潘新安, 王洪光, 姜勇, 李正, 高文斌. 一种模块化可重构机器人系统的研制. 智能系统学报[J]. 2013, 8(4): 292-298.
协作机械臂系列包括协作机械臂的发展概述、构型、结构、运动学、运动规划、视觉、多机协同、ROS操作系统、场景应用、工程实践共十节内容,本篇为第三节:协作机械臂的结构。
协作机械臂的结构篇重点关注以下几个方面:一体化关节构成组件、抱闸设计、力感知设计、连杆外壳设计等。
1 一体化关节
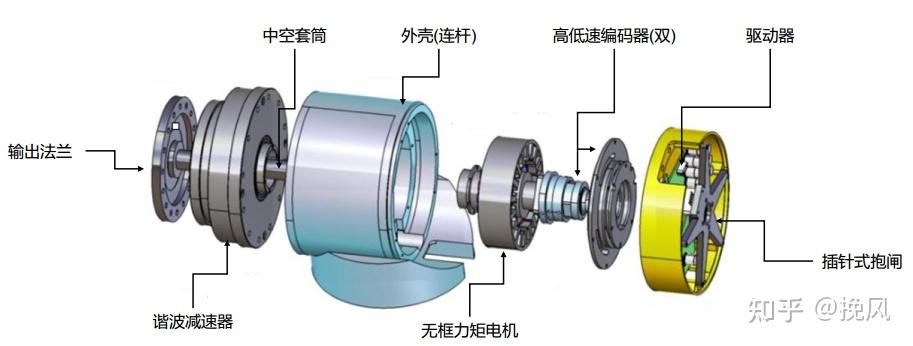
协作机械臂区别于工业机械臂的结构特点,在于高度机电系统集成的一体化关节,当前大致可分为类UR关节、类iiwa关节、类Sawyer关节和模组公司关节四类。
类UR关节是采用UR关节的构造,其主要构成部分如图1所示,从左到右依次是输出法兰,高精密谐波减速器、中空线束套筒、连杆(无框电机外壳)、无框力矩电机、高低速端双编码器、传动轴、驱动器、插针式抱闸。
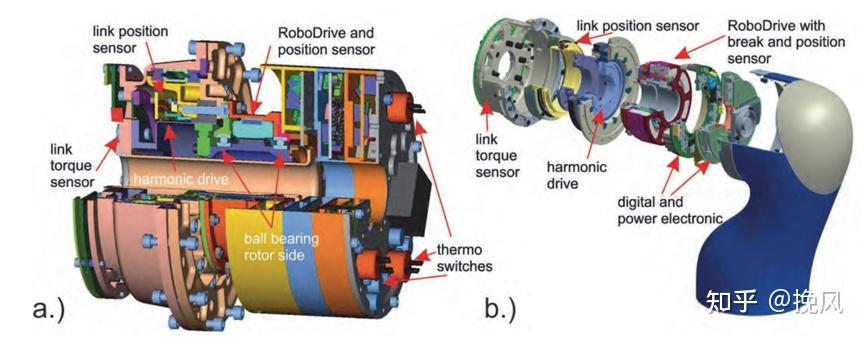
类iiwa关节的主要构成部分如图2所示,该结构为德国宇航中心基于第3代轻型臂开发的模块化双关节机器人ROKVISS关节内部构造,从左到右依次是连杆扭矩传感器(link torque sencor)、输出端编码器(link position sensor)、谐波减速器(Harmonic drive)、包含抱闸和编码器的无框力矩电机模块(RobotDrive with brake and position sensor)、驱控板(digital and power electronic)、风扇(散热用的)、最后是连杆、外壳,采用中心孔走线,实时串行通讯的总线结构,具有丰富感知能力,包括位置感知、力矩感知、温度感知以及电流感知。
类Sawyer关节的主要构成部分如图3所示,相对于前两个关节,其主要特点是谐波减速器上弹性体编码器,通过测量两个端面的偏角再乘以抗扭截面系数得到关节力矩,这个偏角是通过磁环+编码器的方式获得。
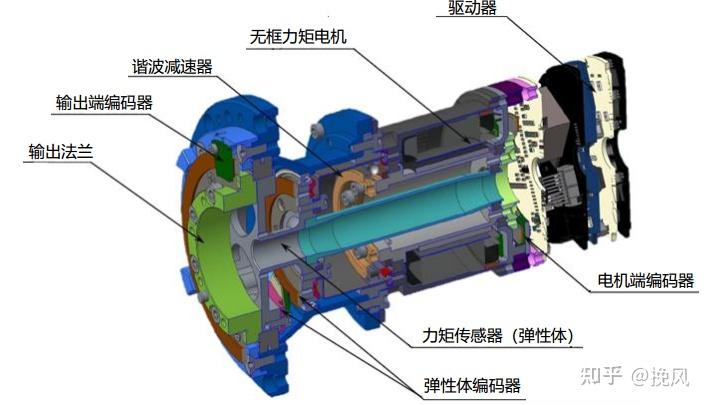
模组公司关节则指当前单独做机器人模块关节的公司,其产品结构特点均以无框力矩电机、谐波减速器、编码器、驱控电路、抱闸等为基本组件,比如科尔摩根(KOLLMORGEN)的RGM关节,如图4所示,由无框力矩电机、低压直流驱动器(48VDC供电)、定制谐波减速器、双反馈系统(采用19位单圈绝对值编码器)、双热敏传感器和制动器组成。这类模组可能与机器人整机厂商会略有不同,但大致结构都是相同的。

由上分析,虽然协作关节的结构都很类似,但是我会比较好奇关节的一些细节点:
(1)编码器的选配使用
(2)抱闸的选配使用
(3)电机、减速器的型号配置
(4)力感知功能的方案
2 编码器
2.1 编码器基础
我对编码器的了解很少,特意花了大篇幅来学习编码器。
编码器是读取特定编码的传感器设备,常用于闭环控制应用中测试旋转、线性运动的精准位移。编码器在储存编码时,需要编码与物理位置严格一一对应,其编码介质可以是玻璃、金属、磁铁,等生产后一般是不可更变的。
按照原理不同,编码器有光电编码器(编码线刻在动件上,改变刻线的透光性进行0、1编码)、电容/电感/旋变编码器(动静件的电磁转化来测量位置)、磁编码器(磁铁的NS极以特殊图案磁化在磁铁上,读取磁场强度确定位置),这三类光电编码器精度最高。
按照输出不同,编码器又分为绝对值编码器(发出数字信号,又数据格式规定,需要上位机通信)和增量编码器(模拟信号,下位机通过模数转换获取位置),绝对值编码器分为单圈(可探知360°内绝对角度)、多圈(除了探知360°角度,还可记录当前的圈数);增量编码器分为方波(输出为相位差90°的方波)、弦波(输出为相位差90°的弦波)
2.2 磁编码器原理与方案
谐波关节中常用磁编,故特别学习一下磁编的原理。
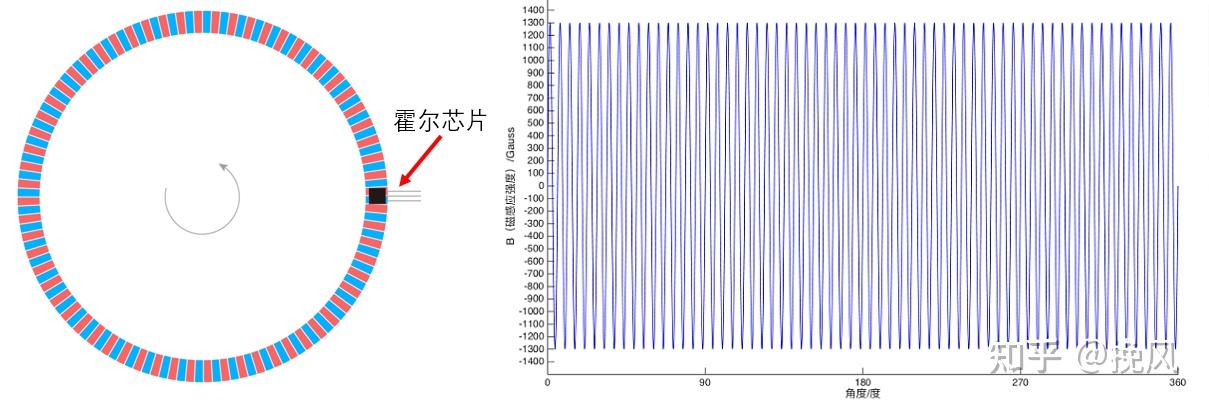
磁编的动件磁性物质,其载体是铁氧体、钕铁硼、钐钴等磁性材料。多极磁编的磁环图案为下图。

该磁环的工作原理为:128极(64对NS极)平面充磁后,会产生64个弦波周期,磁场方向为垂直纸面,线性霍尔芯片放在磁环平面(此处元件可以是霍尔芯片,根据霍尔原理感应电压,也可以是磁阻感应元件,感应磁场变化),当磁环旋转时,霍尔得到以下波形,但旋转一周只能得到相应的角度变化(增量),无法得到具体位置。
为了得到具体位置(绝对角度),则需改进编码器原理,主要有单对极磁铁(相差90度各放置霍尔芯片,按照正交波形求解唯一对应值)、磁游标(两条磁码值,外圈32对,内圈31对,每一个位置内外圈磁感应强度不同)、磁刻线(分为很多细线,细线宽度不同)。

- 当需要绝对定位高精度(16bit以上)时,您可选择磁游标或磁刻线方案
- 需要绝对定位且于恶劣、复杂的工况下,选用单对极方案
- 需要增量且精度极高时,选用多对极方案
- 需要增量于普通工况时,选用单对极方案
2.3 编码器的精度
作为角度测量传感器,测量精度是最为关注的,编码器的测量精度常用“绝对定位精度”和“重复定位精度”,该精度受位置、环境的影响。其中,位置是指编码器测量中测量装置(静件)和被测量装置(动件)之间的安装误差;环境则是指温度、灰尘、湿度、液体、磁干扰(磁编码器较为敏感,会与磁环的磁场叠加,因此常需要磁屏蔽罩)
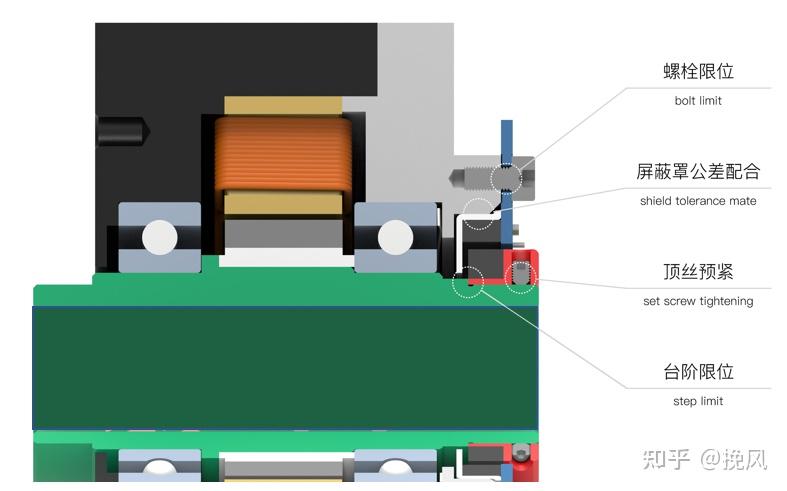
磁编的动件会固定在被测量轴上,静件固定在壳体上,固定后确定编码器的动静件相对位置:编码器本体使用PCB上的安装孔固定,磁环使用顶丝预紧固定,且安装顺序为:先安装编码器本体,后安装磁环。编码器本体使用本体上的屏蔽罩与电机的壳体进行配合,使用屏蔽罩与壳体的高精度尺寸公差进行间隙配合,最大程度地将编码器与壳体的中心位置对齐,从而与轴以及要安装在轴上的磁环减小同心度误差。磁环使用轴上的轴肩进行限位,该限位应使磁环与编码器本体的轴向相对位置与标定时的相同。
2.4 协作机械臂编码器
市面上常见的协作机械臂似乎都是双编,常见的结构如图10所示,通过中空轴设计,将输出轴的编码器转移至电机定子侧,而输出轴反向多一个穿过中空轴的回路轴,为编码器提供数据,避免编码器定子固定与走线问题。
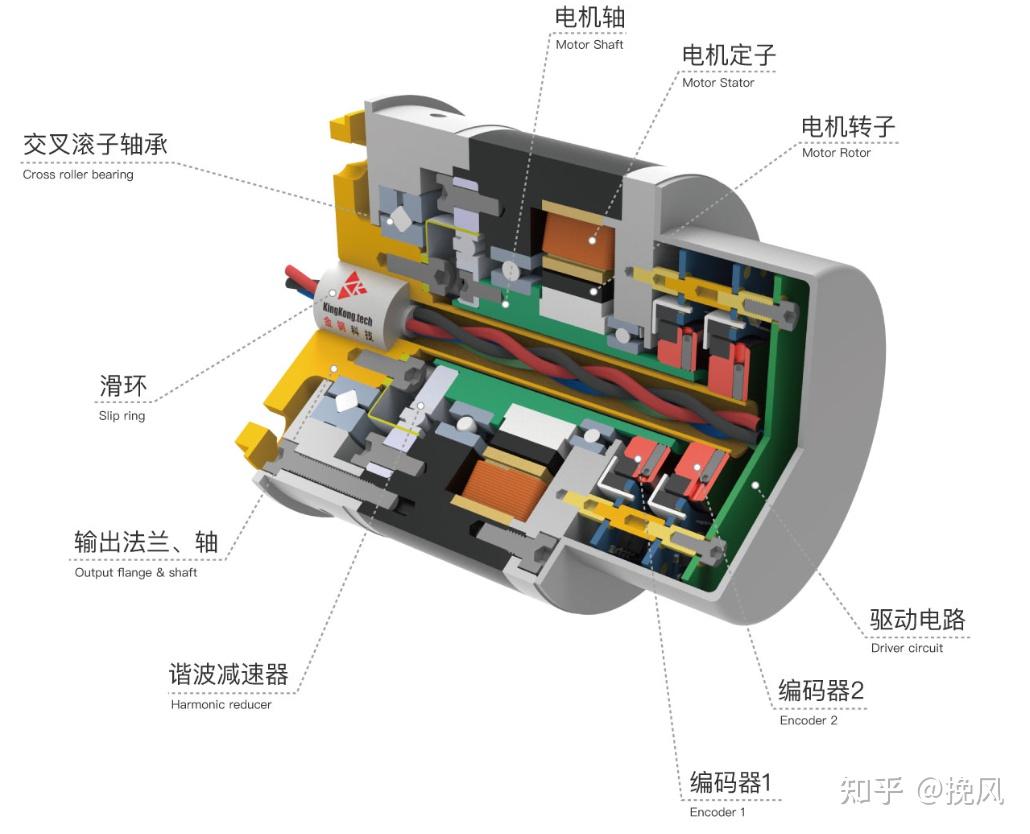
静态时,输出侧受到外部扭矩,输出侧编码器测量到微小变化,但电机侧编码器由于减速比的存在未能及时感知到,通过两者对照可得到外力扭矩的微小变化,驱动器开启算法——若是拖动示教,则电机跟随受力;如果仅是静态负载扭矩,电机补偿外部受力以保持位置稳定。
动态时,电机侧输出数据,通过计算得到输出端的理论位置,再与输出端的实际反馈值进行对比,得到外力大小,反馈给驱动器进行后续控制。
在选用编码器时,电机侧编码器反馈的数据主要用于PID、FOC控制,其精度的选择需要和减速后输出侧的精度相适配,而不是追求高分辨率;输出侧是用于直接测量输出位置的变化,其分辨率需要匹配测量扭矩的范围(因为主要测量外界微小力的变化,故而需要追求分辨率,而不是追求绝对定位精度)
3 力感知设计
在建立人机协作工作之前,安全是需要解决的首要问题,安全性体现在碰撞检测和低压伺服关节两方面。
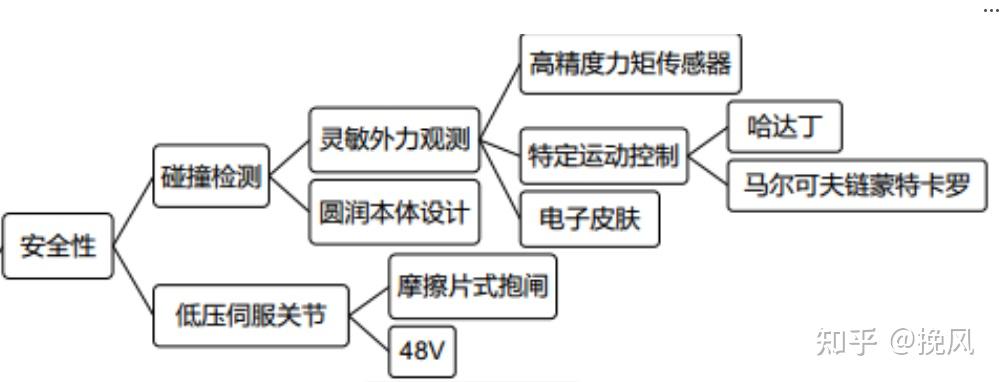
对于碰撞检测的安全性,最容易考虑到的是在机器人身体上使用粘弹性覆盖物来减少冲击力[5]。一般来说,机器人本质上危险的是高速度和巨大的移动惯性的结合,被动顺应冲击的方案使得协作机械臂可以安全运行而不限制所需动态性能,串联弹性制动器和串并联弹性制动器被提出来,算是一种机械解决方案吧,使用的是可变阻抗驱动(variable impedance actuation,VIA)。而在VIA中,最先被研究出来的是使用可变刚度执行器(Variable stiffness actuators,VSA)为机器人提供内在的顺应性,VSA本质上是机械致动系统,将负载扭矩施加到输出轴时,允许输出轴从平衡位置产生位移。在静止状态下,该位移通过机械刚度特性与所施加的扭矩相关。
除了采用机械缓冲之外,另一种方式是通过扭矩感知的方式,现有一下方案:
(1)电流:通过电机线圈的电流估算外力,方便但精度低
(2)双编码器:加装高分辨率编码器以测量输出端位置变化计算扭矩,费用低,精度高
(3)扭矩传感器:在输出端加装扭矩传感器测量,费用高,算法难度高;
(4)应变片:在谐波柔轮上装贴多组应变片以测量扭矩,结构极其复杂,标定难度高。
机械缓冲+扭矩感知的结合体应当算是人造皮肤了。Fritzsche[6]为机器人身体提供用作人造皮肤(pressure sensitive skin)的触觉传感器(Tactile sensing)来监测接触力。但是为了减少危险伤害的风险,这种人造皮肤不仅仅能够监测接触力,同时还需要保有一定的减震缓冲作用(减少撞击对人体以及对传感器的损坏程度),Staubli和越疆的协作产品似乎都在采用电子皮肤。
4 电机、减速器
4.1 无框力矩电机
无框力矩电机保留了传统电机用于产生扭矩和速度的部分(只有定子、转子),而去除了轴、轴承、外壳或端盖,是以输出扭矩为衡量指标的无框架式永磁电机,由驱动器控制U/V/W三相电形成电磁场,永磁体转子在磁场作用下转动。相比之下,普通伺服电机偏向于以输出功率为评价指标,而无框力矩电机更偏向于以输出扭矩为衡量指标。

无框力矩电机可以通过霍尔元件作为反馈信号,也可以通过另外加装的编码器信号作为反馈。驱动器根据反馈值和目标值进行比较,调整转子转动角度,从而达到伺服驱动的目的。
4.1.2 选型
协作机械臂所用无框力矩电机,所关注的参数有两个方面,一方面是机械设计参数,另一方面是伺服驱动参数。
(1)机械设计参数
机械设计参数最先关注的是力矩、转速、惯量性能。协作机械臂在电机选型时,需要的扭矩越大,定子叠厚或定子外径就会越大;转速与输入电压/电磁方案有关。考虑到协作关节多采用大尺寸中空直径和低重量高功率密度的设计,以实现自重轻、中控走线、结构小巧灵活的特点。此外,还需要考虑现有谐波减速器产品的适配情况。
(2)伺服驱动参数
电机的额定电压、反电动势、功率因数、最大电流等
4.1.3 霍尔传感器
霍尔元件是一种基于霍尔效应的磁传感器,如图,在一块通电的半导体薄片上,施加垂直于薄片的磁场B,在薄片两侧会出现霍尔电压VH
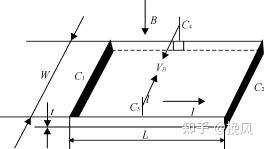
霍尔开关电路由稳压器、霍尔片、差分放大器、斯密特触发器和输出级组成,在外磁场作用下,当磁感应强度超过导通阈值时,霍尔电路输出管导通,输出低电平,此处导通阈值BOP称为工作点。若外加磁场的B值降低到BRP时,输出管截止,输出高电平,BRP为释放点。BOP-BRP=BH称为回差,回差的存在让开关电路的抗干扰能力增强。
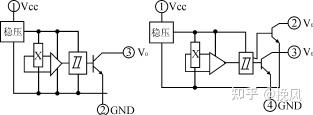
在电机定子的适当位置放置所需数量的霍尔器件,他们的输出和相应的定子绕组的供电电路相连,当转子经过霍尔器件附近时,永磁转子的磁场令已通电的霍尔器件输出一个电压使得定子绕组供电电路导通,给相应的定子绕组供电,产生和转子磁场极性相同的磁场,推动转子继续转动。到了下一个位置,前一位置的霍尔器件停止工作,下一个霍尔器件通电,使得下一绕组通电,如此循环维持电机的工作。
此处,霍尔元件起位置传感器的作用,检测转子磁极的位置,然后输出霍尔电压使定子绕组供电电路通断;霍尔元件又起到开关作用,当转子磁极离开时,令上一个霍尔器件停止工作,下一个器件开始工作。
4.1.4 安装
无框电机组件利用配合公差和现有的工业粘合剂安装到基本的机器外壳中

4.2 谐波减速器
谐波部分被我做进MST工具集了,就不在此记录了。

5 抱闸设计
抱闸(又称制动器)是用于机械臂静态时固定机械臂关节负载,而非用于主动刹车制动,抱闸属于刹车中的一部分,但还存在其他电气/机械刹车方法。
顾名思义,抱闸就是“断电抱死电机轴,通电松开电机轴”的制动器,现阶段协作机械臂的制动抱闸主要有两种:一种是电磁插销式抱闸,一种是电磁摩擦片式抱闸。
5.1 电磁插销式抱闸
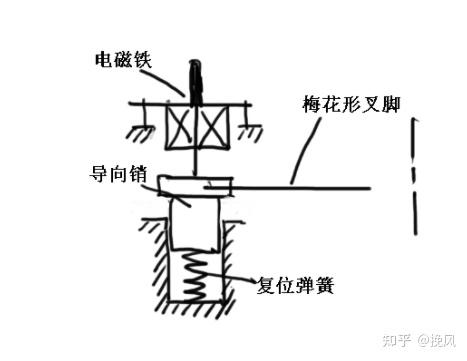
电磁插销式抱闸由电磁铁、复位弹簧、梅花形叉脚、导向销等组成;梅花形叉脚与电机轴直连,在电磁铁未通电的状态下,导向销在复位弹簧作用下弹起,其肩部刚好可以挡住梅花形叉脚,这是抱闸处于闭合状态;

在电磁铁通电或手动按下状态下,导向销下沉,其肩部低于梅花形叉脚,这是抱闸处于打开状态;方案轴向尺寸更紧凑、电磁线圈发热更小。但是抱闸效果不太好,有一个小的活动范围(电机端6分度 360/6=60°,则该抱闸可移动空间为60/减速比)。此外,机械臂在启动的时候,容易出现制动器解不开的可能,需要控制机械臂反向旋转一定角度后才能松开制动器。
5.2 电磁摩擦片抱闸
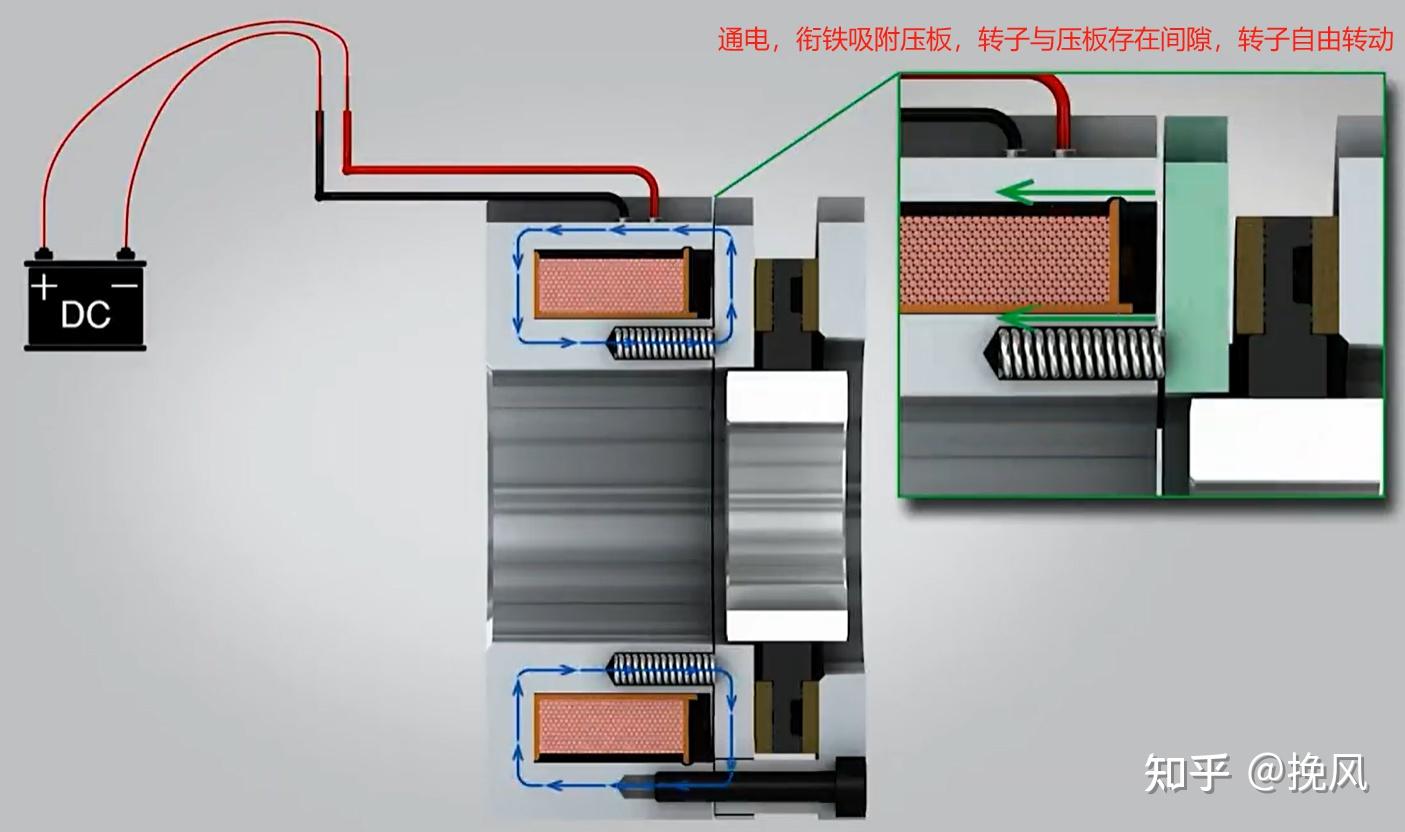
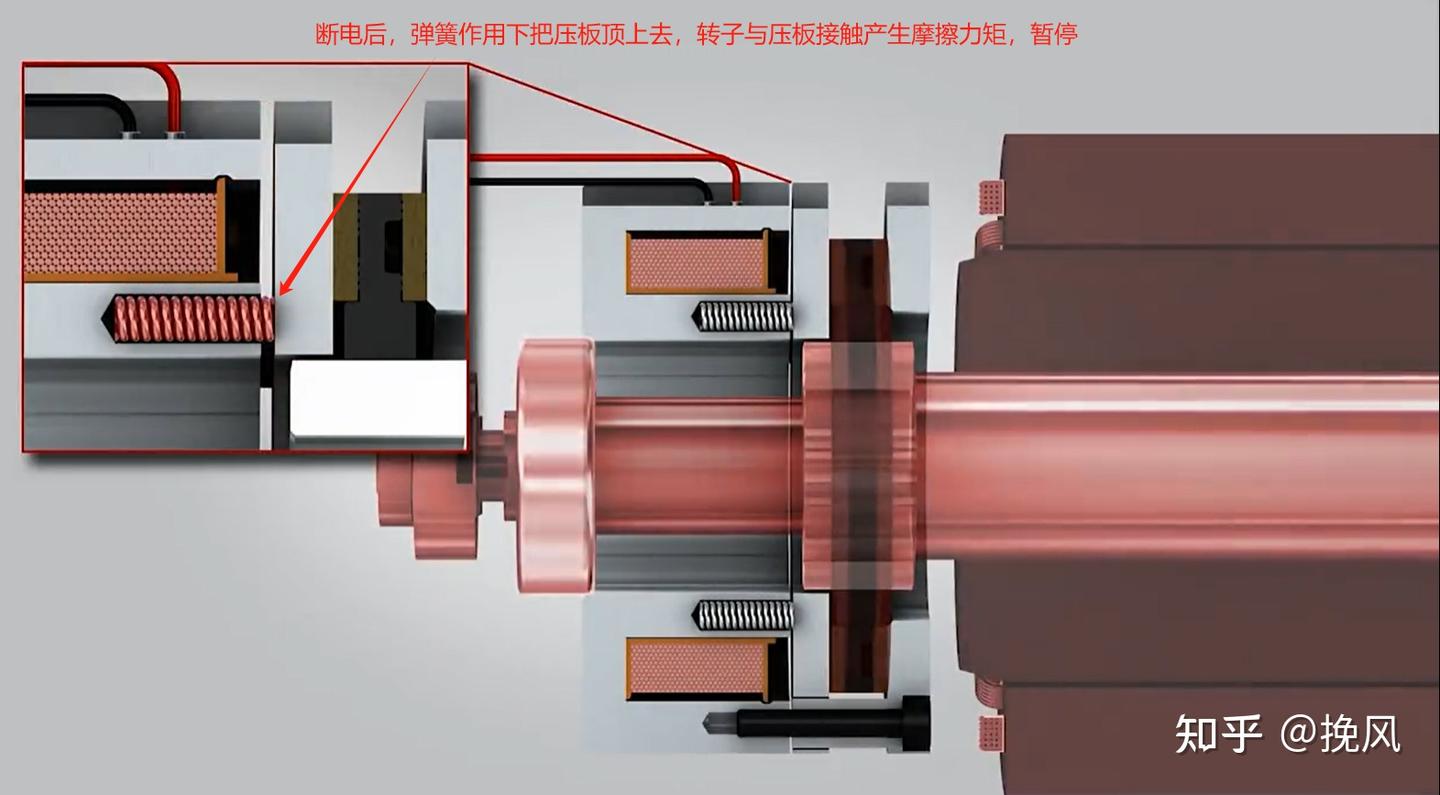
Lenze公司在上世纪推出一款干式双面失电动作型弹簧加压电磁安全制动器[1],结构主要由定子和转子组成,钉子里面是绕线圈,环氧灌封处理;转子是用特定耐摩擦材料制作而成。转子和定子之间通过弹簧加压,使衔铁和平板夹住转子,产生摩擦转矩。

不通电的时候,由于扭矩弹簧的作用,衔铁压住转子,通过所产生的摩擦力对轴伺服电机轴进行制动和保持;当线圈通电时,衔铁在电磁力作用下压缩弹簧,转子被释放,可以自由旋转。
5.3 选型设计
在进行抱闸选型时,一般来说,经验上会提到抱闸力矩约为电机额定力矩的1.3~1.5倍
������=1.5�����������
但是实际上制动力矩并不完全参考电机的额定扭矩,而是令其最大值和最小值满足一定的条件。
最大值:制动力矩必须低于减速器的启停扭矩,否则急停断电的时候制动扭矩过大会造成减速器损坏或者关节偏移,因此其高值不能大于减速器启停扭矩。
最小值:制动时需要具备断电保持姿态的能力,则制动扭矩必须大于负载扭矩(包括末端负载和自重负载),因此其低值不能小于负载转矩。
6 连杆外壳设计
6.1 关节与连杆之间的连接关系
UR的关节与连杆之间的固定方式,据说迭代了三代:
初代:周向螺钉——螺钉头与外壳之间的摩擦力承受应力

次生代:葫芦孔(或者钥匙孔)——生产维护太麻烦

当前:C形卡箍+锯齿+定位Dot,只需要拧进C型卡箍的螺钉即可。


6.2 连杆材质和制造加工
对于直筒管式的连杆,成型工艺可能是铝管挤压成型,然后两端法兰摩擦焊。

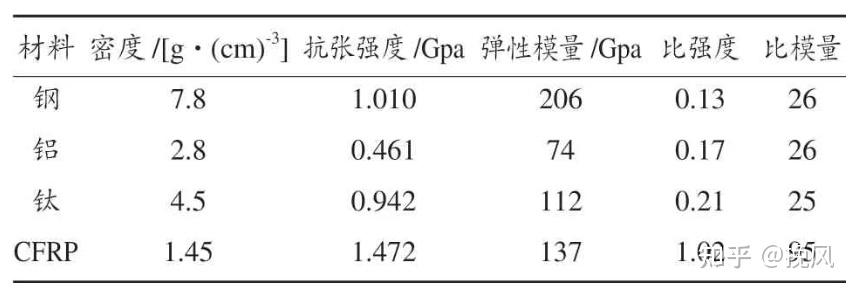
对于复杂曲面成型,大概率就是3D打印和铸造加工了,我比较关注的是当前复合材料的机械臂成型工艺。目前,机器人制造的主要材料还是高强度钢和铝合金材质,碳纤维、镁铝合金及其他复合材料的应用均受限于应用成本和技术水平。目前市面上已经开始出现了机器人外壳、臂管等机械臂本体结构零部件碳纤维制品,这些类材料多为热固性碳纤维复合材料,整体还需进一步发展连续碳纤维增强热塑性复合材料。
碳纤维复合材料的密度为1.6g/cm³,更加轻量化;碳纤维机械臂具有非常高的抗拉强度(达到3500MPa),且抗疲劳性跟高,蠕变小、热膨胀系数低、不容易发生变形弯曲,对比如下。
碳纤维机械手臂采用的制作工艺是模压成型工艺,需要先根据设计模型——设计生产模具——根据机械臂尺寸进行碳纤维预浸料裁剪——根据机械臂力学性能要求进行铺层设计。
但目前还没有减到市场大规模换用碳纤维材质,原因可能在于气密性、铺层设计、模压参数等生产工艺经验不充足,待我调研一段期间再补充这方面的内容。
参考资料
[1] 协作机械臂的设计解析及应用介绍 | 珞石机器人研发中心系统工程师任赜宇
[2] G. Hirzinger. N. Sporer. A. Albu-Schaffer. et al. DLR’s torque-controlled light weight robot II –Are we reaching the technological limits now
[3]编码器基础与种类[OL] 金钢科技网
[4] 雷赛对永磁式制动器和电励磁型制动器概述.[J]伺服与运动控制.2017.06
[5] Park, J.J.; Haddadin, S.; Song, J.B.; Albu-Schäffer, A. Designing optimally safe robot surface properties for minimizing the stress characteristics of human-robot collisions. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 5413–5420.
[6] Bicchi, A.; Tonietti, G.; Bavaro, M.; Piccigallo, M. Variable stiffness actuators for fast and safe motion control. Robot. Res.2005, 527–536
[7] Fritzsche, M.; Elkmann, N.; Schulenburg, E. Tactile sensing: A key technology for safe physical human robot interaction. In Proceedings of the 6th International Conference on Human-Robot Interaction (HRI’11), Lausanne, Switzerland, 6–9 March 2011; ACM: New York, NY, USA, 2011; pp. 139–140
协作机械臂系列包括协作机械臂的发展概述、构型、结构、运动学、运动规划、视觉、多机协同、ROS操作系统、场景应用、工程实践共十节内容,本篇为第四节:协作机械臂的运动学。
运动学部分主要包含以下几个内容:
(1)空间描述:给定一个机器人,如果数学描述连杆关系;给定连杆关系描述,如何建模机器人;
(2)位姿变换:同一位姿在不同坐标系中的表达与转换,用变换矩阵表达,在MATLAB中完成坐标转换;
(3)运动学位置描述:由关节空间转换到末端轨迹,或由末端轨迹转换到关节空间的运动学方程;
(4)运动学速度描述:
(5)运动学加速度描述:
(6)运动学机械机构描述:工件、工作台、连杆质心、负载等运动位置、速度、加速度描述
(7)运动学驱动描述:驱动空间与关节空间的转换
1 空间描述
机械臂通过各个轴关节传动使零件或工具在空间中运动,这就需要对各轴关节、工具、空间位置和姿态等进行数学量描述。数学量的描述包括坐标系的表达规则和基于该规则下位姿的参量描述。
1.1 坐标系表达规则
设定一个笛卡尔坐标系规则下的世界坐标系,所以定义的位姿都是参照世界坐标系定义。
因为要描述的对象有多个,就需要在世界坐标系中相应的定义许多坐标系,其中对于机械臂本身来说,坐标系主要描述连杆。
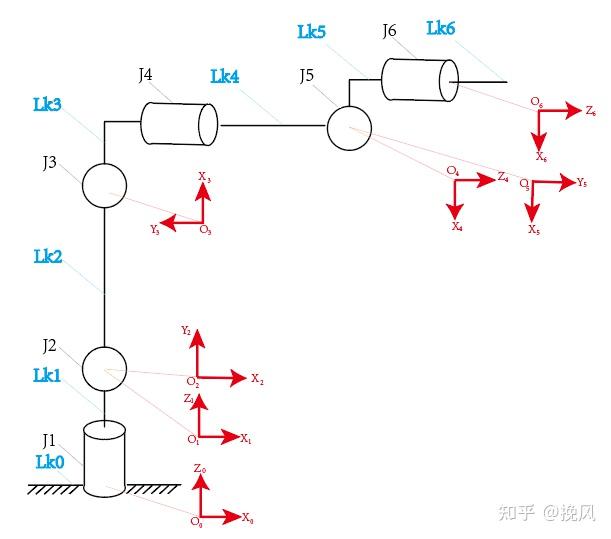
(1)坐标系编号
从机械臂的固定基座开始给各个连杆进行编号,固定基座为连杆0,记作Lk1;第一个可动连杆为连杆1,基座Lk1;依次类推,连杆编号为Lki(i=0~n);相对应的,连杆0上固连坐标系为坐标系0,依次类推。
同样的,连杆0与连杆1的相对转动是围绕关节1来进行的,关节编号为J1,关节的编号与下一个连杆编号相同。
(2)坐标系位置描述
坐标系的位置是固定在机械臂的每个连杆上的,在机器人学中有SDH和MDH两种区分,在SDH中坐标系Z1在关节2的旋转方向上;MDH中坐标系Z1为关节1的旋转方向上。
两平行关节,公垂线与Z1的交点为坐标原点;两垂直关节,交点为原点,都交在关节i上。
(3)坐标系姿态描述
为了研究方便,通常将Z轴设定为转动轴向,以逆时针为正方向时,则以右手法则大拇指朝向为Z轴正方向;
X轴为两Z轴的公垂线方向,但若两关节Z轴相交,X轴垂直于两Z轴所形成的平面;
(4)D-H参数
连杆参数:连杆偏角α(绕X轴转Z轴的角度)、连杆长度a(沿X轴Z方向移动距离)
关节参数:关节转角θ(绕Z轴转x轴的角度)、关节偏距d(沿Z轴X方向移动距离)
DH表:由于SDH的连杆坐标系固定在连杆的末端(下一个关节),而MDH的连杆坐标系固定在连杆的初端(上一个关节),因此表头上能够区分SDH为连杆i,MDH为连杆i-1,区分建议看
@country 写的这篇,很容易看懂。
country:关于DH表的一些实用心得65 赞同 · 4 评论文章
(5)建系步骤总结
对于一个新机构,按照下述步骤正确建立连杆坐标系
- 绘制机构简图:使用轴测图绘制,关节用圆柱体表达,连杆用直线表达(各关节轴的偏置也要绘出)
- 编号:对连杆从基座开始编号Lk0,依次编号至末端执行机构;对关节编号,基座与连杆1所连关节为编号J1,依次编号至末端关节(各编号增加字母或者汉字标识,以区分编号属性防止混乱)
- 建系:选用SDH方式建系,先固定基坐标系(只绘制OXZ),连杆i坐标系固定在关节i+1上,依次类推,末端连杆坐标系;(若采用MDH,连杆i坐标系固定在关节i上),Z轴为转轴方向,逆时针为正方向;X轴指向下一关节方向(Y轴由右手定则确定,不绘出)
- 特别的,基坐标系0位置通常放在基座的安装面上。
1.2 示例
回到协作机械臂系列(二),文末留了一个尾巴,里面罗列了3种六自由度的整机构型和6种七自由度的整机构型,本节示例将按照六自由度的最佳构型与七自由度的经典构型为示例分析,其余构型只展示结果,通过MATLAB程序可自行推敲。
- 六自由度最佳构型示例
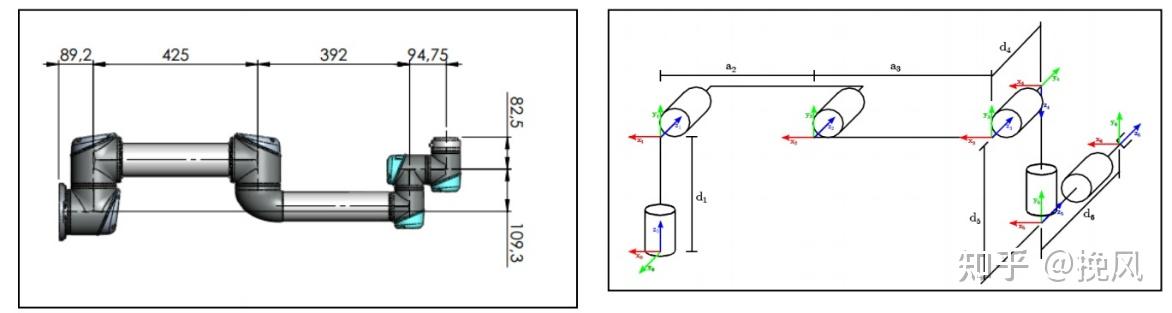
以ABB的Gofa5 CRB15000为例分析,查看《CRB 15000-产品手册》,得到信息如图:
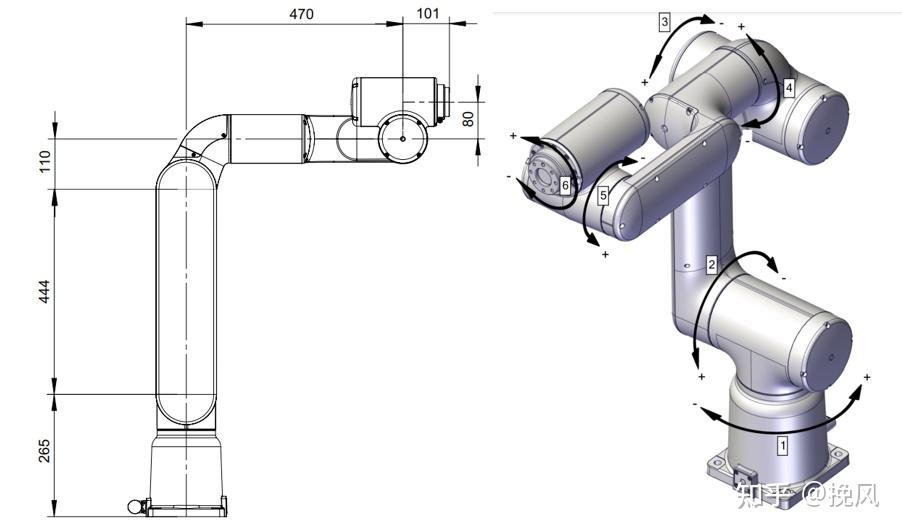
由建系步骤,可绘制机构简图、编号、建系如图2所示(MDH)。
MDH参数如下:
| a | α | d | θ | |
|---|---|---|---|---|
| 1 | 0 | 0 | 265 | θ1 |
| 2 | 0 | 90° | 0 | θ2 |
| 3 | 444 | 0 | 0 | θ3 |
| 4 | 110 | 90° | 470 | θ4 |
| 5 | 0 | 90° | 0 | θ5 |
| 6 | 80 | -90° | 101 | θ6 |
根据MDH表在MATLAB中建模
%%建立协作机械臂模型
% MDH参数
clc,clear
a=[0,0,444,110,0,80];
alpha=[0,pi/2,0,pi/2,pi/2,-pi/2];
d=[265,0,0,470,0,101];
for i=1:6
L(i)=Link([0,d(i),a(i),alpha(i)],'modified');
end
%连接连杆,机械臂取名
Robot_1=SerialLink(L,'name','雎鸠');
Robot_1.base=transl([0 0 0]);
Robot_1.plot([0,pi/2,0,0,0,0]);
Robot_1.display();
关于MDH和SDH建模的区别,感谢
@SAMBELL 的耐心推导,直接贴过来!
SAMBELL:机器人的运动学建模问题及思考(一)33 赞同 · 3 评论文章
- 七自由度经典构型示例
以KUKA的iiwa7为例,查看官网《Kuka_lbr_iiwa_brochure_en》手册,获取信息如图:

由建系步骤,可绘制机构简图、编号、建系如图4所示(MDH)。
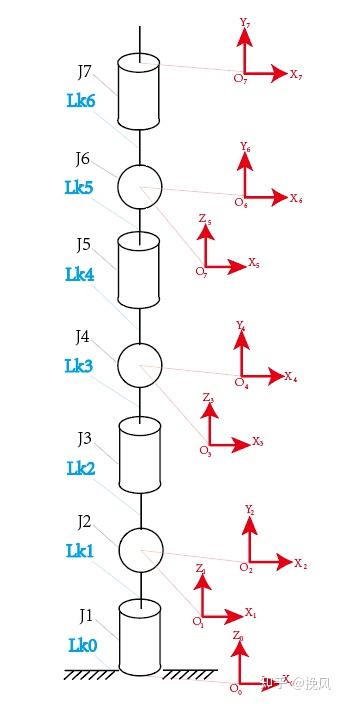
为了便于获取参数,将0、1坐标系原点重合,2、3坐标系原点重合,4、5坐标系原点重合,6、7坐标系原点重合
| a | α | d | θ | |
|---|---|---|---|---|
| 1 | 0 | 0 | 375 | θ1 |
| 2 | 0 | 90° | 0 | θ2 |
| 3 | 0 | -90° | 400 | θ3 |
| 4 | 0 | 90° | 0 | θ4 |
| 5 | 0 | -90° | 400 | θ5 |
| 6 | 0 | 90° | 0 | θ6 |
| 7 | 0 | -90° | 126 | θ7 |
用MATLAB建模
%%建立协作机械臂模型
% MDH参数
clc,clear
a=[0,0,0,0,0,0,0];
alpha=[0,pi/2,-pi/2,pi/2,-pi/2,pi/2,-pi/2];
d=[375,0,400,0,400,0,126];
for i=1:7
L(i)=Link([0,d(i),a(i),alpha(i)],'modified');
end
%连接连杆,机械臂取名
Robot_1=SerialLink(L,'name','JUJIU');
Robot_1.base=transl([0 0 0]);
Robot_1.plot([0,0,0,0,0,0,0]);
Robot_1.display();
Robot_1.teach();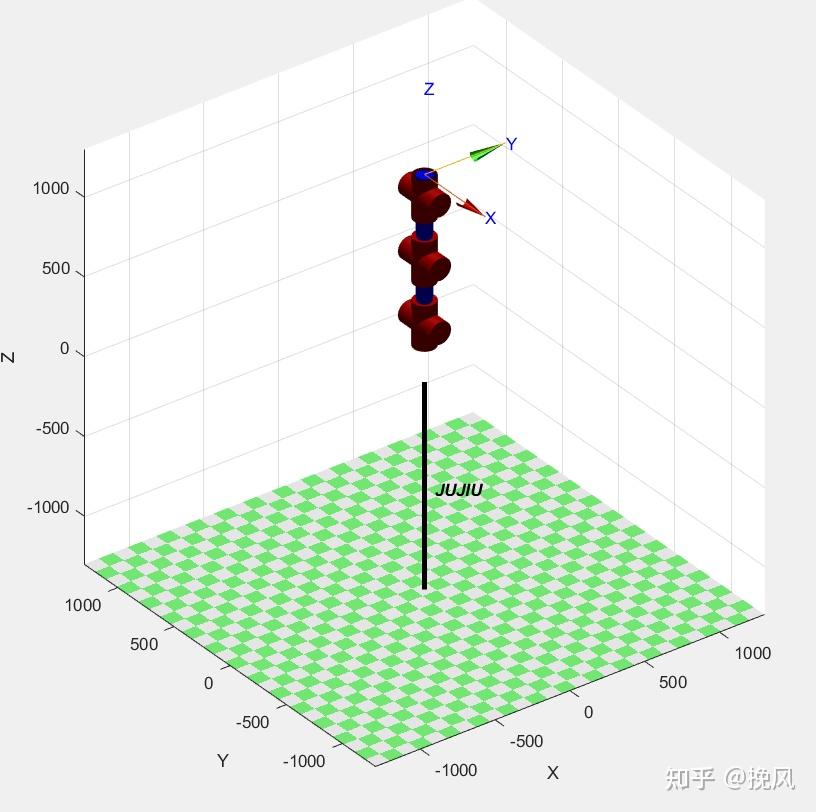
2 位姿变换
2.1 矢量矩阵表达
按照前述建立的坐标系,空间中点的位置可以用3×1的位置矢量对任意点进行定位:
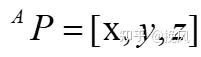
空间中物体的姿态用三个单位矢量,或者一个3×3的矩阵来表示,每一列为坐标系的轴矢量位置参量,
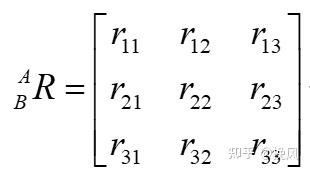
由上,一个矢量表示位置,三个矢量表示姿态,可以组合为表示位置与姿态的4×4矩阵,又称转换矩阵(和逆转换矩阵)

2.2 刚体姿态的其他表达方式
上述方式由O作为远点建立固结于刚体的正交坐标系表示刚体的位置,各坐标系的基矢量组成矢量列阵为刚体的连体基,刚体转动的不同姿态可利用连体基之间的方向余弦确定。其中,9个方向余弦元素中只有3个独立参数,体现刚体的3个转动自由度。
设刚体连体基从初始位置e出发,先绕Z轴转动ψ角到达e1,然后绕x1转动θ到达e2,最后绕z2轴转动φ达到e3.这三个广义坐标称为欧拉角,其中ψ为进动角,θ为章动角,Φ为自转角。
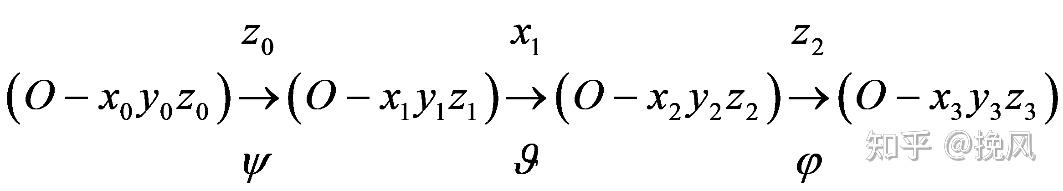
最后,欧拉角表达的转换矩阵为(网上找了5个版本,每个表达式都不一致,主要是正负号问题,所以无奈只能自己敲一个算算)
clc,clear
syms psi theta phi
Z=[cos(phi) sin(phi) 0;-sin(phi) cos(phi) 0;0 0 1];
N=[1 0 0; 0 cos(theta) sin(theta);0 -sin(theta) cos(theta)];
Z1=[cos(psi) sin(psi) 0;-sin(psi) cos(psi) 0;0 0 1];
Y=Z*N*Z1
Y =
[ cos(phi)*cos(psi) - cos(theta)*sin(phi)*sin(psi), cos(phi)*sin(psi) + cos(psi)*cos(theta)*sin(phi), sin(phi)*sin(theta)]
[- cos(psi)*sin(phi) - cos(phi)*cos(theta)*sin(psi), cos(phi)*cos(psi)*cos(theta) - sin(phi)*sin(psi), cos(phi)*sin(theta)]
[ sin(psi)*sin(theta), -cos(psi)*sin(theta), cos(theta)]另一个姿态表示法是通过四个数值来表示,称为欧拉参数,即四元数法(不在此展开)。
2.3 连杆变换
对任意给定的机械臂,连杆变换是一个变量的函数,另外三个参数由机械系统确定,对于MDH来说,坐标系2相对于坐标系1的变换次序为先绕Z轴转θ再绕X轴转α;对应SDH来说,坐标系2相对于坐标系1的变化次序为先绕X轴转α,再绕Z轴转θ。
连杆变换表达式为:
clc,clear
syms d theta a alpha
D_d=[1 0 0 0;0 1 0 0;0 0 1 d;0 0 0 1];
D_a=[1 0 0 a;0 1 0 0;0 0 1 0;0 0 0 1];
R_T=[cos(theta) -sin(theta) 0 0;sin(theta) cos(theta) 0 0;0 0 1 0;0 0 0 1];
R_a=[1 0 0 0; 0 cos(alpha) -sin(alpha) 0;0 sin(alpha) cos(alpha) 0;0 0 0 1];
%% SDH变换矩阵
T_SDH=D_d*R_T*D_a*R_a
T_SDH2=R_T*D_d*R_a*D_a
%% MDH变换矩阵
T_MDH=D_a*R_a*D_d*R_T
T_MDH2=R_a*D_a*R_T*D_d结果为:
T_SDH =[cos(theta), -cos(alpha)*sin(theta), sin(alpha)*sin(theta), a*cos(theta)]
[sin(theta), cos(alpha)*cos(theta), -sin(alpha)*cos(theta), a*sin(theta)] [ 0, sin(alpha), cos(alpha), d] [ 0, 0, 0, 1] T_SDH2 =
[cos(theta), -cos(alpha)*sin(theta), sin(alpha)*sin(theta), a*cos(theta)]
[sin(theta), cos(alpha)*cos(theta), -sin(alpha)*cos(theta), a*sin(theta)] [ 0, sin(alpha), cos(alpha), d] [ 0, 0, 0, 1] T_MDH = [ cos(theta), -sin(theta), 0, a]
[cos(alpha)*sin(theta), cos(alpha)*cos(theta), -sin(alpha), -d*sin(alpha)]
[sin(alpha)*sin(theta), sin(alpha)*cos(theta), cos(alpha), d*cos(alpha)] [ 0, 0, 0, 1] T_MDH2 = [ cos(theta), -sin(theta), 0, a]
[cos(alpha)*sin(theta), cos(alpha)*cos(theta), -sin(alpha), -d*sin(alpha)]
[sin(alpha)*sin(theta), sin(alpha)*cos(theta), cos(alpha), d*cos(alpha)] [ 0, 0, 0, 1] >>
可以发现,绕轴旋转的先后次序比较重要,而先转后偏移还是先偏移后转动则不影响结果。
将各个连杆变换矩阵连乘能得到一个坐标系相对于基坐标系的变换矩阵:
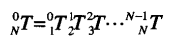
2.4 举例
- 六自由度最佳构型示例
继续以ABB的Gofa5 CRB15000为例分析,根据1.2示例列出的DH参数,可求得每一个连杆的变换矩阵:
clc
clear
%% MDH参数
A=[0,0,444,110,0,80];
Alpha=[0,90,0,90,90,-90];
D=[265,0,0,470,0,101];
%% MDH变换矩阵
syms theta
for i=1:length(A)
d=D(i);
a=A(i);
alpha=Alpha(i);
D_d=[1 0 0 0;0 1 0 0;0 0 1 d;0 0 0 1];
D_a=[1 0 0 a;0 1 0 0;0 0 1 0;0 0 0 1];
R_T=[cos(theta) -sin(theta) 0 0;sin(theta) cos(theta) 0 0;0 0 1 0;0 0 0 1];
R_a=[1 0 0 0; 0 cosd(alpha) -sind(alpha) 0;0 sind(alpha) cosd(alpha) 0;0 0 0 1];
T_MDH=D_a*R_a*D_d*R_T
end注:由于在使用matlab计算cos(pi/2)时不为0,所以更改为cosd(90),结果为0

得到的结论为:
T_MDH =
[cos(theta), -sin(theta), 0, 0]
[sin(theta), cos(theta), 0, 0]
[ 0, 0, 1, 265]
[ 0, 0, 0, 1]
T_MDH =
[cos(theta), -sin(theta), 0, 0]
[ 0, 0, -1, 0]
[sin(theta), cos(theta), 0, 0]
[ 0, 0, 0, 1]
T_MDH =
[cos(theta), -sin(theta), 0, 444]
[sin(theta), cos(theta), 0, 0]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1]
T_MDH =
[cos(theta), -sin(theta), 0, 110]
[ 0, 0, -1, -470]
[sin(theta), cos(theta), 0, 0]
[ 0, 0, 0, 1]
T_MDH =
[cos(theta), -sin(theta), 0, 0]
[ 0, 0, -1, 0]
[sin(theta), cos(theta), 0, 0]
[ 0, 0, 0, 1]
T_MDH =
[ cos(theta), -sin(theta), 0, 80]
[ 0, 0, 1, 101]
[-sin(theta), -cos(theta), 0, 0]
[ 0, 0, 0, 1]上述求出的是每一个连杆变换矩阵,将各个连杆矩阵连乘,可以得到基座和末端连杆的变换矩阵 �06
clc
clear
%% MDH参数
A=[0,0,444,110,0,80];
Alpha=[0,90,0,90,90,-90];
D=[265,0,0,470,0,101];
%% MDH变换矩阵
syms theta1 theta2 theta3 theta4 theta5 theta6
Theta=[theta1,theta2,theta3,theta4,theta5,theta6];
for i=1:length(A)
d=D(i);
a=A(i);
alpha=Alpha(i);
theta=Theta(i);
D_d=[1 0 0 0;0 1 0 0;0 0 1 d;0 0 0 1];
D_a=[1 0 0 a;0 1 0 0;0 0 1 0;0 0 0 1];
R_T=[cos(theta) -sin(theta) 0 0;sin(theta) cos(theta) 0 0;0 0 1 0;0 0 0 1];
R_a=[1 0 0 0; 0 cosd(alpha) -sind(alpha) 0;0 sind(alpha) cosd(alpha) 0;0 0 0 1];
T{i}=D_a*R_a*D_d*R_T;
end
T64=T{5}*T{6}
T63=T{4}*T64
T31=T{2}*T{3}
T61=T31*T63
T60=T{1}*T61计算结果为
T64 =[cos(theta5)*cos(theta6), -cos(theta5)*sin(theta6), -sin(theta5), 80*cos(theta5) – 101*sin(theta5)]
[ sin(theta6), cos(theta6), 0, 0]
[cos(theta6)*sin(theta5), -sin(theta5)*sin(theta6), cos(theta5), 101*cos(theta5) + 80*sin(theta5)]
[ 0, 0, 0, 1] T63 =
[cos(theta4)*cos(theta5)*cos(theta6) – sin(theta4)*sin(theta6), – cos(theta6)*sin(theta4) – cos(theta4)*cos(theta5)*sin(theta6), -cos(theta4)*sin(theta5), cos(theta4)*(80*cos(theta5) – 101*sin(theta5)) + 110]
[ -cos(theta6)*sin(theta5), sin(theta5)*sin(theta6), -cos(theta5), – 101*cos(theta5) – 80*sin(theta5) – 470]
[cos(theta4)*sin(theta6) + cos(theta5)*cos(theta6)*sin(theta4), cos(theta4)*cos(theta6) – cos(theta5)*sin(theta4)*sin(theta6), -sin(theta4)*sin(theta5), sin(theta4)*(80*cos(theta5) – 101*sin(theta5))]
[ 0, 0, 0, 1] T31 =
[cos(theta2)*cos(theta3) – sin(theta2)*sin(theta3), – cos(theta2)*sin(theta3) – cos(theta3)*sin(theta2), 0, 444*cos(theta2)]
[ 0, 0, -1, 0]
[cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2), cos(theta2)*cos(theta3) – sin(theta2)*sin(theta3), 0, 444*sin(theta2)]
[ 0, 0, 0, 1] T61 = [ cos(theta6)*sin(theta5)*(cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2)) – (sin(theta4)*sin(theta6) – cos(theta4)*cos(theta5)*cos(theta6))*(cos(theta2)*cos(theta3) – sin(theta2)*sin(theta3)), – (cos(theta6)*sin(theta4) + cos(theta4)*cos(theta5)*sin(theta6))*(cos(theta2)*cos(theta3) – sin(theta2)*sin(theta3)) – sin(theta5)*sin(theta6)*(cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2)), cos(theta5)*(cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2)) – cos(theta4)*sin(theta5)*(cos(theta2)*cos(theta3) – sin(theta2)*sin(theta3)), 444*cos(theta2) + (cos(theta4)*(80*cos(theta5) – 101*sin(theta5)) + 110)*(cos(theta2)*cos(theta3) – sin(theta2)*sin(theta3)) + (cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2))*(101*cos(theta5) + 80*sin(theta5) + 470)] [ – cos(theta4)*sin(theta6) – cos(theta5)*cos(theta6)*sin(theta4), cos(theta5)*sin(theta4)*sin(theta6) – cos(theta4)*cos(theta6), sin(theta4)*sin(theta5), -sin(theta4)*(80*cos(theta5) – 101*sin(theta5))] [- (sin(theta4)*sin(theta6) – cos(theta4)*cos(theta5)*cos(theta6))*(cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2)) – cos(theta6)*sin(theta5)*(cos(theta2)*cos(theta3) – sin(theta2)*sin(theta3)), sin(theta5)*sin(theta6)*(cos(theta2)*cos(theta3) – sin(theta2)*sin(theta3)) – (cos(theta6)*sin(theta4) + cos(theta4)*cos(theta5)*sin(theta6))*(cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2)), – cos(theta5)*(cos(theta2)*cos(theta3) – sin(theta2)*sin(theta3)) – cos(theta4)*sin(theta5)*(cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2)), 444*sin(theta2) + (cos(theta4)*(80*cos(theta5) – 101*sin(theta5)) + 110)*(cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2)) – (cos(theta2)*cos(theta3) – sin(theta2)*sin(theta3))*(101*cos(theta5) + 80*sin(theta5) + 470)] [ 0, 0, 0, 1] T60 = [ sin(theta1)*(cos(theta4)*sin(theta6) + cos(theta5)*cos(theta6)*sin(theta4)) – cos(theta1)*((sin(theta4)*sin(theta6) – cos(theta4)*cos(theta5)*cos(theta6))*(cos(theta2)*cos(theta3) – sin(theta2)*sin(theta3)) – cos(theta6)*sin(theta5)*(cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2))), sin(theta1)*(cos(theta4)*cos(theta6) – cos(theta5)*sin(theta4)*sin(theta6)) – cos(theta1)*((cos(theta6)*sin(theta4) + cos(theta4)*cos(theta5)*sin(theta6))*(cos(theta2)*cos(theta3) – sin(theta2)*sin(theta3)) + sin(theta5)*sin(theta6)*(cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2))), cos(theta1)*(cos(theta5)*(cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2)) – cos(theta4)*sin(theta5)*(cos(theta2)*cos(theta3) – sin(theta2)*sin(theta3))) – sin(theta1)*sin(theta4)*sin(theta5), cos(theta1)*(444*cos(theta2) + (cos(theta4)*(80*cos(theta5) – 101*sin(theta5)) + 110)*(cos(theta2)*cos(theta3) – sin(theta2)*sin(theta3)) + (cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2))*(101*cos(theta5) + 80*sin(theta5) + 470)) + sin(theta1)*sin(theta4)*(80*cos(theta5) – 101*sin(theta5))] [- cos(theta1)*(cos(theta4)*sin(theta6) + cos(theta5)*cos(theta6)*sin(theta4)) – sin(theta1)*((sin(theta4)*sin(theta6) – cos(theta4)*cos(theta5)*cos(theta6))*(cos(theta2)*cos(theta3) – sin(theta2)*sin(theta3)) – cos(theta6)*sin(theta5)*(cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2))), – cos(theta1)*(cos(theta4)*cos(theta6) – cos(theta5)*sin(theta4)*sin(theta6)) – sin(theta1)*((cos(theta6)*sin(theta4) + cos(theta4)*cos(theta5)*sin(theta6))*(cos(theta2)*cos(theta3) – sin(theta2)*sin(theta3)) + sin(theta5)*sin(theta6)*(cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2))), sin(theta1)*(cos(theta5)*(cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2)) – cos(theta4)*sin(theta5)*(cos(theta2)*cos(theta3) – sin(theta2)*sin(theta3))) + cos(theta1)*sin(theta4)*sin(theta5), sin(theta1)*(444*cos(theta2) + (cos(theta4)*(80*cos(theta5) – 101*sin(theta5)) + 110)*(cos(theta2)*cos(theta3) – sin(theta2)*sin(theta3)) + (cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2))*(101*cos(theta5) + 80*sin(theta5) + 470)) – cos(theta1)*sin(theta4)*(80*cos(theta5) – 101*sin(theta5))] [ – (sin(theta4)*sin(theta6) – cos(theta4)*cos(theta5)*cos(theta6))*(cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2)) – cos(theta6)*sin(theta5)*(cos(theta2)*cos(theta3) – sin(theta2)*sin(theta3)), sin(theta5)*sin(theta6)*(cos(theta2)*cos(theta3) – sin(theta2)*sin(theta3)) – (cos(theta6)*sin(theta4) + cos(theta4)*cos(theta5)*sin(theta6))*(cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2)), – cos(theta5)*(cos(theta2)*cos(theta3) – sin(theta2)*sin(theta3)) – cos(theta4)*sin(theta5)*(cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2)), 444*sin(theta2) + (cos(theta4)*(80*cos(theta5) – 101*sin(theta5)) + 110)*(cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2)) – (cos(theta2)*cos(theta3) – sin(theta2)*sin(theta3))*(101*cos(theta5) + 80*sin(theta5) + 470) + 265] [ 0, 0, 0, 1] >>
根据 �06可得到运动学方程,输入各个关节角的角度,即可得到末端轨迹关于基坐标系的表达。
3 协作机械臂运动学位置描述
3.1 正运动学
协作机械臂的正运动学位置描述是指已知各个关节的角度,求解机械臂末端的位置和姿态。由于描述机械臂末端刚体需要3个位置参数与3个角度参数,因此对于六自由度的机械臂而言,角度关节与末端位置关系是一一对应的。
由2.4节可得正运动学方程。
3.2 逆运动学
逆运动学是已知机械臂的末端位置,求解机械臂的关节角,即知道�06求θ值。当机械臂为6自由度时,末端位置与关节角一一对应,然而由于机械臂存在几何对称的情况,串联机械臂的逆解往往不唯一,因此机械臂逆解需要在多组可行解中结合环境的约束和机械臂自身构型的约束寻找一组合理解,当机械臂自由度大于6时,机械臂逆解将有无穷多组,此时逆解求解会更复杂。
(1)解的存在性
工作空间是指机械臂末端执行器能达到的范围,如果腕部坐标系的期望位姿在工作空间内,那么至少存在一个解。
(2)多重解
末端执行器到达某一位置,可能存在多个位形,即存在多个解,对于一个全部为旋转关节的6自由度机械臂来说,可能多达16种解,通常采用无障碍条件下“最短行程”解。
(3)求解方法
机械臂的全部求解方法分为封闭解和数值解法,由于数值解法的迭代性质,要比封闭解的求解速度慢得多,具有6个旋转关节的机械臂存在封闭解的充分条件是相邻的三个关节轴线相交于一点,当今设计的六自由度机械臂几乎都是4、5、6相交。
封闭解的求解方法有两类:代数法和几何法,可详见我的博客文章。
基于Python的3R机器人运动仿真 – 挽年_Sonny – 博客园www.cnblogs.com/Sonny-xby/p/12371834.html
3.3 运动学求解程序
尽管六自由度的机器人没有封闭解,但是Pieper研究了三个相邻轴相交于一点的六自由度操作臂,可以得到封闭解。由于协作机械臂求解程序比较复杂,此处采用Robotics工具包求解.
开篇经典构型六自由度机械臂的运动学程序如下:
%%建立协作机械臂模型
% MDH参数
clc,clear
a=[0,0,444,110,0,80];
alpha=[0,pi/2,0,pi/2,pi/2,-pi/2];
d=[265,0,0,470,0,101];
for i=1:6
L(i)=Link([0,d(i),a(i),alpha(i)],'modified');
end
%连接连杆,机械臂取名
Robot_1=SerialLink(L,'name','66');
Robot_1.base=transl([0 0 0]);
Robot_1.plot([0,pi/2,0,0,0,0]);
Robot_1.display();
Robot_1.teach();
%运动学正解
for j=1:50
q=0.8*j/50*[0,pi/2,0,0,0,0]+[0,0,0,0,0,-pi/2];
T=Robot_1.fkine(q);
Robot_1.plot(q);
T_trans=double(T);
alpha_in(:,j)=q;
P_save_e(:,j)=T_trans(1:3,4);
end
figure(41),hold on,plot(alpha_in')
figure(40),hold on,plot3(P_save_e(1,:),P_save_e(2,:),P_save_e(3,:))
%运动学逆解
q_inv=Robot_1.ikine(T,'pinv')其中,定义单根连杆的方式有3种:
L = Link([0 1.2 0.3 pi/2],'modified');
L = Link('revolute','d',1.2,'a',0.3, 'alpha',pi/2);
L = Revolute('d',1.2,'a',0.3,'alpha',pi/2)4 协作机械臂运动学速度描述
4.1 时变位姿
描述点速度的大小取决于两个坐标系:微分运算的坐标系和描述速度矢量的坐标系。
上述为机械臂运动学位移量在关节空间和末端操作空间之间的转换关系,此外运动学还包括速度量在两个空间之间的转换关系,这需要首先求出描述两者速度转换关系的雅可比矩阵,对于6自由度的机械臂,雅可比矩阵为
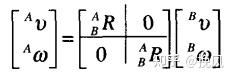





评论0