码垛机械臂的结构原理与控制算法

来源：https://zhuanlan.zhihu.com/p/703650416

0 概述

码垛机械臂一般执行抓取、打包处理、运输堆放产品等任务，当前比较流行的码垛是四轴平行四边形构型，如下图所示。为何都喜欢采用这种机构实现？这得从平衡吊的原理说起。

平衡吊的结构如图，主要分为传动、杆系和回转机构三部分，其中杆系就是平行四边形机构（DB、BC、EO、OA组成），另外O铰链位置安装有滚轮，可以沿水平导轨滚动；D位置是一个丝杠螺母结构，电机传动驱使螺母升降运动。

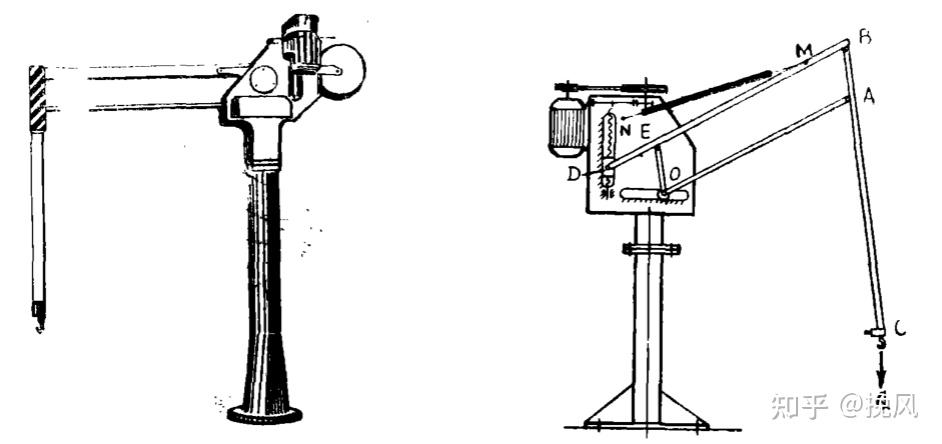
0.1 平行四边形机构结构分析

分析平行四边形机构之前，先复习一下本科理论力学的基础知识：

三力杆：根据静力学原理，平面力系中某一杆件同时受三力作用，则三力必交于一点，该杆件叫做三力杆件；

二力杆：根据静力学原理，平面力系中某一杆件同时受二力作用且二力的作用点在杆件两个端点，则二力必然大小相等方向相反，叫做二力杆。

————

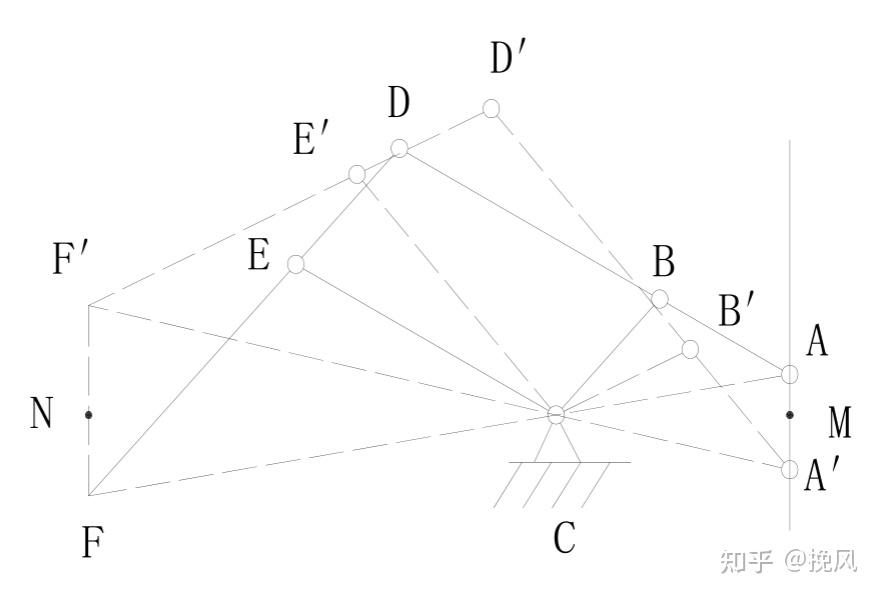
根据上面的定义，先将平衡吊简化为下面简图，其中，BC、CE为二力杆件，ABD、DEF为三力杆件，BCDE构成一个平行四边形，F为负载端。

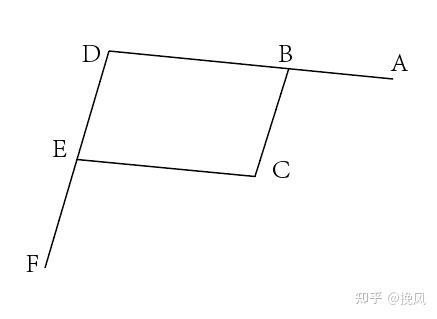
先分析DEF，其中F铰链带负载，负载重力竖直向下，CE为二力杆件，受力方向沿杆线，两条线交于一点G，再根据三力杆件的特点，所受力最终汇交于一点，因此ABD杆处D点的受力方向为图中红色实线DG；

再来分析ABD杆件，其中D铰链受力方向为DG延长线上，BC杆为二力杆件，故B铰链的受力方向沿CB杆线，两条线交于一点H，则根据三力杆件特点，A点受力方向为AH方向。

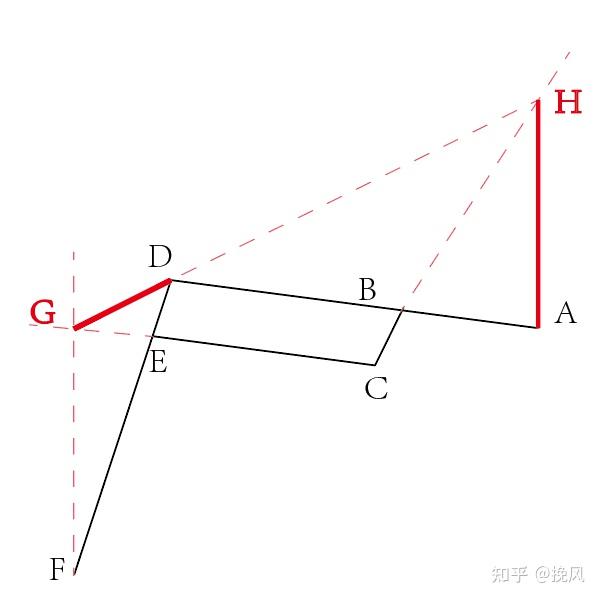
平衡吊的原理是，在受到负载F端竖直向下的重力时，无论重力多大，在整个机构上只有竖直向上的力（不包括内力），没有水平方向的分量，因此整个机构在F和A两端的受力必须都是竖直向上的。

因此，在力多边形中，FG和AH都是竖直方向的，则满足该条件的机构几何条件为：

▲GEF相似于▲ABH

▲GED相似于▲DBH

根据相似三角形的对应边成比例关系，则：

EG:EF=BA:BH

DE:EG=HB:BD

联立上式，得到：

EF:ED=BD:BA

因此，只要杆件满足该关系式，机构可在任意位置达到平衡。

此外，该机构还有一个特点，即ACF在任意姿态下三点共线（感兴趣可以证明一下，平行四边形机构决定）。

0.2 平行四边形机构运动分析

（1）当A点不动，C点移动时负载端F的运动分析

当C点移动到C’点，此时F水平移动到F’

C点移动前，▲FEC相似于▲CBA，CE/AB=EF/BC=FC/CA

C点移动后，▲F’E’C’相似于▲C’B’A，C’E’/AB’=E’F’/B’C’=F’C’/C’A

由于EF=E’F’，AB=AB’，CE=C’E’，BC=B’C’，故移动前后杆件比值是相同的，且移动前后，F点是水平移动的，即FN=F’N’，F的移动速度是C点移动速度的固定倍数λ（这个倍数为DF总长/DE长度）

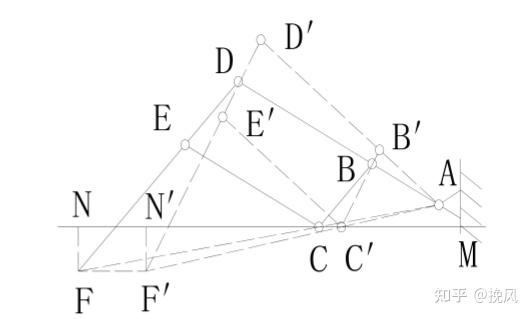
（2）当A点移动时，C点不动，F点的运动规律

当A移动到A’位置，此时F移动到F’，同上分析，由相似三角形得到F会在垂直方向上运动，其移动速度为A点移动速度的（λ-1）倍

0.3 各杆件截面尺寸设计

平行四边形机构的分析除了杆件长度及结构尺寸比例、两端点移动方向和移动速度的分析外，还需要通过动力学受力分析进行确认连杆实际的截面尺寸。

对连杆进行受力分析，三力杆分别受到重力、杆件支撑力和另一端的拉力，弯矩图大致形状如下，最大截面常出现在二力杆支撑位置，当连杆在移动过程中，弯矩值会变化，直到该杆件水平时达到最大，因此整个连杆的截面尺寸在该处为危险截面，确保此处的弯曲强度满足条件即可。

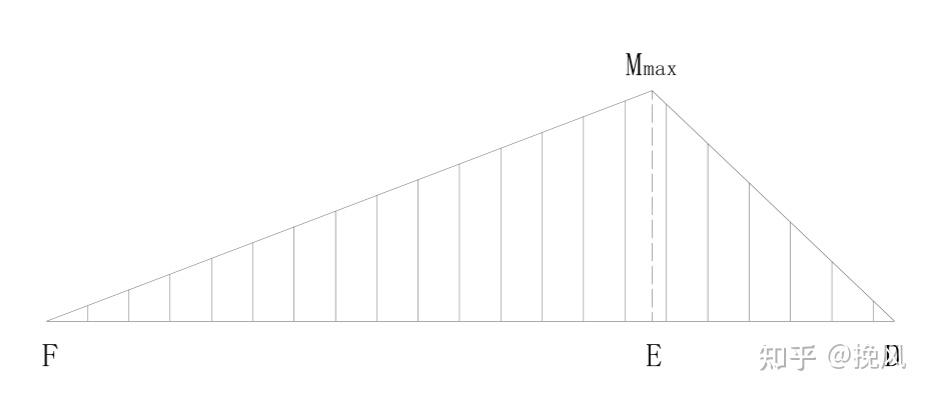
对于二力杆来说，受到的都是沿轴线方向的压力，没有受到弯、扭作用，此时需要校核连杆的压缩强度即可。

0.4 杆件自重对失衡力的影响

以上的平衡及运动分析都是假设杆系的自重及各个铰链点的摩擦忽略不计，但实际上杆件的自重、摩擦力均存在，其中自重很容易破坏平衡作用，因此失衡力是指自重作用下产生在C点产生的水平分力。

（1）DEF杆自重G1作用下，BC、CE为二力杆，故DEF自重下由三力汇交一点，可绘制受力三角形；最终在C铰链位置的受力如图中下位置，由于EC和BC杆的受力方向与大小无法水平抵消，故C点存在水平分量。

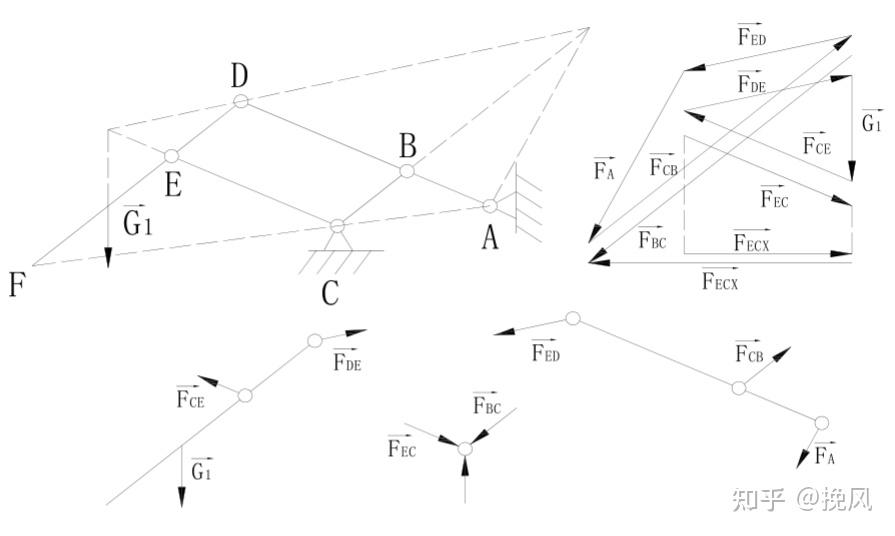
（2）ABD杆自重G2，A点和BC杆受力，同样绘制受力三角形，此时D铰链位置不受力，可见CE和DEF为0力杆（内力为0），则C点铰链所受的水平分力为BC杆在水平方向的分量

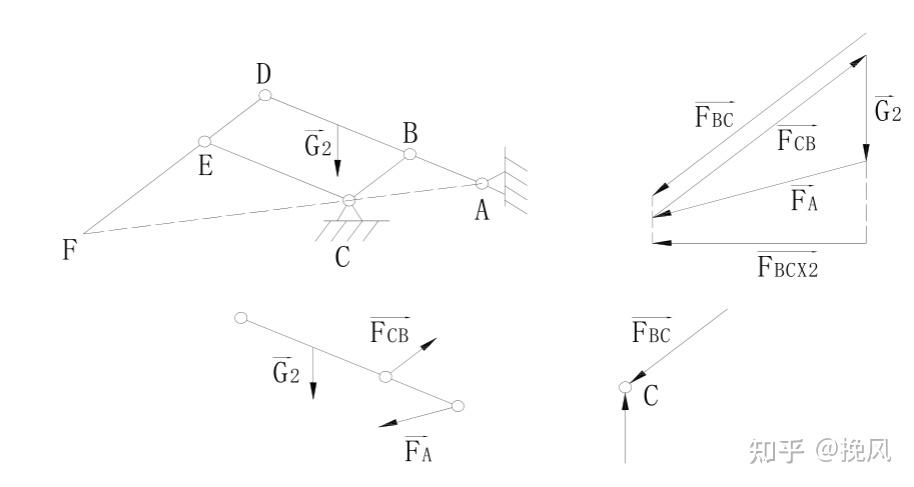
（3）CE杆自重G3，则CE杆异化为三力杆，DE异化为二力杆，BC杆仍为二力杆，受力三角形为下图，此时C铰链受BC杆分量和CE杆水平分量形成水平失衡力。

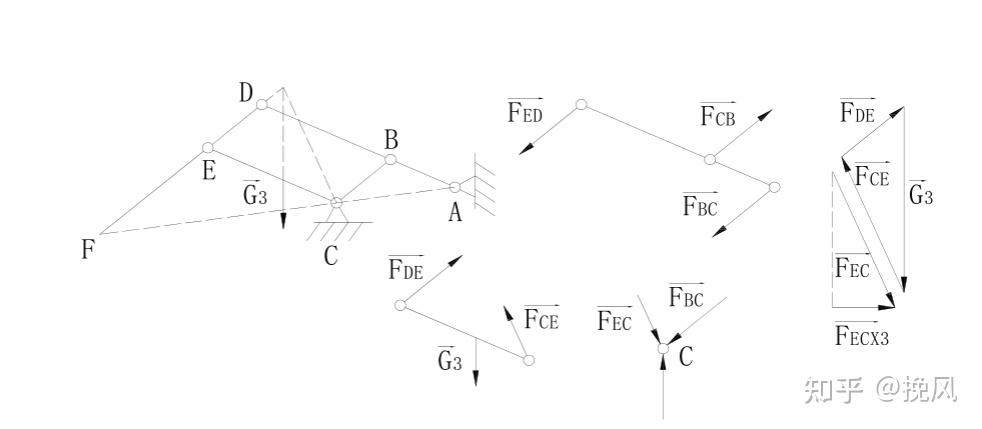
（4）BC杆自重为G4，DEF杆和CE杆为0杆，AB为二力杆，此时C受BC杆水平分量，受力分析如下图。

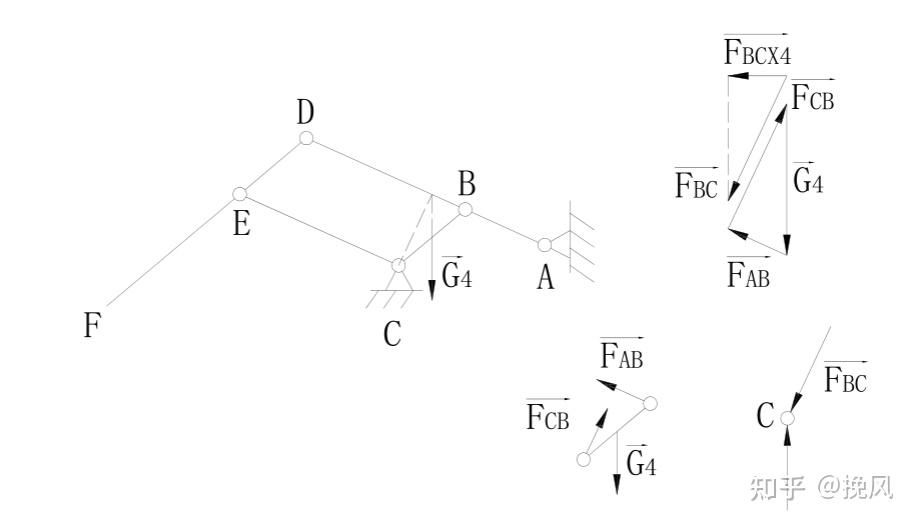
（5）消除自重引起的失衡措施

由上可见，自重引起的失衡力客观存在，常通过在A延长线上施加配重GP来平衡杆系的自重。

需要先将各连杆自重等效在ABD杆上，然后根据ABD杆的力矩平衡计算配种Gp即可。

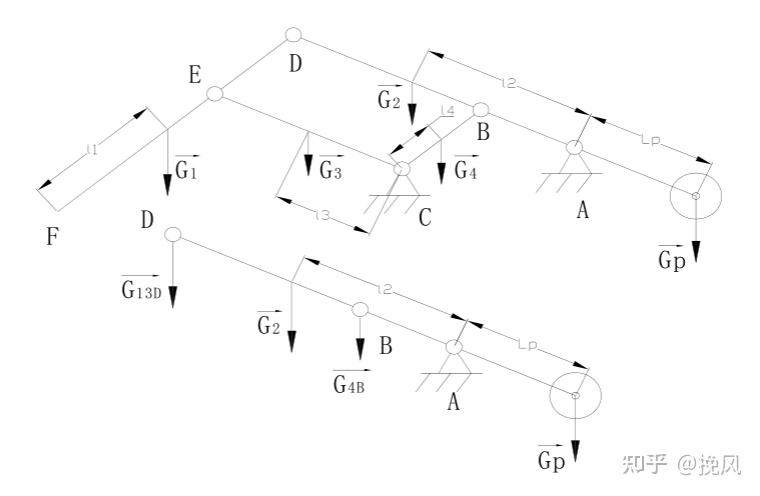
补充机械原理中“质量代换法”基础——质量代换的三个条件为：

a.代换前后杆件的质量不变

b.代换前后杆件的质心不便；

c.代换前后杆件对质心的转动惯量不变。

——————

有了以上基础理论，码垛平行四边形连杆机构就显得简单了许多。码垛机械臂的技术储备包括结构设计及优化（结构仿真与轻量化设计、静力学及动力学研究）和运动特性分析（运动学、残余振动抑制、工作空间求解、动力系统控制与轨迹优化）。通过调研大量论文和技术文章，针对上述两方面内容进行学习，总结如下。

1 结构设计

参照常规机械臂设计思路，列出码垛机械臂的结构设计流程，如图13所示。为保证码垛任务，首先需要分析其工作环境和工艺流程，以设计机械臂的整体结构，然后依据关节功能要求对机械臂关节结构尺寸进行设计。

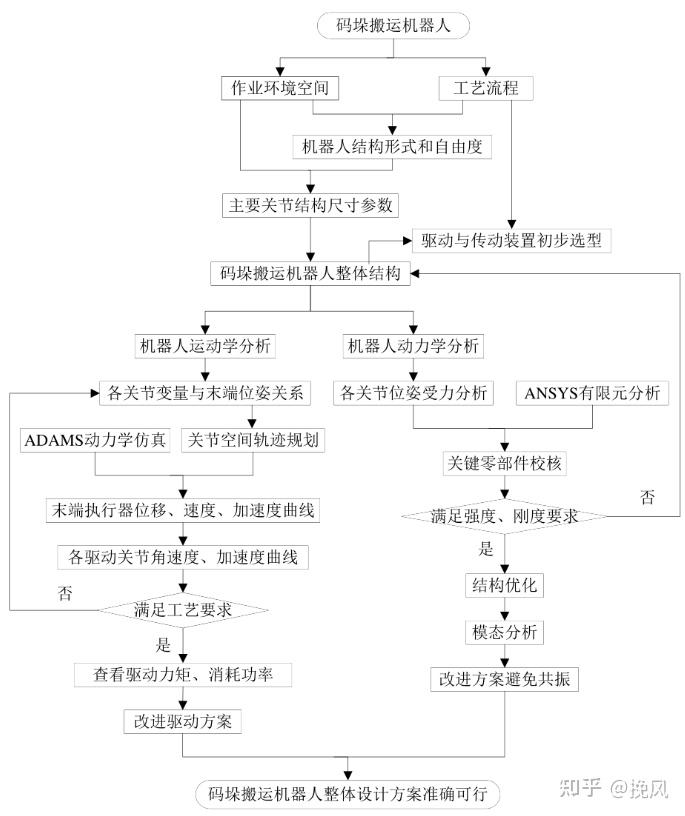
需要注意的是：

（1）灵巧轻量化设计：码垛机械臂工作环境一般为加工车间的生产线，要求机械臂的空间结构实现既定轨迹运动的同时，还要尽可能满足结构体积小、重量轻来满足复杂的生产环境；

（2）安全稳定性设计：码垛机械臂在工作时需要高速反复执行一个动作循环，能够保证每次搬运动作都准确到位对于整个生产过程的连贯性有很大意义。

1.1 码垛工作流程

码垛动作的步骤大致为：大臂、小臂、手腕探前到货物上方——末端执行器抓取货物——小臂抬起——腰部绕轴回转——腕部绕轴回转调整姿态——小臂达到码垛点——末端执行器打开放下货物，具体可参看下方视频

砖厂机械臂码垛工作视频 码垛机器人 全自动码垛机生产厂家_哔哩哔哩_bilibili​www.bilibili.com/video/BV1n44y1a7qE/?vd_source=9f64027315e62c097583861cff4be87b

基于码垛任务的实际需要，码垛机械臂通常具有四自由度，每个自由度动作关节为：腕部回转保持末端夹持爪平衡、机械臂的大臂/小臂两个转动轴转动抓取物料、腰部旋转调整位置，以上共4个自由度，全部是转动关节，如图14所示。

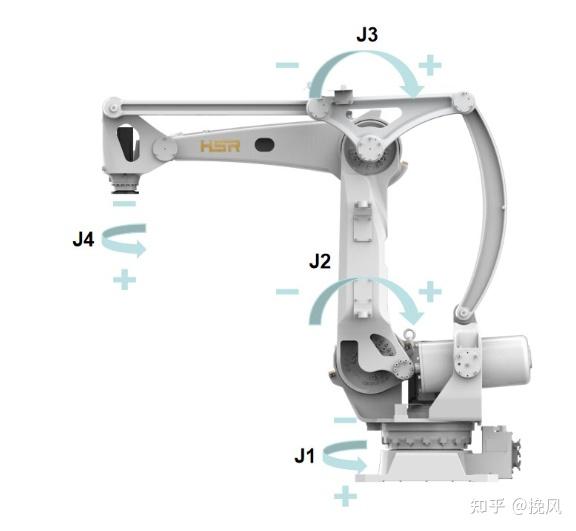
1.2 基本连杆尺寸确认

1.2.1 正向设计

正向设计思路应当根据所需要完成搬运任务空间的大小来决定该机械臂的基本连杆尺寸参数,此处仅给出理论分析，不做展开说明。

首先假设大臂、小臂连杆长度分别为 、�2、�3 ，大臂和小臂的转角 、�2、�3 ,以大臂、小臂转角的正负极限分别作图，得到以下工作空间（黑色曲线范围）。

机械臂末端可达位置 （）�（�,�,�） 为：

�=�2����2+�3����3

�=0

�=�2����2+�3����3

注：计算未计入二轴相对于基座的偏置距离

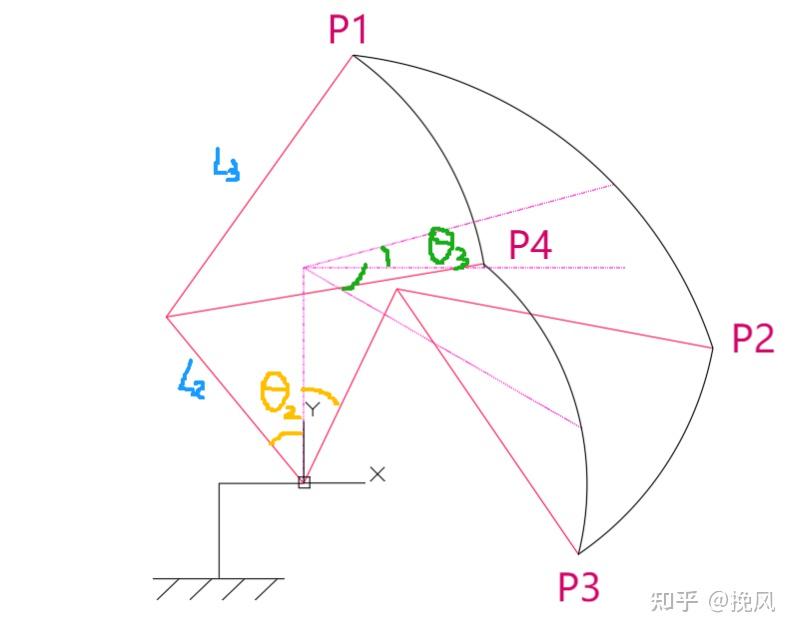
根据应用所需的空间范围，可确定 、、、�1、�2、�3、�4 的坐标。

�1=�2����2���+�3����3���

�1=�2����2���+�3����3���

�2=−�2����2���+�3����3���

�2=�2����2���+�3����3���

�3=−�2����2���+�3����3���

�3=�2����2���−�3����3���

�4=�2����2���+�3����3���

�4=�2����2���−�3����3���

由上可计算出各参数取值：

�2���=����−1����−�����+�

�2���=�−����−1����−�����+�

�2=�3−�2����2���−����2���

�3=(�3+�2����2���)2+(�3−�2����2���)2

�3���=����−1�4−�2����2����4+�2����2���

�3���=����−1�2−�2����2����2+�2����2���

其中，

�=����−1�2−�3�2−�3

�=�32+�32−�42−�42

�=(�+�−�)(�−�)

�=��−�

�=2(�4−�3)(�3−�2)

�=2(�3−�4)(�3−�2)

�=2(�3−�4)�1

由上，可确定机构的结构尺寸。

不过，当前基本上是逆向设计，通过竞品分析等方式直接确认各结构尺寸，以减少市场信息的重复试错。

1.2.2 逆向设计

事实上，竞品的运动空间图是六段线位的图形，如下所示，将竞品的工作空间图大致可以划分为pos1-6六段范围。

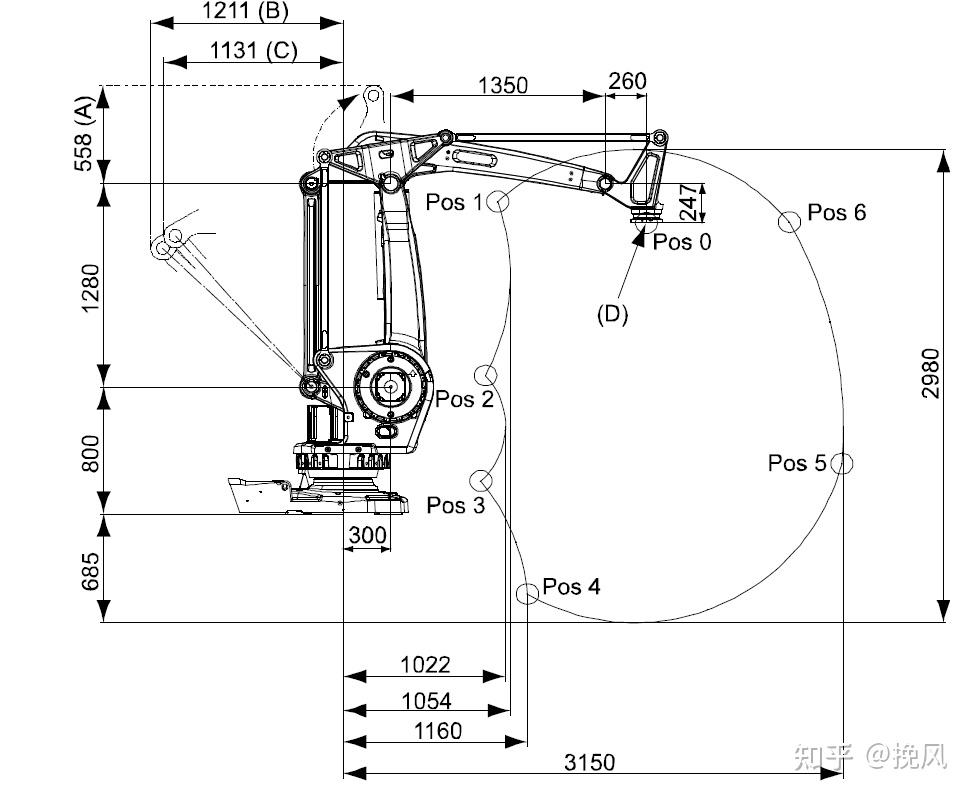
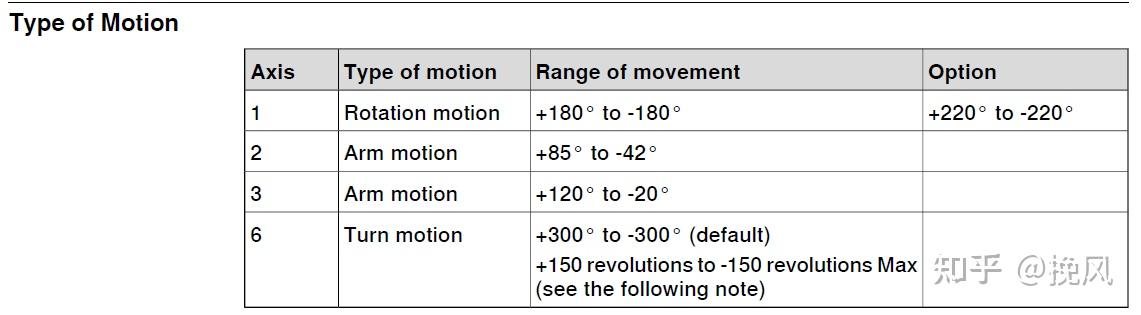
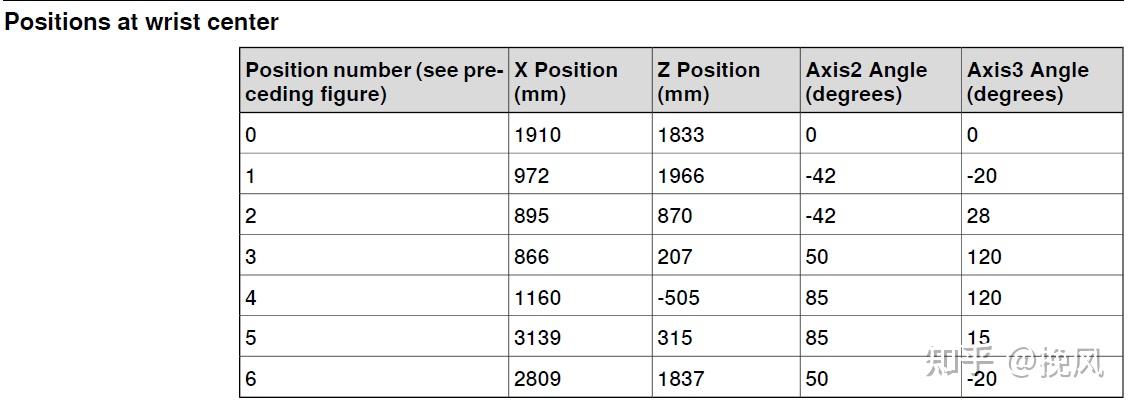
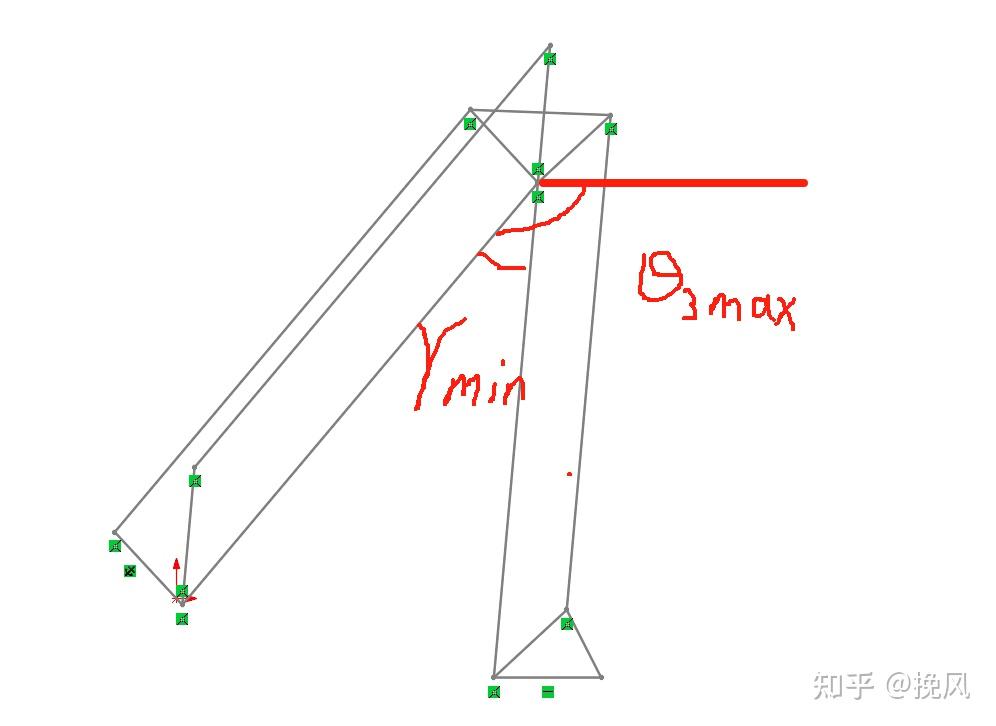
拆解竞品工作空间图时，需要对两个方面进行定义，首先是2、3轴运动范围的角度（分别定义为θ2min，θ2max，θ3min，θ3max）；常规来说，单轴的角度以相对零位姿态为0度，但是此处3轴以相对水平方向为绝对0度，当3轴相对于零位标定位置发生相对运动时，只要保持水平，此刻仍为0度。

第二个定义是二三轴运动干涉角：由于采用连杆机构，实际连杆由于机械干涉，无法转动至共线姿态，故而存在二轴和三轴最大、最小干涉角度姿态，分别定义为γmax和γmin。

（1）当2轴运动到θ2min时，此时，小臂和大臂连杆之间的夹角需大于干涉角γmin，否则θ2min给定的不合理。在该条件下，3轴的实际可达角度（相对于水平线）为：

向上仰角θ3min——图16a的pos1点

向下转角90°-θ2min-γmin（式中θmin为绝对值，无符号）——图16a的pos2点

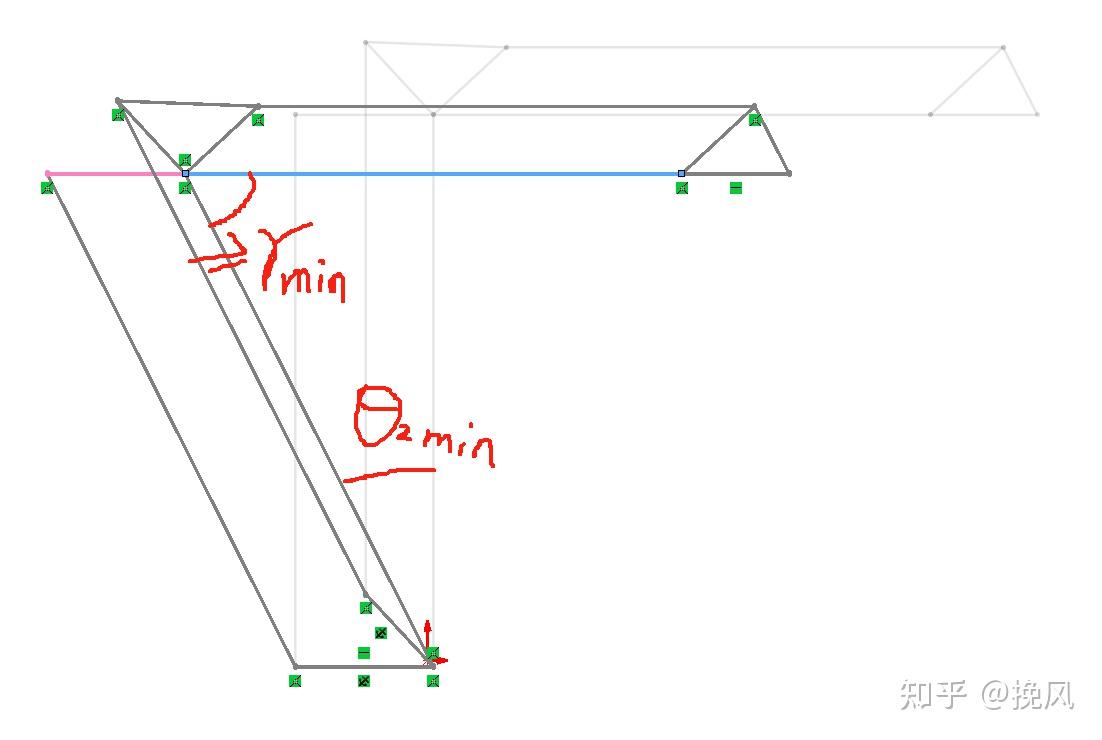
（2）当3轴运动到θ3min时，此时，2轴的极限角度为

向左仰角为 θ2min——图16a的pos1点

向右摆角为 γmax-θ3min-90°——图16a的pos6点

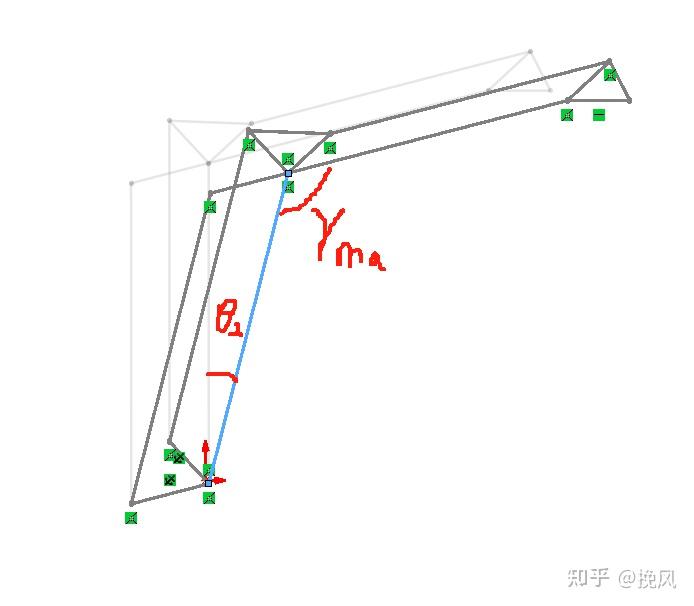
（3）当二轴运动到θ2max（假设＞90°）位置，此时θ3的极限角度为

向上仰角：270°-（γmax+θ2max）——图16a中的pos5点

向下转角：θmax-（270°-（γmax+θ2max））——图16a中的pos4点

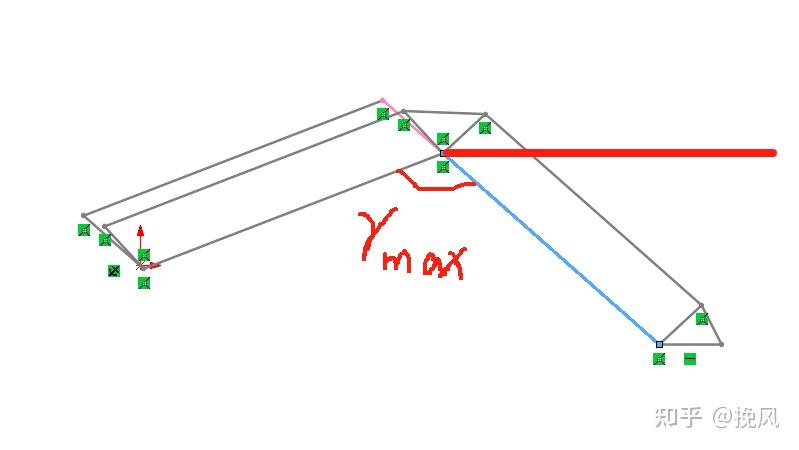
（4）当3轴运动到最小干涉角时，θ的极限角度为

向上仰角：θ2min——图16a的pos2点

向下摆角：θ3max-γmin-90°——图16a的pos3点

由上，可得码垛机构的实际运动空间图，可依据以上条件构建几何公式，进而解算合适的杆件长度。

1.3 机构设计

由调研学习，常见的码垛搬运机械臂由平行四边形辅助连杆机构协同工作，保持自平衡，图21-23为码垛机械臂结构示意图：码垛机械臂通过在肩部串联两个平行四边形结构使得腕关节始终与地面垂直，从而使被抓持物始终处于水平状态；腕部结构简单，没有姿态调整结构，仅保留末端法兰的回转运动；其中第3关节的电机和减速机构采用后置式的平行四边形机构，可以把前三个关节的电机、减速器机构放置在底座和主构架上，将明显改善系统的动态特性和降低系统的运动惯量。

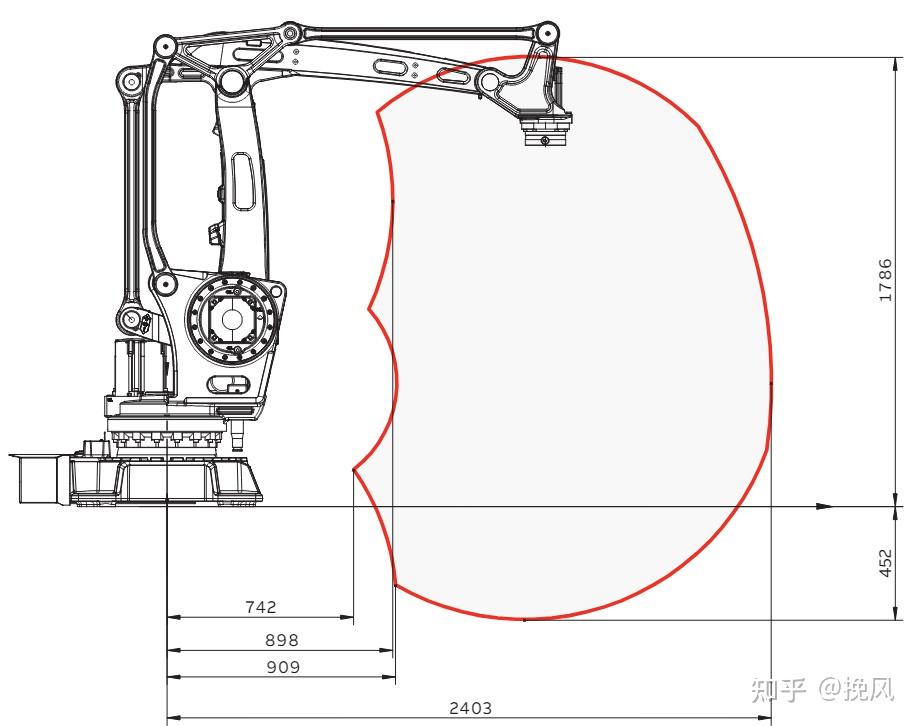
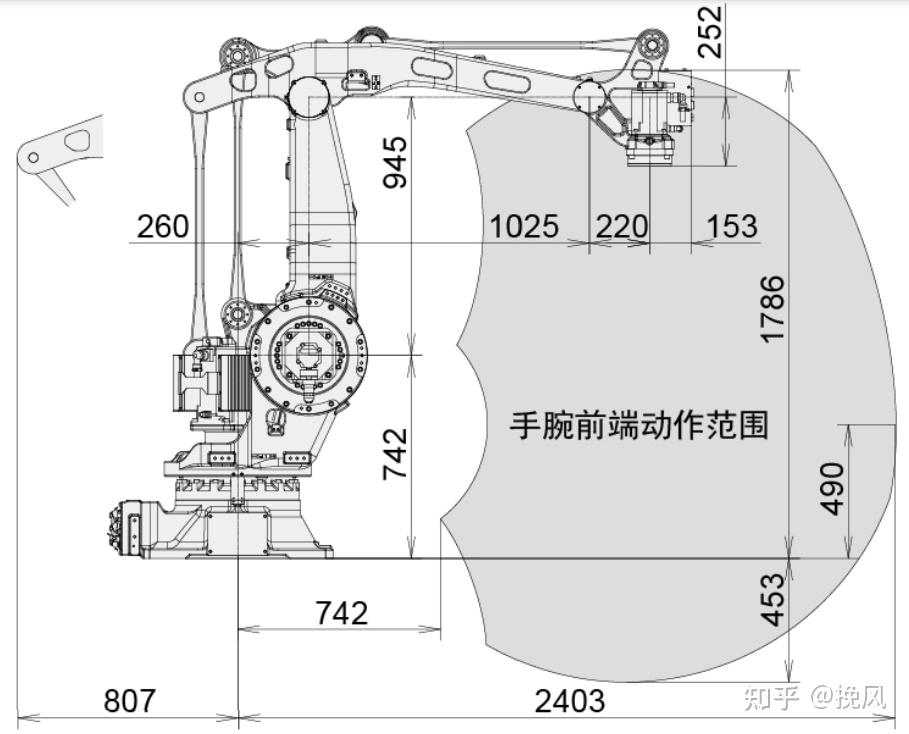
安川MPL160码垛机器人模型如下

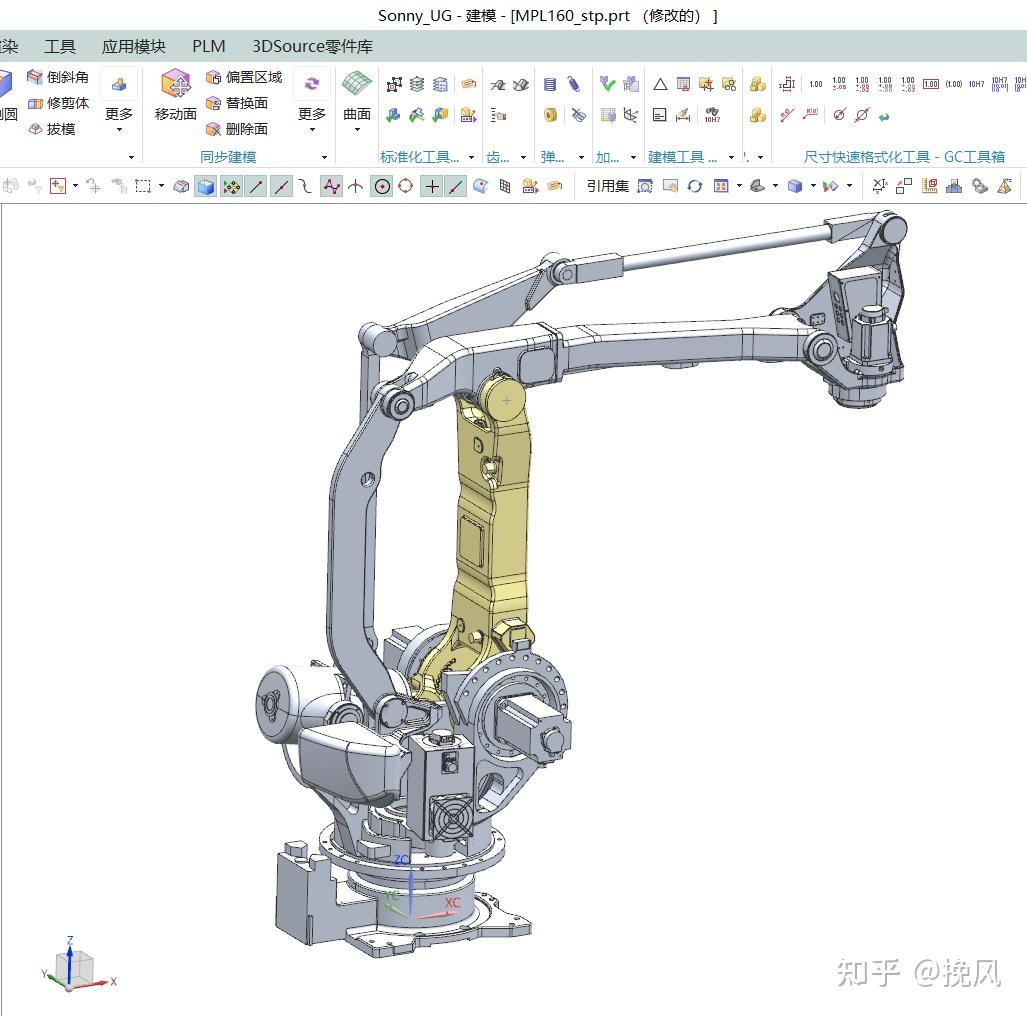
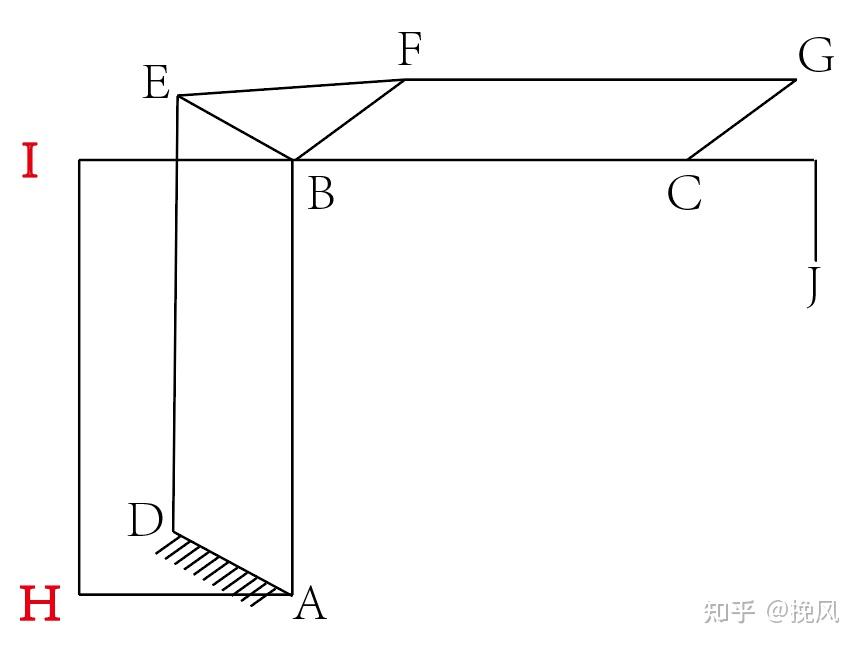
对以上机构进行总结整理，可见大臂、小臂电机都采用置于腰部而不是上下分置的方案，这样做的好处是平衡配重、减小大臂受力，缺点是需要连杆传递力矩。机械臂共需要四台伺服电机，分别为腰部电机、大臂电机、小臂电机和腕部电机，这四台电机提供了机械臂的四个自由度驱动，可绘制机构简图如图25所示，其中A点为二轴旋转中心，B点为3轴旋转中心（但是通过AH连杆驱动，图中用红色字母表示），IBC为一根杆件。

码垛机构的结构特点为：无论AB杆件摆动还是AH杆件摆动，CGJ杆件的角度适中保持不变；码垛机构的动力学特点为：AB杆件和AH杆件的摆动实现CGJ的水平和竖直合成运动。

根据机构简图可计算的自由度

�=3×8−2×11−0=2

注：以上自由度未计入腰部和腕部的2个自由度。

1.4 机构运动原理

机构主体结构是基于平衡吊原理的连杆机构，可在Solidworks中制作连杆进行拖动可视化查看，制作方式参考下文。

挽风：从0到1 | 平面连杆机构是怎么设计出来的？8 赞同 · 0 评论文章

按照结构型式在solidworks中绘制连杆并制作块，由上分析，可知该机构有2个自由度，固定其中的一个自由度，让大臂进行摆动，查看末端姿态变化。

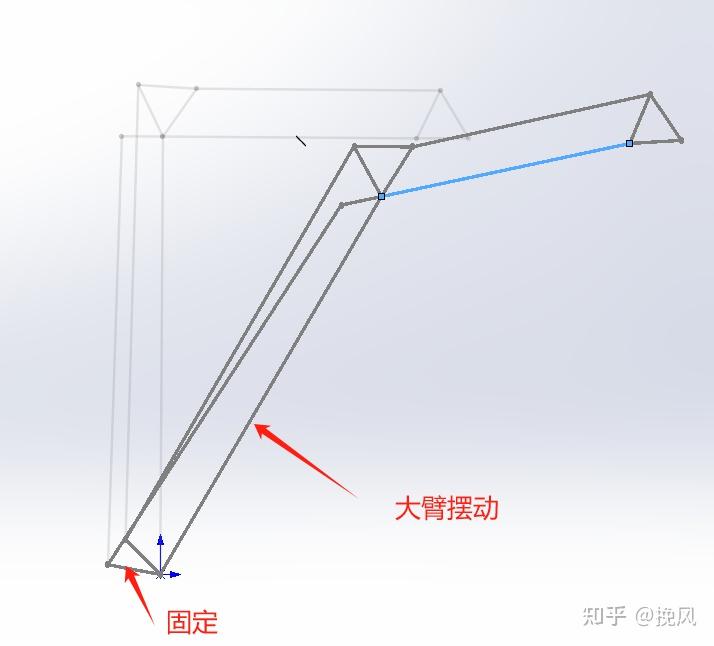
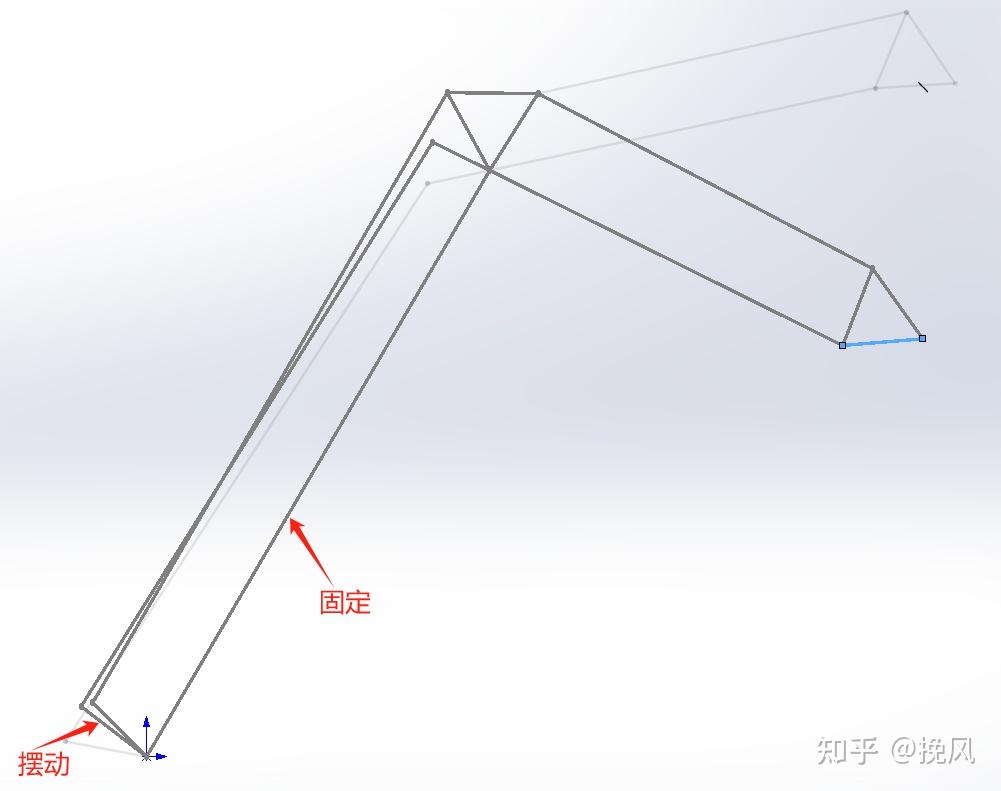
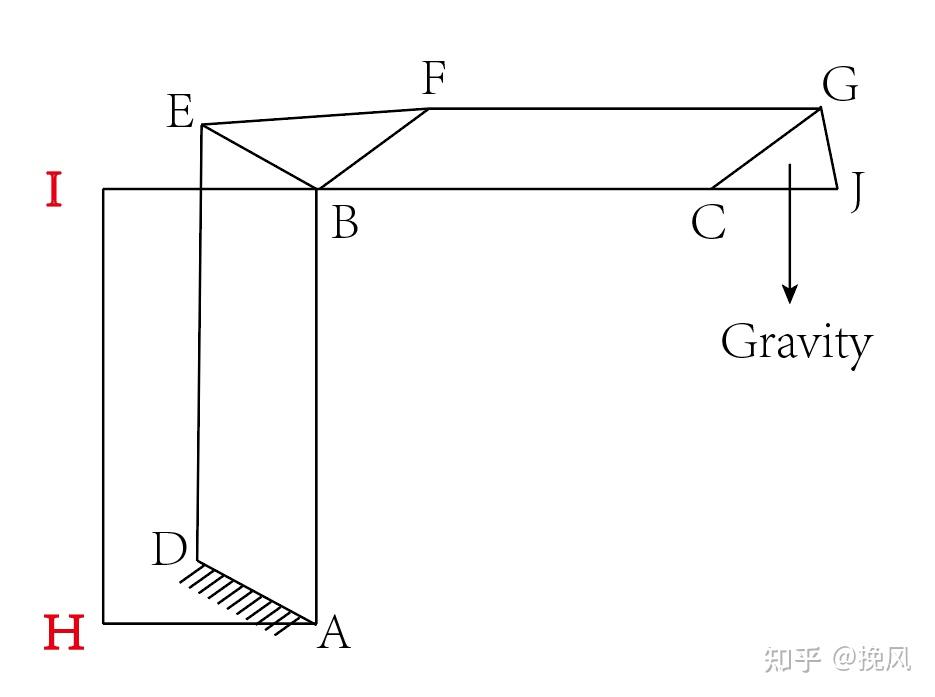
注意到，除了连杆机构的相对运动外，码垛机械臂的特点是末端执行机构始终保持竖直向下，因此竖向和横向的两个连杆机构需为平行四边形方才可实现末端位姿，可分别对比图26、27、28.

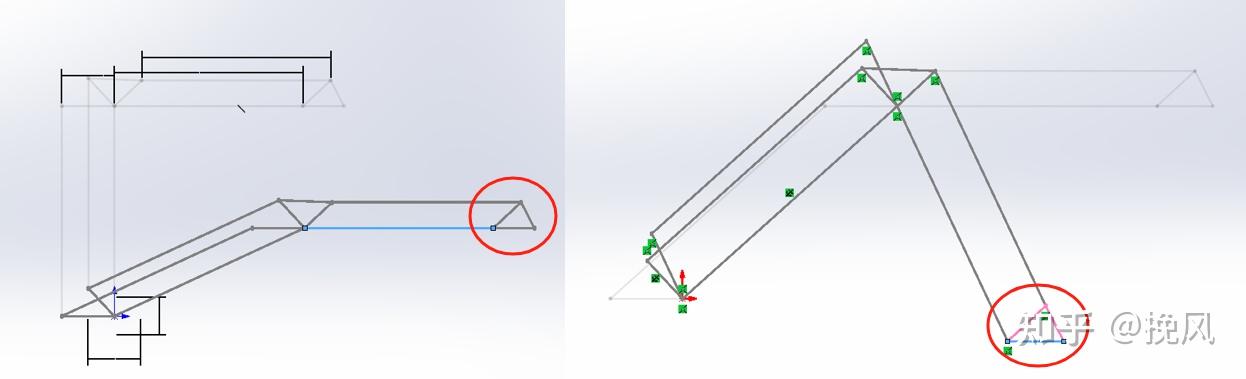
根据上述简图开始分析

（1）末端姿态始终保持水平的几何条件

假设各杆件的自重及回转中心的摩擦力为零，仅存在末端负载，则AB杆件转动角度α1时，姿态为

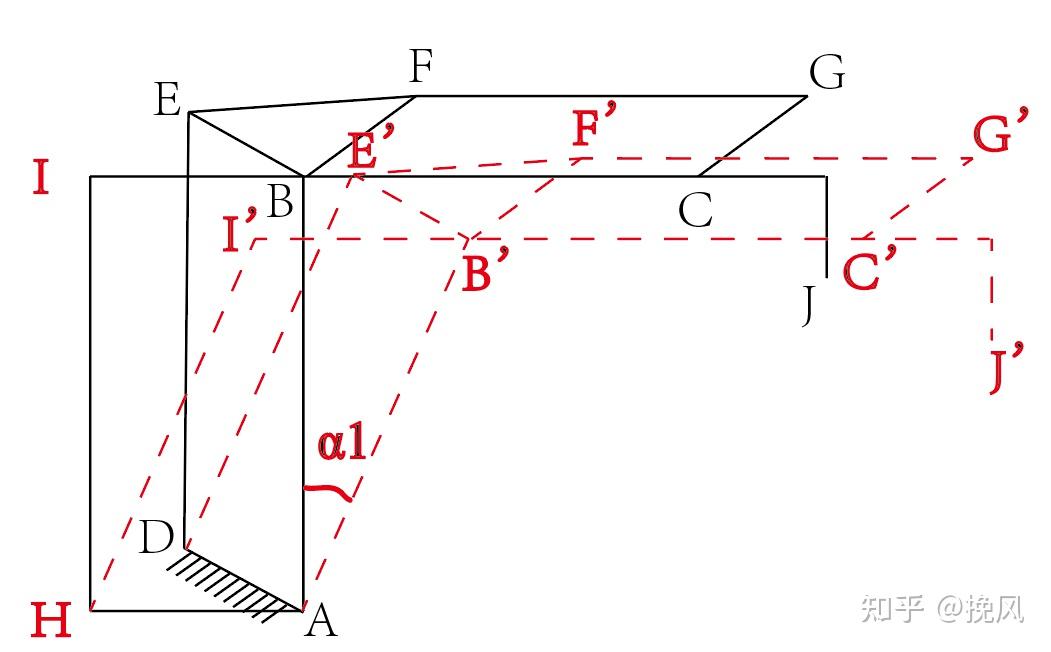
如图，B点移动至B’点，由于AD杆件与水平线固定为某一角度值，故BE、CG杆件移动后与水平线的夹角仍为固定该角度值，这保证了CGJ末端手腕不随旋转中心而变化。这要求连杆结构满足：

∠DAH+∠EBF+∠GCJ（J为竖直延长线与C延长线交点）=180°

（2）连杆受力分析

先假设连杆自重、转轴摩擦力均为0，则从末端负载开始分析，构件CJG受到竖直向下的重力

a.手腕静力分析

b.

1.5 驱动力计算

（1）基座回转驱动

基座回转的转动力主要考虑动态转矩，由腰部转台、大臂、小臂和腕部及负载绕基座回转轴线的转动力矩组成（暂不考虑摩擦力矩）

�1−���=(��1+�1�12+��2+�2�22+��3+�3�32+��4+�4�42)�1

其中， ��1 为部件的绕自身质心轴线的形状惯量， �1�12 为各部件自重到基座轴线的转动惯量（平行轴定理）

（2）大臂、小臂回转驱动

小臂和大臂的回转驱动包含静态力矩和动态力矩两大部分，其中，静态力矩计算最大负载的情况下：

�2���−������=�2��2+�3��3+�4��4

�2����������=(��2+�2�22+��3+�3�32+��4+�4�42)�2

�2���=�2���������+�2����������

（3）手腕回转驱动

手腕驱动末端执行器抓取货物后回转调整姿态，则

����=����������

2 运动分析

为了更为准确的分析码垛机械臂的运动状态，需要对各关节的位置、姿态以及各关节之间的相对运动进行描述。当前很少能找到分析码垛构型的运动学模型，一些论文里的DH参数构建方式仍然是以传统六轴的开链构型进行构建，该方法简化了被动构件和平行四边形闭式链关联连杆，机器人的运动将引入较大的误差（但也能运行），这种标称运动学模型不再于真实的机器人模型相对应。

clear;
clc;
L1=Link('d',0.26,'a',0,'alpha',pi/2);
L2=Link('d',0,'a',1.4,'alpha',0,'offset',pi/2);
L3=Link('d',0,'a',1.382,'alpha',-pi/2,'offset',-pi/2);
L4=Link('d',0,'a',0,'alpha',0);
b=isrevolute(L1);
robot=SerialLink([L1,L2,L3,L4]);
robot.name='码垛机械臂';
theta=[0 0 0 0];
robot.plot(theta);

此处学习了具有封闭运动链的机器人运动学模型，建模方法总结如下。

2.1 正运动学

机器人D-H表示法是在各关节上建立一个固定坐标系，然后利用4×4的齐次转换矩阵描述相邻两关节之间的空间位置关系，最后按照矩阵变换的方法推导出末端夹爪相对于基坐标系的空间位姿，建立起码垛机械臂的运动学模型。

（1）运动学建模

封闭链运动学模型的第一步需要建立参考坐标系统，在实际构型上分配关节参考系，并确定齐次变换坐标矩阵的必要参数。

如图所示，为简化系统，每个关节的轴系方向都相同，与世界坐标系的XYZ方向相同。

其次，连杆整体上是关于XZ平面对称，除了2、3轴运动的部分关节在Y方向存在距离。

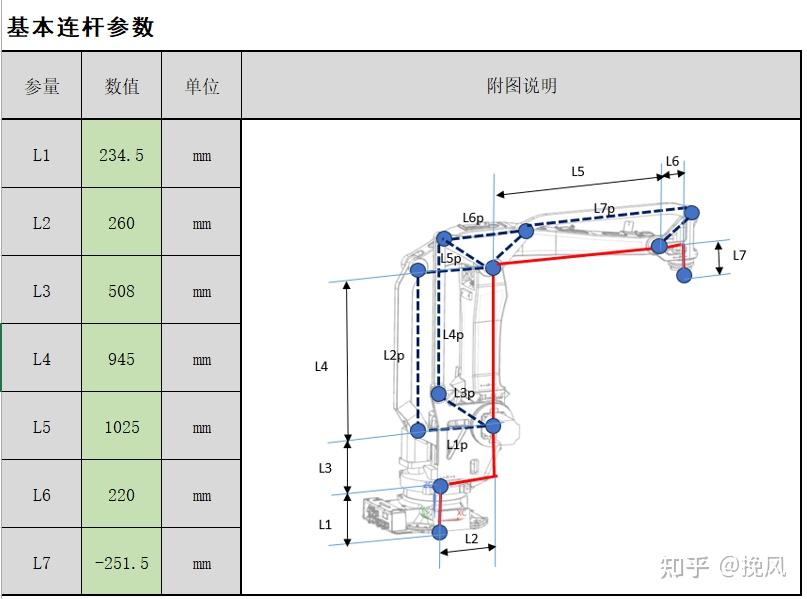
最后，L1-L7，L1p-L7p分别为连杆、闭式关联连杆的长度尺寸。

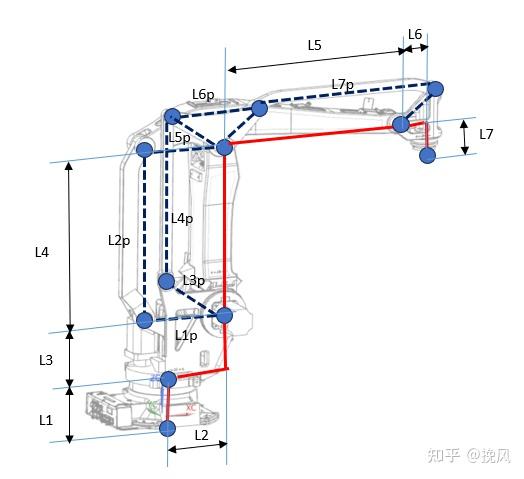
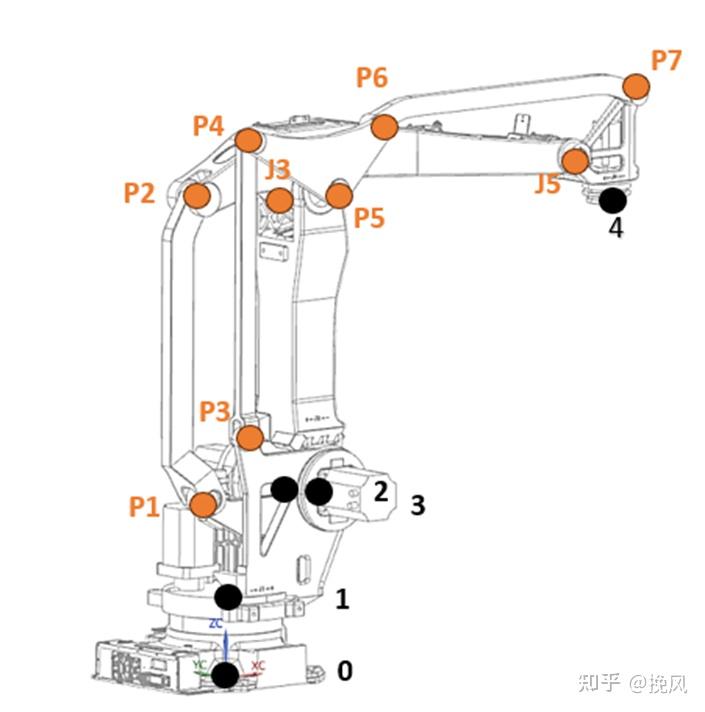
由上可知，电机共带动四个转角转动，则四个关节处分别是θ1，θ2，θ3， θ4，上图标注的P1到P7的转角分别为

p1=θ2-θ3

p2=θ3；

p3=θ2;

p4=θ3;

p5=-θ2

p6=θ3;

p7=0;

（2）构建变换矩阵

此处仍然基于机器人学中的变换矩阵，由4个独立子矩阵构成的齐次坐标变换矩阵，其一般形式如下：

�=[��;� �]

其中R为3X3的基本旋转矩阵，P为3X1的平移位置向量；η为1X3的透视向量（在运动学中为0），σ为比例因子（在运动学中为1）

（3）工具

制作了Excel工具，用于正运动学计算。

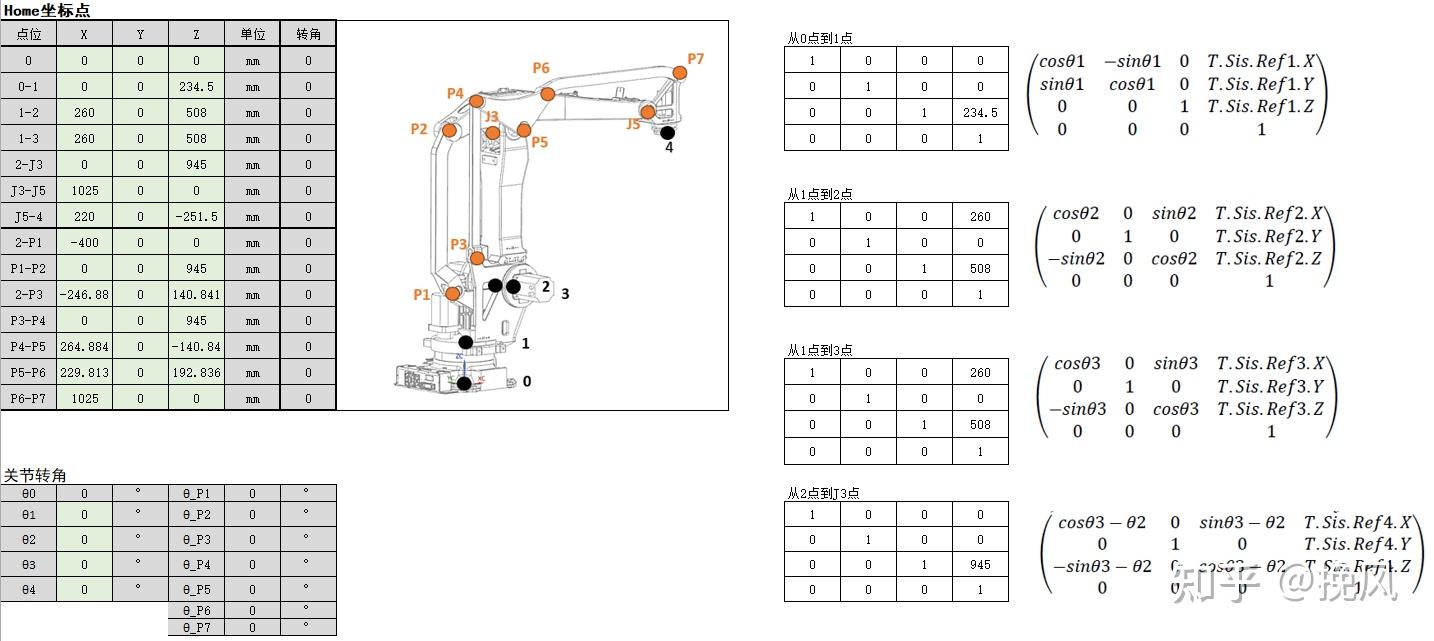
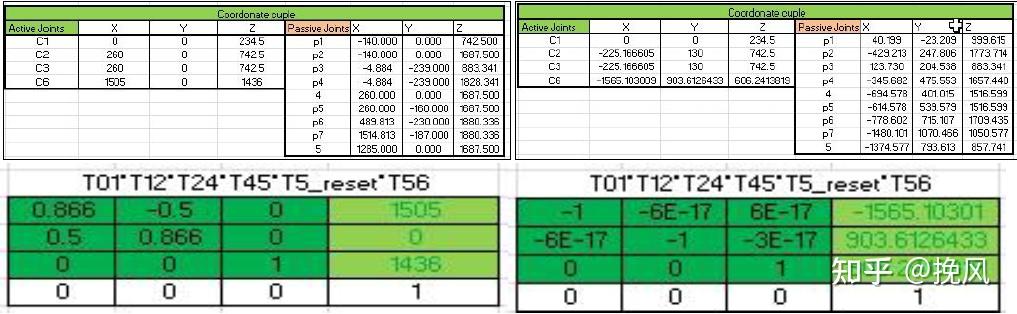
2.2 逆运动学

通常来说，逆运动学求解有解析解和数值解两种，此处用解析几何法和反变化法相结合来求解目标机械臂的运动徐封闭解：

2.3 MATLAB仿真

clear;
clc;
L1=Link('d',0.26,'a',0,'alpha',pi/2);
L2=Link('d',0,'a',1.4,'alpha',0,'offset',pi/2);
L3=Link('d',0,'a',1.382,'alpha',-pi/2,'offset',-pi/2);
L4=Link('d',0,'a',0,'alpha',0);
b=isrevolute(L1);
robot=SerialLink([L1,L2,L3,L4]);
robot.name='码垛机械臂';
theta=[0 0 0 0];
robot.plot(theta);

3 动力学分析

机器人动力学分析主要研究各关节运动的位移、速度、加速度和末端夹持爪位姿与各关节部件的驱动力和力矩之间的关系。码垛搬运机械臂动力学主要研究如何使关节在承受同等力矩作用下，能具有更好的动力且不影响关节部件的受力和平衡。

与运动学分析一样，动力学也有正、逆两个研究方向：

（1）已知作用在机器人各个关节轴所受的作用力与转动力矩，求关节处转动时的角速度、角加速度，这类问题为动力学的正向求解，主要用于仿真研究；

（2）已知各个关节转动过程中的角速度与角加速度，求在机械臂衔接部分施加的驱动力和驱动扭矩，这个过程是动力学的逆向求解。

3.1 牛顿-欧拉正向分析

运用牛顿-欧拉法将机器人动态瞬时惯性力系转化为静力系，通过分析各关节子系统之间的力系平衡方程建立机器人动态静力学模型，利用该动力学模型可以求解各关节所受约束力和未知力。

首先将码垛机械臂简化为连杆机构，对机械臂各关节进行系统受力分析，得到受力简图如下所示：

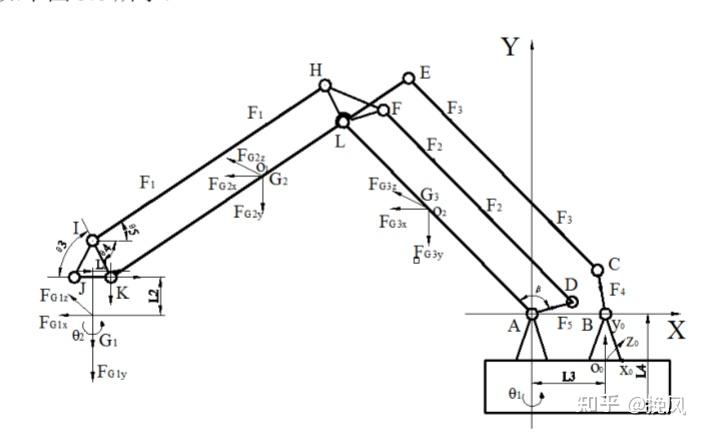
3.2 Adams正向分析

Adams仿真的求解器采用多刚体系统动力学理论中的拉格朗日方程方法，将安川MPL160码垛机器人模型导入到Admas中，设置转动约束后，在motion中添加以下函数方程：

�1=0.58875�5−2.9438�4+3.925�3−1.57

�2=0.2925�5−1.4625�4+1.95�3−0.875

�3=0.2925�5−1.4625�4+1.95�3−0.875

将该驱动方程放入ADAMS关节驱动，查看角速度与角加速度分析

3.3 逆向求解

参考文献

[1]罗杰. 码垛搬运机器人的设计与仿真分析[D].长安大学,2019.

[2]HSR-MD4110-2500 码垛机器人机械操作与维护手册 V2.0

[3]刘清辉. 高速重载码垛机器人柔性动力学建模和动态性能分析[D].兰州理工大学,2019.

[4]李渊龙. 关节式四自由度码垛机器人结构设计及仿真研究[D].燕山大学,2018.

[5] 四轴码垛机器人的机构设计及运动分析.

[6]高学恒. 4-DOF码垛机器人运动分析及轨迹规划研究[D].天津科技大学,2021.DOI:10.27359/d.cnki.gtqgu.2020.000264.

[7]DJM-1200型码垛机器人的空间机构分析与末端执行器系统设计

[8]码垛机器人机构设计与控制系统研究

[9]关节式码垛机器人运动学分析与动力学仿真

[10]ABB和kuka产品资料（该资料仅用于技术分享交流）