来源：https://zhuanlan.zhihu.com/p/1946345242811929221

本篇为第一部分，主要讨论机械臂关节空间的位置跟踪控制方法。

根据《机器人学导论》第三版（John Craig等）的机械臂控制章节，总结机械臂控制方法。并以UR5机械臂为例，在MUJOCO仿真中执行一个末端圆形轨迹，以对比不同方法的效果。

动图封面

代码仓库：github.com/DrNingZhi/robot_sim

1. 运动规划

1.1 笛卡尔空间规划

规划一个空间圆周运动（仅为实现本文的demo而实现，仅供参考）。

import numpy as np

def circular_trajectory(center, radius, rotation, dt, period):
    num_steps = int(period / dt)
    t = np.linspace(0, period, num_steps + 1)
    theta, theta_d, theta_dd = interpolation(t, period, np.pi * 2)
    pos = np.zeros((num_steps + 1, 3))
    pos[:, 0] = radius * np.cos(theta)
    pos[:, 1] = radius * np.sin(theta)
    pos[:, 2] = 0.0
    vel = np.zeros((num_steps + 1, 3))
    vel[:, 0] = theta_d * radius * np.cos(theta + np.pi / 2)
    vel[:, 1] = theta_d * radius * np.sin(theta + np.pi / 2)
    vel[:, 2] = 0.0
    acc_t = np.zeros((num_steps + 1, 3))
    acc_n = np.zeros((num_steps + 1, 3))
    acc_t[:, 0] = theta_dd * radius * np.cos(theta + np.pi / 2)
    acc_t[:, 1] = theta_dd * radius * np.sin(theta + np.pi / 2)
    acc_t[:, 2] = 0.0
    acc_n[:, 0] = theta_d**2 * radius * np.cos(theta + np.pi)
    acc_n[:, 1] = theta_d**2 * radius * np.sin(theta + np.pi)
    acc_n[:, 2] = 0.0
    acc = acc_n + acc_t
    pos = center + (rotation @ pos.T).T
    vel = (rotation @ vel.T).T
    acc = (rotation @ acc.T).T
    return t, pos, vel, acc

其中，采用5次多项式插值，从静止状态开始和结束并保证平滑。

def interpolation(t, T, p):
    A = np.array(
        [
            [T**5, T**4, T**3],
            [5.0 * T**4, 4.0 * T**3, 3.0 * T**2],
            [20.0 * T**3, 12.0 * T**2, 6.0 * T],
        ]
    )
    B = np.array([p, 0.0, 0.0])
    a = np.linalg.inv(A) @ B
    x = a[0] * t**5 + a[1] * t**4 + a[2] * t**3
    xd = 5.0 * a[0] * t**4 + 4.0 * a[1] * t**3 + 3.0 * a[2] * t**2
    xdd = 20.0 * a[0] * t**3 + 12.0 * a[1] * t**2 + 6.0 * a[2] * t
    return x, xd, xdd

1.2 机械臂运动学

将笛卡尔空间运动轨迹，转化为关节空间运动轨迹，需要通过逆运动学。简单起见，这里不调用其他运动学库，直接使用mujoco功能实现机械臂的正逆运动学。

构造RobotModel类，单独加载机械臂mjcf模型，和mujoco仿真分离，独立用于机器人模型的理论计算。

首先实现正运动学，并采用数组方法实现简单的逆运动学。此外，为了映射末端笛卡尔空间的速度与加速度，和关节空间的角速度和角加速度，需要计算jacobian及其梯度 �=��˙,�=�˙�˙+��¨

最后，后续还会用到逆动力学功能，即根据关节位置、角速度、角加速度，计算所需的关节驱动力矩，也一并实现。

import numpy as np
import mujoco
from scipy.optimize import minimize
from scipy.spatial.transform import Rotation

class RobotModel:
    def __init__(self, model: str):
        self.model = mujoco.MjModel.from_xml_path(model)
        self.data = mujoco.MjData(self.model)
        self.dt = self.model.opt.timestep
        self.dof = self.model.nv
        self.joint_lower_limits = self.model.jnt_range[:, 0]
        self.joint_upper_limits = self.model.jnt_range[:, 1]

    def forward_kinematics(self, q, body_name, point_at_body=np.zeros(3)):
        self.data.qpos = q.copy()
        mujoco.mj_kinematics(self.model, self.data)
        body_id = mujoco.mj_name2id(self.model, mujoco.mjtObj.mjOBJ_BODY, body_name)
        p = self.data.xpos[body_id]
        R = self.data.xmat[body_id].reshape((3, 3))
        p = p + R @ point_at_body
        return p, R

    def inverse_kinematics(
        self, target, body_name, q_init=None, point_at_body=np.zeros(3), smooth=True
    ):
        if q_init is None:
            q_init = np.zeros(self.dof)

        res = minimize(
            self.ik_cost,
            q_init,
            bounds=self.model.jnt_range,
            args=(target, body_name, q_init, point_at_body, smooth),
        )
        q = res.x

        err = self.ik_cost(q, target, body_name, q_init, point_at_body, smooth)
        if err > 1e-4:
            print("Warning: IK err is larger, " + str(err))
        return q

    def ik_cost(self, q, target, body_name, q_init, point_at_body, smooth):
        p, R = self.forward_kinematics(q, body_name, point_at_body)
        p_tar = target[:3, 3]
        R_tar = target[:3, :3]
        cost1 = np.linalg.norm(p - p_tar) ** 2
        cost2 = np.linalg.norm(Rotation.from_matrix(R @ R_tar.T).as_rotvec()) ** 2
        if not smooth:
            return 1000000.0 * cost1 + 3282.8 * cost2

        cost3 = np.linalg.norm(q - q_init) ** 2 / self.dof
        return 1000000.0 * cost1 + 3282.8 * cost2 + 32.8 * cost3

    def jacobian(self, q, body_name, point_on_body=np.zeros(3)):
        point, _ = self.forward_kinematics(q, body_name, point_on_body)
        body_id = mujoco.mj_name2id(self.model, mujoco.mjtObj.mjOBJ_BODY, body_name)

        self.data.qpos = q.copy()
        mujoco.mj_forward(self.model, self.data)

        jacp = np.zeros((3, self.dof))
        jacr = np.zeros((3, self.dof))
        mujoco.mj_jac(self.model, self.data, jacp, jacr, point, body_id)
        Jac = np.vstack((jacp, jacr))
        return Jac

    def jacobian_d(self, q, qd, body_name, point_on_body=np.zeros(3)):
        point, _ = self.forward_kinematics(q, body_name, point_on_body)
        body_id = mujoco.mj_name2id(self.model, mujoco.mjtObj.mjOBJ_BODY, body_name)

        self.data.qpos = q.copy()
        self.data.qpos = qd.copy()
        mujoco.mj_forward(self.model, self.data)

        jacp_d = np.zeros((3, self.dof))
        jacr_d = np.zeros((3, self.dof))
        mujoco.mj_jacDot(self.model, self.data, jacp_d, jacr_d, point, body_id)
        Jac_d = np.vstack((jacp_d, jacr_d))
        return Jac_d

    def inverse_kinematics_d(self, q, vel, acc, body_name, point_on_body=np.zeros(3)):
        Jac = self.jacobian(q, body_name, point_on_body)
        qd = np.linalg.pinv(Jac) @ vel
        Jac_d = self.jacobian_d(q, qd, body_name, point_on_body)
        qdd = np.linalg.pinv(Jac) @ (acc - Jac_d @ qd)
        return qd, qdd

1.3 关节空间运动轨迹

将1.1中得到的笛卡尔空间运动，映射到关节空间，采用上面实现的运动学功能，

def trajectory_ik(robot_model, pos, vel, acc, orientation, body_name, point_on_body):
    dof = robot_model.dof
    num_steps = len(pos)
    q = np.zeros((num_steps, dof))
    qd = np.zeros((num_steps, dof))
    qdd = np.zeros((num_steps, dof))
    for i in range(num_steps):
        target = np.eye(4)
        target[:3, 3] = pos[i]
        target[:3, :3] = orientation
        q[i] = robot_model.inverse_kinematics(
            target, body_name, q[i - 1], point_on_body, smooth=(not i == 0)
        )
        vel_a = np.array([vel[i, 0], vel[i, 1], vel[i, 2], 0.0, 0.0, 0.0])
        acc_a = np.array([acc[i, 0], acc[i, 1], acc[i, 2], 0.0, 0.0, 0.0])
        qd[i], qdd[i] = robot_model.inverse_kinematics_d(
            q[i], vel_a, acc_a, body_name, point_on_body
        )
    return q, qd, qdd

最后，生成一个末端圆形轨迹

def plan():
    mjcf_file = "ur5/ur5.xml"
    robot_model = RobotModel(mjcf_file)
    dt = robot_model.dt
    dof = robot_model.dof

    center = np.array([0.8, 0.0, 1.2])
    radius = 0.1
    rotation = Rotation.from_rotvec([0.0, np.pi / 2, 0.0]).as_matrix()
    period = 5.0

    t, pos, vel, acc = circular_trajectory(center, radius, rotation, dt, period)

    orientation = Rotation.from_rotvec([0.0, np.pi / 2, 0.0]).as_matrix()   # 机械臂末端姿态保持不变
    body_name = "wrist_3_link"
    point_at_body = np.array([0, 0, 0.05])
    q, qd, qdd = trajectory_ik(
        robot_model, pos, vel, acc, orientation, body_name, point_at_body
    )
    return t, q, qd, qdd

2. 关节空间的位置控制

2.1 关节的闭环控制。

前面已经规划出了关节的运动轨迹，对各个关节进行位置跟踪控制。最简单的方法是简化为单关节反馈闭环控制。 �=��(��−�)+��(�˙�−�˙)

一个单关节的pd控制器

class PDController:
    def __init__(self, kp, kd, limit=None):
        self.kp = kp
        self.kd = kd
        self.limit = limit

    def update(self, x, xd, x_ref, xd_ref=0.0):
        output = self.kp * (x_ref - x) + self.kd * (xd_ref - xd)
        if self.limit is not None:
            output = np.clip(output, -self.limit, self.limit)
        return output

对于整个机械臂多个关节的pd控制

class RobotPDController:
    def __init__(self, kp, kd, limit=None):
        self.dof = len(kp)
        self.joint_pd_controllers = []
        for i in range(self.dof):
            if limit is not None:
                pd_controller = PDController(kp[i], kd[i], limit[i])
            else:
                pd_controller = PDController(kp[i], kd[i])
            self.joint_pd_controllers.append(pd_controller)

    def update(self, q, qd, q_ref, qd_ref):
        tau = np.zeros(self.dof)
        for i in range(self.dof):
            tau[i] = self.joint_pd_controllers[i].update(
                q[i], qd[i], q_ref[i], qd_ref[i]
            )
        return tau

结合上述所有功能，启动mujoco仿真实现机械臂的运动

import numpy as np
import mujoco
import mujoco.viewer

mjcf_file = "ur5/ur5.xml"
model = mujoco.MjModel.from_xml_path(mjcf_file)
data = mujoco.MjData(model)
dt = model.opt.timestep
dof = model.nv

t, q, qd, qdd = plan()

# Initialize joint states
data.qpos = q[0]
data.qvel = np.zeros(dof)

# Initialize controller
kp = np.array([1000.0, 1000.0, 1000.0, 10.0, 10.0, 0.1])
kd = np.array([10.0, 10.0, 10.0, 0.1, 0.1, 0.001])
robot_controller = RobotPDController(kp, kd)

step = 0
with mujoco.viewer.launch_passive(model, data) as viewer:
    while viewer.is_running() and step < len(t):
        data.ctrl = robot_controller.update(data.qpos, data.qvel, q[step], qd[step])
        mujoco.mj_step(model, data)
        viewer.sync()
        step = step + 1

即可以得到开篇视频动画的运动效果。

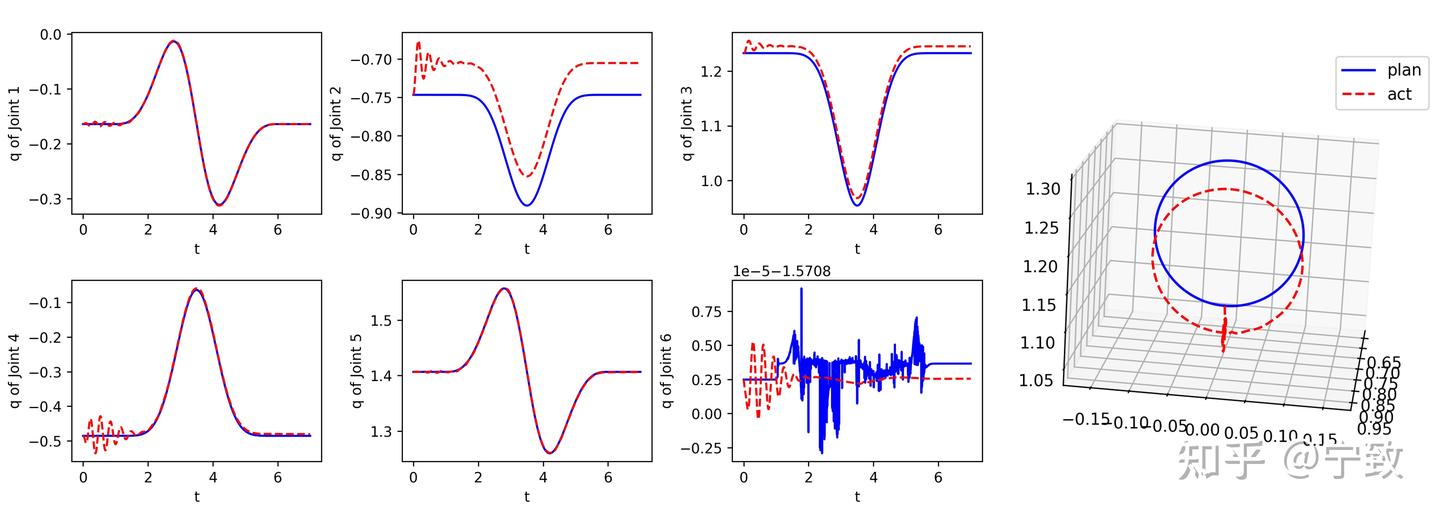
显然，由于机械臂非线性特性，这样的控制跟踪误差较大且容易不稳定。如下图所示，存在较大重力臂的关节，跟踪误差明显较大。

2.2 关节动力学前馈控制：

根据期望的运动，计算理论的扭矩值作为前馈，叠加一个pd控制器。 �=��+��(��−�)+��(�˙�−�˙)

其中 ��=�(�)�¨+�(�,�˙)+�(�)+�(�,�˙)+������

在运动速度较低时，可以只考虑重力和摩擦力。如果不考虑外力，有

��=�(�)+�(�).

无论只考虑重力还是只考虑完整的动力学，都需要准确的机械臂模型。通常情况下真实机械臂的准确模型较难获得。需要通过复杂的标定。如果模型不准确，进行动力学前馈会使跟踪效果更差，得不偿失。机械臂的标定不是本篇的主题，将在未来进一步讨论。这里，在仿真中显然模型是准确的。可以进行效果对比。

首先，只考虑重力补偿时，在RobotModel类中增加重力补偿功能：

def gravity_torque(self, q):
    self.data.qpos = q.copy()
    self.data.qvel = np.zeros(self.dof)
    self.data.qacc = np.zeros(self.dof)
    mujoco.mj_inverse(self.model, self.data)
    tau = self.data.qfrc_inverse
    return tau

然后在RobotPDController类中添加功能

def update_with_feedforward(self, q, qd, q_ref, qd_ref, tau_ref):
    tau = np.zeros(self.dof)
    for i in range(self.dof):
        tau[i] = self.joint_pd_controllers[i].update(
            q[i], qd[i], q_ref[i], qd_ref[i]
        )
    tau = tau + tau_ref
    return tau

在仿真主循环中，修改控制命令：

tau_ref = robot_model.gravity_torque(q[step])
data.ctrl = robot_controller.update_with_feedforward(data.qpos, data.qvel, q[step], qd[step], tau_ref)

即可实现PD反馈控制+重力补偿的跟踪效果（PD参数不变）：

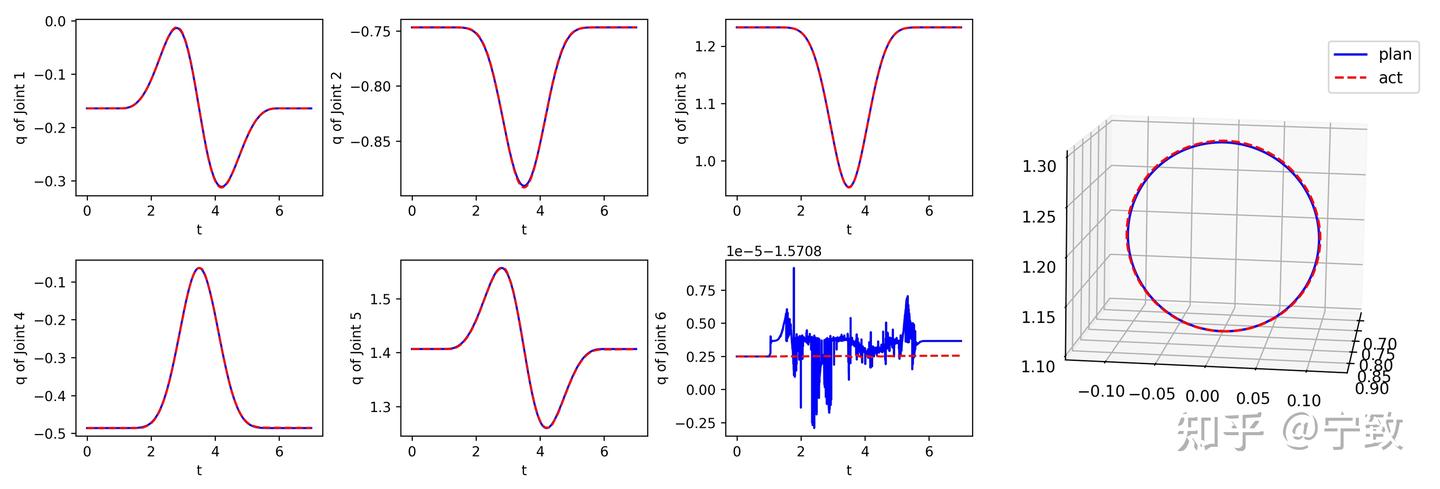
可以看出，跟踪效果显著增强，仔细观察可以看到微小的跟踪误差。表明增加重力补偿，可以在低速运动时达到较为理想的跟踪效果。

进一步地，增加动力学前馈，在RobotModel类中增加逆动力学功能：

def inverse_dynamics(self, q, qd, qdd):
    self.data.qpos = q.copy()
    self.data.qvel = qd.copy()
    self.data.qacc = qdd.copy()
    mujoco.mj_inverse(self.model, self.data)
    tau = self.data.qfrc_inverse
    return tau

在仿真主循环中，修改控制命令：

tau_ref = robot_model.inverse_dynamics(q[step], qd[step], qdd[step])
data.ctrl = robot_controller.update_with_feedforward(data.qpos, data.qvel, q[step], qd[step], tau_ref)

即可实现PD反馈控制+动力学补偿的跟踪效果（PD参数不变）：

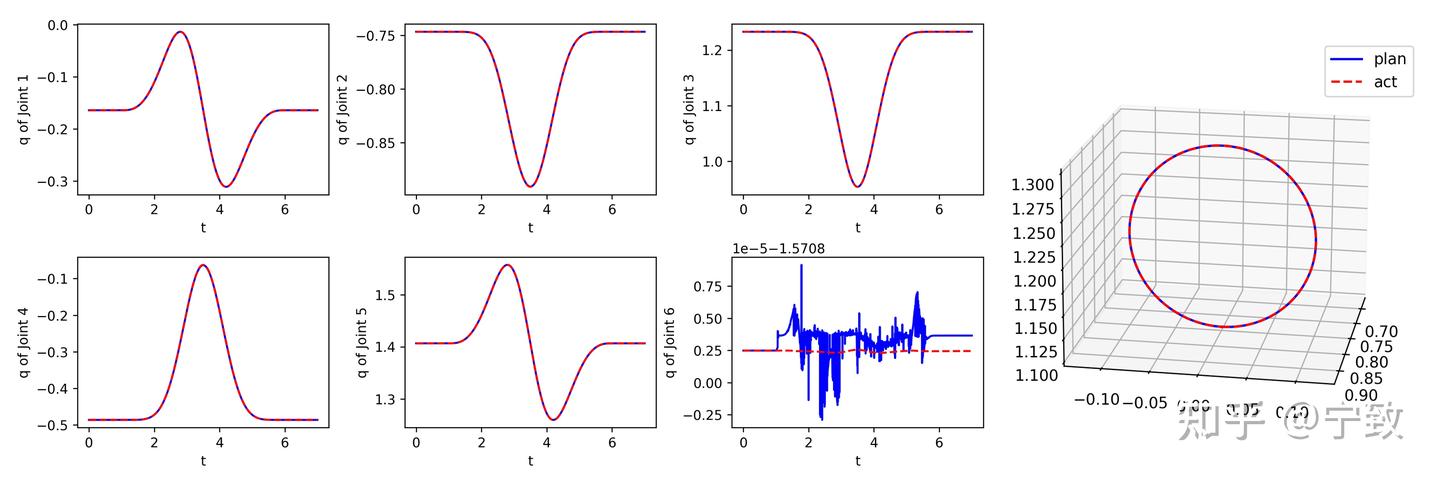
可以看出，跟踪效果进一步增强，几乎看不到跟踪误差了。

定量对比上面三种控制方法的误差：

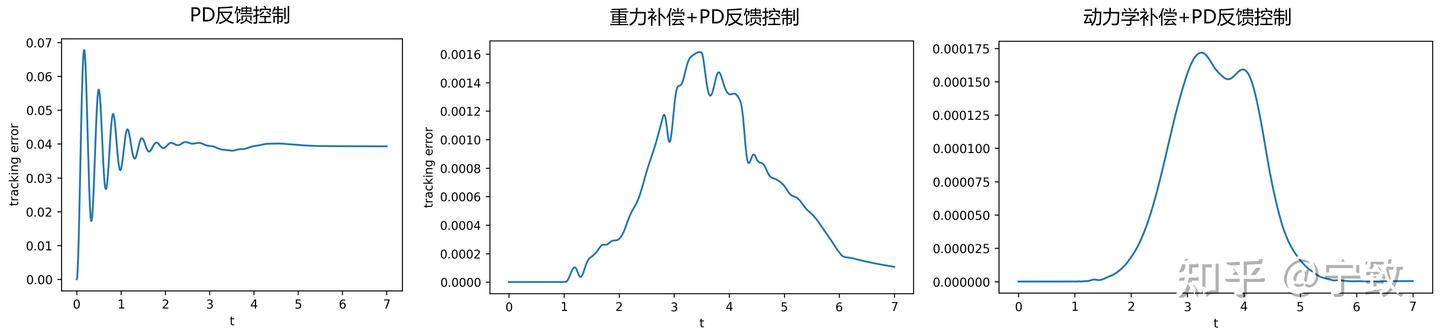
可以看出，机械臂末端跟踪误差在只有关节PD闭环控制时，有厘米级的误差（当然调优PD参数可以减小误差），但增加了重力补偿后，误差降低到1mm左右。进一步增加动力学前馈后，误差减小到0.1mm左右。

2.3 不同速度下的误差对比

前面提到了在速度较低时，只采用重力补偿就可以达到较好的跟踪效果。顺便就对比一下不同速度下的跟踪效果（横轴表示完成圆周用的时间）：

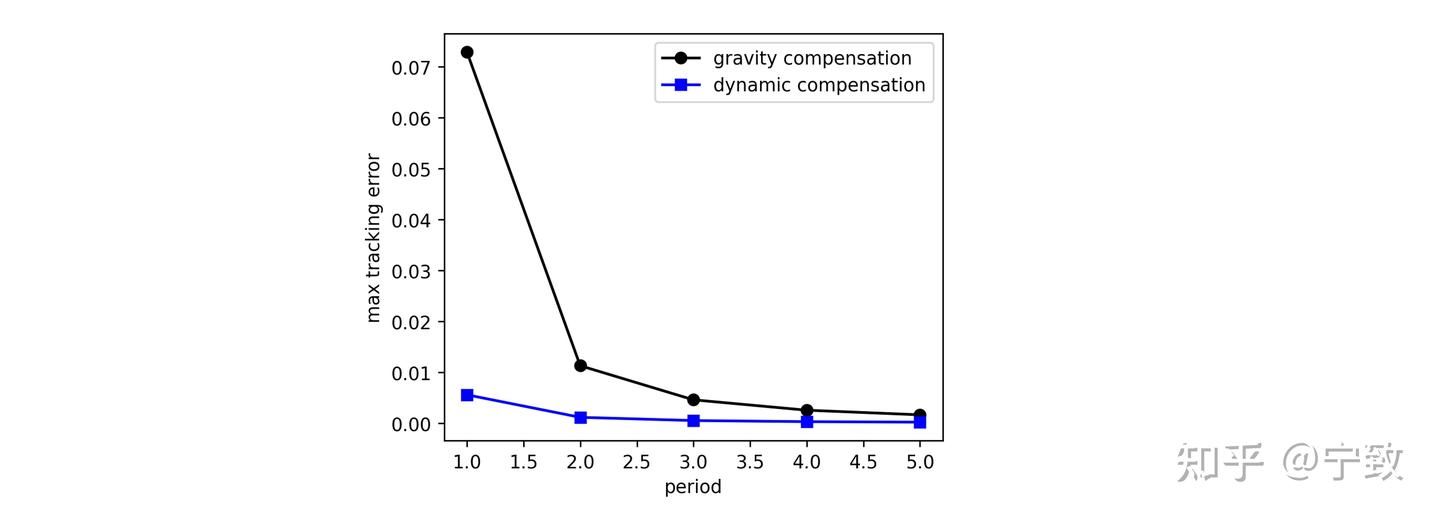
可以看出重力补偿在高速时，跟踪效果显著降低。而动力学补偿在速度增大的情况下，虽然跟踪效果也有所降低，但降低的趋势有限。

在仿真中显然模型是准确的，导致动力学补偿在速度增大时跟踪效果变差的原因主要是控制频率不变，速度升高后，离散化的数值误差增大导致的。

最后，值得一提的是，关节空间的位置控制是最直接的。但最大的问题是，需要逆运动学求解。通常情况下逆运动学求解是数值解，计算复杂度高，且容易出现跳变（尤其是接近奇异点，或接近关节运动边界时）。

赏 0

猜你喜欢

灵巧手常见的传动方案都有哪些？
学习

来源：https://www.zhihu.com/question/1960299903910650751/answer/196030378238...
1周前 33
机器人动力学库哪个更好？
学习

来源：https://www.zhihu.com/question/437857717/answer/1897953312235586570 ...
2周前 22
机器人灵巧手的关节怎么设计？
学习

来源：https://www.zhihu.com/question/27944838/answer/1953754270240335673 ...
3周前 37
马斯克说，人形机器人最难的不是大脑，而是灵巧手和量产。灵巧手为何那么难？
学习

来源：https://www.zhihu.com/question/1950897949698668255/answer/196256666940...
3周前 84
1350元入门具身智能-lerobot机械臂
学习

来源：https://zhuanlan.zhihu.com/p/1895609105902704289 前段时间一直在看具...
4周前 28
机械臂完成长程多步骤的组装任务
学习

来源：https://zhuanlan.zhihu.com/p/16403276747 FMB: a Functional Manipula...
4周前 34

评论0

取消

没有账号？注册  忘记密码？