机械臂的控制（二）

来源：https://zhuanlan.zhihu.com/p/1947982685357217203

本篇为第二部分，末端执行器笛卡尔空间的位置跟踪控制方法。

根据《机器人学导论》第三版（John Craig等）的机械臂控制章节，总结机械臂控制方法。并以UR5机械臂为例，在MUJOCO仿真中执行一个末端圆形轨迹，以对比不同方法的效果。

代码仓库：github.com/DrNingZhi/robot_sim

3. 笛卡尔空间的位置控制

在前面部分中，需要将末端运动轨迹，转化为关节空间运动轨迹，需要对整个轨迹求解逆运动学，计算复杂度高。本篇主要讨论直接进行笛卡尔空间的控制。

3.1 笛卡尔空间的直接控制方法-逆雅可比控制

逆雅可比控制：期望末端位姿和反馈的实际位置的差异，乘以雅可比的逆，转化为关节角度差异，然后通过增益控制器，得到关节驱动力。

�=��⋅�−1[��−��(�)]

注意到，这里的末端位姿偏差（认为很小），被当作期望减小偏差所需要的末端速度，因此通过逆雅可比矩阵转化为关节速度。这里的kp的size仍然等于自由度，和关节对应。

末端位姿应该是6d的，用6d向量表示姿态，书中没有具体讲应该怎么处理，如果用XYZ+欧拉角表示，那么这里的角速度就是欧拉角速度，可能不对。这里我的看法是，要对应角速度，应该将期望姿态和实际姿态的偏差，转化为轴角表示。

首先，将上述控制律分解为位置和姿态

�=��⋅�−1[��−���]

其中，w表示姿态偏差的轴角，首先获得偏差的旋转矩阵。然后可通过Rodrigues公式的逆计算轴角（见《机器人学导论》或《仿人机器人》相关章节）。可以直接利用现有的库实现。然而，需要注意的是，由于R是从当前姿态到目标姿态的旋转，因此得到的w是相对当前姿态坐标系的，需要再转到世界坐标系（需要注意！）

�=�����,

�=��⋅������(�)

显然，上面的控制率没有包含速度反馈。虽然书中指出可以添加速度反馈，但并未明确如何添加，按照我的理解，应该是：

�=��⋅�−1[��−��(�)]+��⋅�−1(�˙�−��˙)

针对这一控制方法的代码实现：

class RobotJacInvController:
    def __init__(self, kp, kd, robot_model, ee_body_name, ee_point_on_body):
        self.kp = kp
        self.kd = kd
        self.robot_model = robot_model
        self.ee_body_name = ee_body_name
        self.ee_point_on_body = ee_point_on_body

    def update(self, q, qd, pos_ref, rotmat_ref, vel_ref, angvel_ref):
        pos, rotmat = self.robot_model.forward_kinematics(
            q, self.ee_body_name, self.ee_point_on_body
        )
        jac = self.robot_model.jacobian(q, self.ee_body_name, self.ee_point_on_body)

        p = pos_ref - pos
        R = rotmat.T @ rotmat_ref
        w = rotmat @ Rotation.from_matrix(R).as_rotvec()
        pos_err = np.hstack((p, w))
        q_err = np.linalg.pinv(jac) @ pos_err

        ee_vel_ref = np.hstack(vel_ref, angvel_ref)
        vel_err = ee_vel_ref - jac @ qd
        qd_err = np.linalg.pinv(jac) @ vel_err
        tau = self.kp * q_err + self.kd * qd_err
        return tau

修改mujoco的仿真主循环

import numpy as np
import mujoco
import mujoco.viewer
from scipy.spatial.transform import Rotation

mjcf_file = "ur5/ur5.xml"
model = mujoco.MjModel.from_xml_path(mjcf_file)
data = mujoco.MjData(model)
dt = model.opt.timestep
dof = model.nv
robot_model = RobotModel(mjcf_file)

center = np.array([0.8, 0.0, 1.2])
radius = 0.1
rotation = Rotation.from_rotvec([0.0, np.pi / 2, 0.0]).as_matrix()
period = 5.0
t, pos, vel, acc = circular_trajectory(center, radius, rotation, dt, period) # 不需要执行ik，计算耗时显著降低。

# Initialize joint states
target = np.eye(4)
target[:3, :3] = rotation
target[:3, 3] = pos[0]
q0 = robot_model.inverse_kinematics(
    target, "wrist_3_link", point_at_body=np.array([0, 0, 0.05]), smooth=False)
data.qpos = q0
data.qvel = np.zeros(dof)

# Initialize controller
kp = np.array([1000.0, 1000.0, 1000.0, 10.0, 10.0, 0.1])
kd = np.array([10.0, 10.0, 10.0, 0.1, 0.1, 0.001])
robot_controller = RobotJacInvController(
    kp, kd, robot_model, "wrist_3_link", np.array([0, 0, 0.05])
)

step = 0
with mujoco.viewer.launch_passive(model, data) as viewer:
    while viewer.is_running() and step < len(t):
        data.ctrl = robot_controller.update(
            data.qpos, data.qvel, pos[step], orientation, vel[step], np.zeros(3)
        )
        mujoco.mj_step(model, data)
        viewer.sync()
        step = step + 1

可以得到开篇视频的仿真结果。可以注意到，kp和kd参数用回和前面关节pd控制相同。有趣的是，跟踪效果也和关节pd控制是相似的：

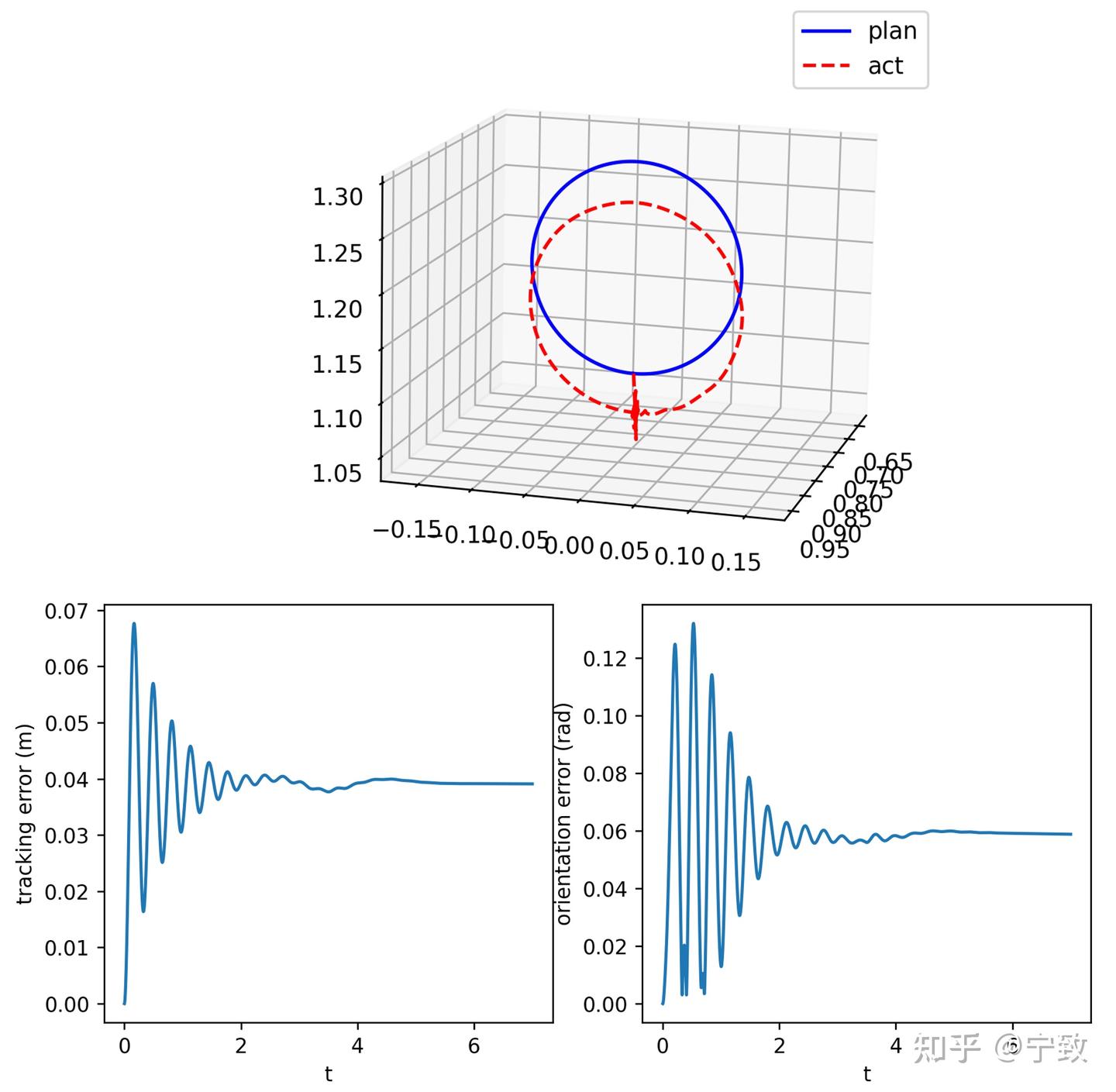
证明两种方法是等效的，但笛卡尔空间控制方法，避免了求整条轨迹的逆运动学，计算复杂度显著降低。

3.2 笛卡尔空间的直接控制方法-转置雅可比控制

虽然上面的方法避免了全轨迹的逆运动学，但一般情况下，求矩阵的逆也是较为复杂的运算。尤其大多数情况下jacobian矩阵不是方阵，只能求解伪逆，精度显著降低。而转置雅可比控制可以避免求雅可比矩阵的逆。

转置雅可比控制：期望末端位姿和反馈的实际位置的差异，通过增益控制器，得到等效末端驱动力。然后乘以雅可比的转置，转化为关节驱动力。

�=���=��{��[��−��(�)]+��[�˙�−��˙]}

这里的pd参数是空间6d对应的pd参数，不再是关节对应的pd参数。虽然书中也没有明确如何添加速度反馈，但这里的速度反馈是明确的。

控制方法的代码实现：

class RobotJacTController:
    def __init__(self, kp, kd, robot_model, ee_body_name, ee_point_on_body):
        self.kp = kp
        self.kd = kd
        self.robot_model = robot_model
        self.ee_body_name = ee_body_name
        self.ee_point_on_body = ee_point_on_body

    def update(self, q, qd, pos_ref, rotmat_ref, vel_ref, angvel_ref):
        pos, rotmat = self.robot_model.forward_kinematics(
            q, self.ee_body_name, self.ee_point_on_body
        )
        jac = self.robot_model.jacobian(q, self.ee_body_name, self.ee_point_on_body)

        p = pos_ref - pos
        R = rotmat.T @ rotmat_ref
        w = rotmat @ Rotation.from_matrix(R).as_rotvec()
        pos_err = np.hstack((p, w))

        ee_vel_ref = np.hstack((vel_ref, angvel_ref))
        vel_err = ee_vel_ref - jac @ qd

        tau = jac.T @ (self.kp * pos_err + self.kd * vel_err)
        return tau

在mujoco仿真主循环中，修改kp和kd为末端六维值，进行控制器初始化：

kp = np.array([2000.0, 2000.0, 5000.0, 100.0, 100.0, 100.0])
kd = np.array([20.0, 20.0, 50.0, 1.0, 1.0, 1.0])
robot_controller = RobotJacTController(
    kp, kd, robot_model, "wrist_3_link", np.array([0, 0, 0.05])
)

跟踪效果也和关节pd控制是相似的，但这种方法不仅避免了全轨迹的逆运动学，而且避免了jacobian矩阵求逆。因此计算复杂度显著提升。

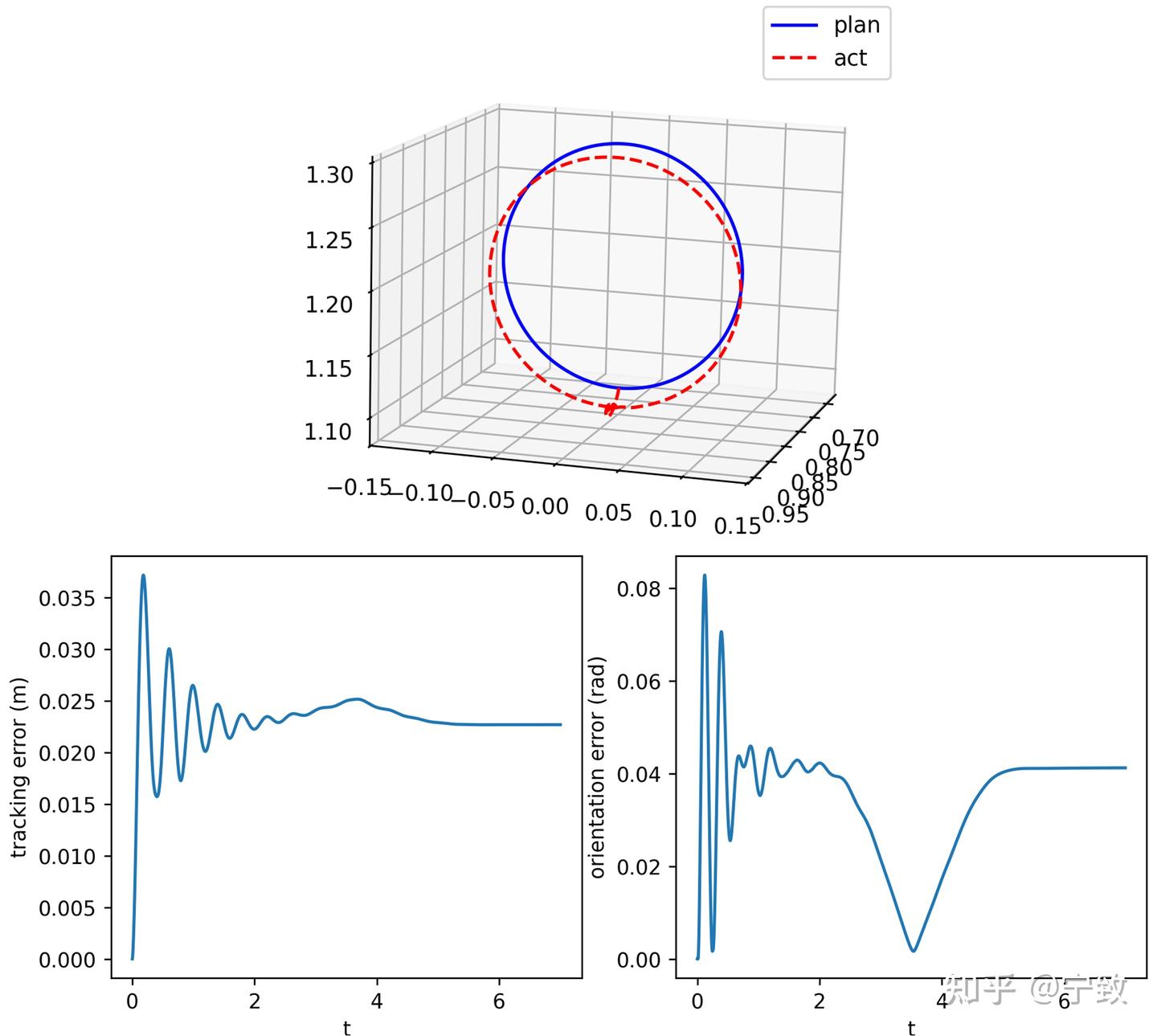
虽然进一步优化PD参数可以提升效果。上面两种方法和关节PD控制一样，不是精确的控制方法，难以保证不同位姿下的效果。

3.3 笛卡尔空间的解耦控制方法

这一方法本质上是笛卡尔空间直接控制+动力学前馈的方法，即

�=��{��+��[��−��(�)]+��[�˙�−��˙]}

其中，

��=�−���

关节空间的前馈扭矩，需要从末端笛卡尔空间量求逆运动学获得，比较复杂，因此，可以通过雅可比进行简化：

首先，

��=�(�)�¨+�(�,�˙)+�(�)+�(�,�˙)

��=��(�)�¨�+��(�,�˙)+��(�)+��(�,�˙)

有

��=�−�[�(�)�¨+�(�,�˙)+�(�)+�(�,�˙)]

由于 �˙=��˙,�¨=�˙�˙+��¨

�¨=�−1(�¨−�˙�˙)

有

��=�−��(�)�−1�¨−�−��(�)�−1�˙�˙+�−�[�(�,�˙)+�(�)+�(�,�˙)]

因此， ��(�)=�−��(�)�−1,��(�,�˙)=�−�[�(�,�˙)−�(�)�−1�˙�˙],��(�)=�−��(�),��(�,�˙)=�−��(�,�˙),

然而，上面的推导仍不能解决问题。要计算前馈力，仍然需要期望关节位置和速度（需要逆运动学）。

虽然可以用当前的实际状态获取，但那就不需要前面的推导，直接利用关节空间逆动力学来计算关节扭矩即可。这个方法本质上相当于一种0力控制，或许可行。因此，我假设

�=��{��[��−��(�)]+��[�˙�−��˙]}+��

测试这个方法是否可行，我假设只考虑重力补偿，用当前实际关节角计算重力补偿作为tau_d。

实现很简单，在前面的RobotJacTController控制器类的update函数最后，增加

tau_ref = self.robot_model.gravity_torque(q)
tau += tau_ref

即可实现：

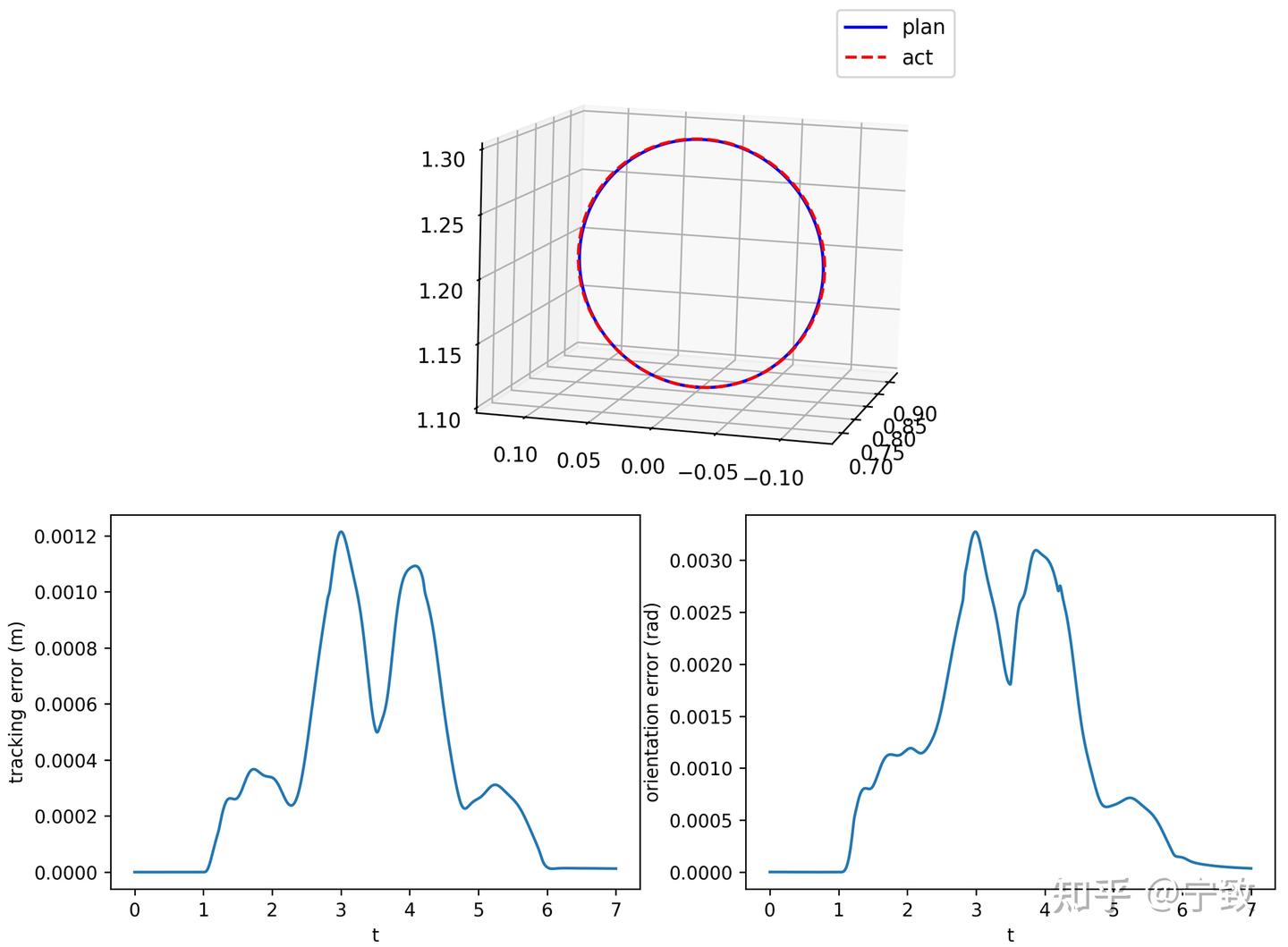
可以看出，跟踪效果显著增强，仔细观察可以看到微小的跟踪误差。和关节空间控制+重力补偿的效果接近。表明重力补偿采用实际关节状态也是可行的。这实际上应该称作零重力控制+笛卡尔空间直接控制方法。然而，如果是基于当前关节空间状态的动力学前馈，控制系统就不稳定了。

事实上，书中提供的动力学前馈方法是：

�=���

其中， �=��(�){�¨�+��[��−��(�)]+��(�˙�−��˙)}+��(�,�˙)+��(�)+��(�,�˙)

所有的关节状态都采用实际状态计算。结合上面的推导，可以简化为 �=�(�)�−1{�¨�+��[��−��(�)]+��(�˙�−��˙)}−�(�)�−1�˙�˙+�(�,�˙)+�(�)+�(�,�˙)

需要计算M矩阵，在RobotModel类中添加功能：

def inertia_matrix(self, q):
    self.data.qpos = q.copy()
    mujoco.mj_step(self.model, self.data)
    M_matrix = np.zeros((self.dof, self.dof))
    mujoco.mj_fullM(self.model, M_matrix, self.data.qM)
    return M_matrix

在RobotJacTController类中增加控制器的实现：

def update_with_feedforward(self, q, qd, pos_ref, rotmat_ref, vel_ref, angvel_ref, acc_ref, angacc_ref):
    M = self.robot_model.inertia_matrix(q)
    jac = self.robot_model.jacobian(q, self.ee_body_name, self.ee_point_on_body)
    jac_inv = np.linalg.pinv(jac)
    jac_d = self.robot_model.jacobian_d(
        q, qd, self.ee_body_name, self.ee_point_on_body
    )
    jac_T_inv = np.linalg.pinv(jac.T)
    tau_compensation = self.robot_model.inverse_dynamics(
        q, qd, np.zeros(self.robot_model.dof)
    )
    pos, rotmat = self.robot_model.forward_kinematics(
        q, self.ee_body_name, self.ee_point_on_body
    )

    p = pos_ref - pos
    R = rotmat.T @ rotmat_ref
    w = rotmat @ Rotation.from_matrix(R).as_rotvec()
    pos_err = np.hstack((p, w))

    ee_vel_ref = np.hstack((vel_ref, angvel_ref))
    vel_err = ee_vel_ref - jac @ qd

    acc_d = np.hstack((acc_ref, angacc_ref))
    xdd_correction = self.kp * pos_err + self.kd * vel_err
    tau = (
        M @ jac_inv @ (acc_d + xdd_correction)
        - M @ jac_inv @ jac_d @ qd
        + tau_compensation
    )
    return tau

在mujoco仿真中修改控制器的调用为

data.ctrl = robot_controller.update_with_feedforward(
    data.qpos,
    data.qvel,
    pos[step],
    orientation,
    vel[step],
    np.zeros(3),
    acc[step],
    np.zeros(3),
)

即可实现：

可以看出，跟踪效果显著增强，跟踪误差极小。

至此，《机器人学导论》中最基础的位置控制方法已经学习完毕。后续继续探讨力控、和其他更高级的位置控制方法。